Xác định yếu tố song song giữa đường và mặt
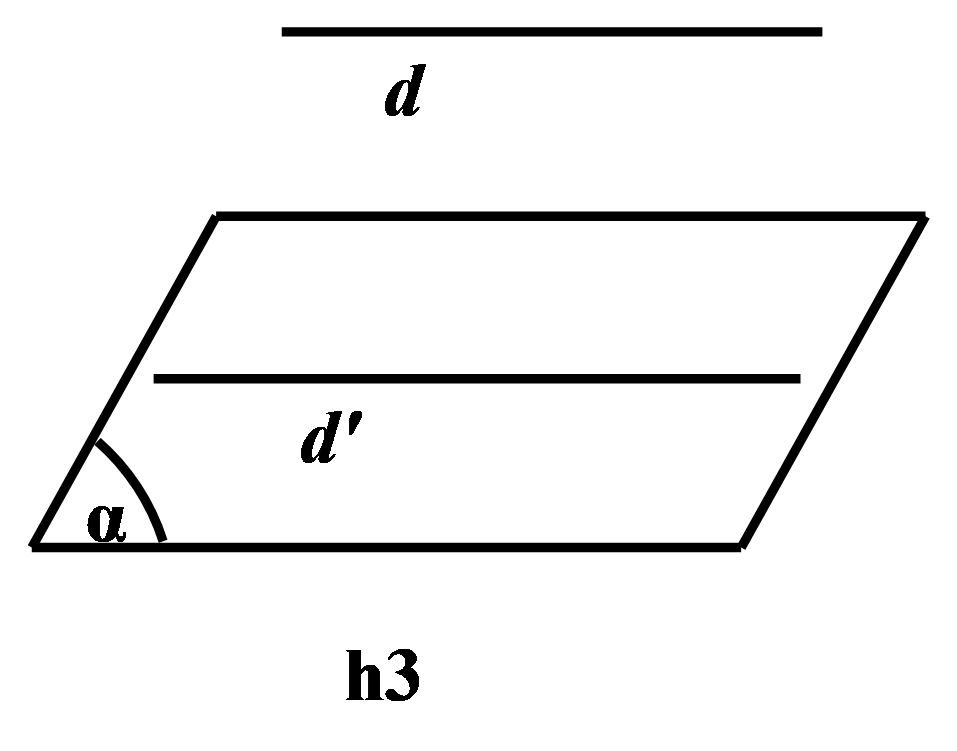
Lý thuyết về Xác định yếu tố song song giữa đường và mặt
Phương pháp chứng minh đường thẳng song song với mặt phẳng
Để chứng minh đường thẳng dd songsong với mặt phẳng (α)(α) ta chứng minh dd song song với một đường thẳng d′ nằm trong (α).
Ví dụ: Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng có tâm lần lượt là O và O′.
a) Chứng minh OO′ song song với các mặt phẳng (ADF) và (BCE).
b) Gọi M,N lần lượt là hai điểm trên các cạnh AE,BD sao cho AM=13AE,BN=13BD. Chứng minh MN song song với (CDEF).
Lời giải:
a) Ta có OO′ là đường trung bình của tam giác BDF ứng với cạnh DF nên OO′∥DF, DF⊂(ADF)
⇒OO′∥(ADF).
Tương tự, OO′ là đường trung bình của tam giác ACE ứng với cạnh CE nên OO′∥CE, CE⊂(CBE)⇒OO′∥(BCE).
b) Trong (ABCD), gọi I=AN∩CD
Do AB∥CD nên ANAI=BNBD⇒ANAI=13.
Lại có AMAE=13⇒ANAI=AMAE⇒MN∥IE. Mà I∈CD⇒IE⊂(CDEF)⇒MN∥(CDEF).
Bài tập tự luyện có đáp án
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G1,G2 lần lượt là trọng tâm tam giác ABC và SBC. Khi đó ta có
- A
- B
- C
- D

Gọi I là trung điểm của BC
Vì G1,G2 lần lượt là trọng tâm tam giác ABC và SBC nên ta có
IG1IA=IG2IS(=13)
Theo định lí Ta-lét đảo ta có G1G2//AS⊂(SAB), G1G2⊄(SAB) ⇒G1G2//(SAB).
Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J lần lượt là trung điểm của AB và CD. Giao tuyến của hai mp(SAB và (SCD) là đường thẳng song song với:
- A
- B
- C
- D
Do 2 mp (SAB) và (SCD) có chung điểm S là lần lượt đi qua hai đương thẳng song song AB và CD nên chúng cắt nhau theo giao tuyến đi qua S và song song với AB và CD ⇒ Giao tuyến của hai mp(SAB và (SCD) là đường thẳng song song với BI.
Câu 3: Cho tứ diện ABCD, gọi M, N lần lượt là trung điểm các cạnh AB và AC. Khi đó vị trí tương đối của đường thẳng MN và mp(BCD) là
- A
- B
- C
- D
⇒MN//BC
Ta có {MN⊄(BCD)MN//BCBC⊂(BCD)⇒MN//(BCD)
Câu 4: Cho hình chóp tứ giác S.ABCD. Goi d là giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng d:
- A
- B
- C
- D
Áp dụng định lý về giao tuyến của 3 mặt phẳng (SAB) và (SCD) và (ABCD)
Câu 5: Cho tứ diện ABCD, gọi M,K lần lượt là trung điểm của BC,AC,N là điểm trên cạnh BD sao cho BN=2ND. Gọi F là giao điểm của AD và (MNK). Khẳng định nào sau đây là đúng?
- A
- B
- C
- D
Ta tìm giao tuyến của mp(ABD) và mp(MNK).
+ N∈(ABD)∩(MNK)
+MK//AB ( do MK là đường trung bình của tam giác ABC)
+MK⊂(MNK), AB⊂(ABC)
Suy ra giao tuyến của mp(ABD) và mp(MNK) là đường thẳng x qua N và song song với AB và MK, x cắt AD tại F. Khi đó F=AD∩(MNK).
Do đó NF//AB, theo định lý Ta-lét ta có:
AFFD=BNND=2 hay AF=2FD.
Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng (SAD) và (SBC). Khẳng định nào sau đây là khẳng định đúng?
- A
- B
- C
- D
Do (SAD) và (SBC) có điểm chung là S. mà AD//BC nên giao tuyến cần xác định là d qua S và song song với BC
Câu 7: Cho hình chóp S.ABCD có ABCD là hình bình hành. Gọi e là giao tuyến của (SAB) và (SCD). Tìm e ?
- A
- B
- C
- D
Do 2 mp (SAB) và (SCD) có chung điểm S là lần lượt đi qua hai đương thẳng song song AB và CD nên chúng cắt nhau theo giao tuyến đi qua S và song song với AB và CD →e=Sx là đường thẳng song song với AB và CD.
Câu 8: Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Kết luận nào dưới đây là không đúng
- A
- B
- C
- D
+ Đáp án "AB//mp(SCD)": ta có {AB⊄(SCD)AB//CDCD⊂(SCD)
⇒AB//(SCD)
Do đó kết luận A là đúng.ss
+ Đáp án "BC//mp(SAD)" tương tự {BC⊄(SAD)BC//ADAD⊂(SAD)⇒BC//mp(SAD) Suy ra kết luận B đúng.
+ Đáp án "SC//mp(ABCD)" ta thấy C là điểm chung của đường thẳng SC và mp(ABCD), theo định nghĩa đường thẳng song song với mặt phẳng suy ra kết luận C không đúng.
+ Đáp án "(SCD)∩(ABCD)=CD.": dễ thấy C và D là 2 điểm chung của 2 mp(SCD) và (ABCD). Do đó (SCD)∩(ABCD)=CD. Vậy kết luận D là đúng.
Lưu ý ở đây đề bài yêu cầu tìm kết luận không đúng, vậy nên đáp án của câu hỏi này là đáp án C.
Câu 9: Cho hình chóp S.ABCD có đáy là tứ giác lồi, O là giao điểm hai đường chéo. Gọi (α) là mặt phẳng qua O và song song với SC, cắt AS tại G. Khi đó ta có
- A
- B
- C
- D
SC//(α)SC⊂(SAC)(α)∩(SAC)=a}⇒a//SC
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M,N,P lần lượt là trung điểm của AB,DC,SA. Khi đó số giao điểm của SC và mp(MNP) là
- A
- B
- C
- D
PQ//MNvì cùng song song với AD. Ta có
P∈(MNP)PQ//MN}⇒Q∈(MNP)⇒QN⊂(MNP) (2)
Mà SC⊄(MNP) (3)
Từ (1) (2) và (3) suy ra SC//(NMP) nên số giao điểm của chúng là 0.
Câu 11: Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của (SAB) và (SCD) là
- A
- B
- C
- D

Vì AB//CD ⇒ Giao tuyến của (SAB) và (SCD) là đường thẳng đi qua S và song song với AB.
Xem thêm các bài tiếp theo bên dưới