Diện tích hình bình hành, hình thoi
Lý thuyết về Diện tích hình bình hành, hình thoi
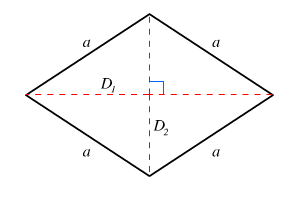
Công thức tính diện tích hình thoi
+ Diện tích hình thoi bằng tích của một cạnh với chiều cao ứng với cạnh đó.
+ Diện tích hình thoi bằng một nửa tích 2 đường chéo
S=D1D22S=D1D22
Công thức tính diện tích hình bình hành
Diện tích hình bình hành bằng tích của một cạnh với chiều cao ứng với cạnh đó.
S=ahS=ah
Bài tập tự luyện có đáp án
Câu 1: Hình thoi có độ dài hai đường chéo là 6cm6cm và 8cm8cm . Tính độ dài đường cao của hình thoi.
- A
- B
- C
- D
Giả sử hình thoi ABCDABCD , đường chéo ACAC vuông góc với BDBD tại OO , AC=8cm;BD=6cmAC=8cm;BD=6cm
Gọi BHBH là đường cao hình thoi kẻ từ đỉnh BB .
Ta có: DO=12BD=12.6=3(cm);AO=12AC=12.8=4(cm)DO=12BD=12.6=3(cm);AO=12AC=12.8=4(cm)
Áp dụng định lí Py-ta-go trong tam giác vuông AODAOD vuông tại OO ta có:
AD=√AO2+OD2=√42+32=5(cm)SABCD=12BD.AC=12.6.8=24(cm2)SABCD=BH.AD⇒BH=SABCDAD=245=4,8(cm).
Câu 2: Cho hình chữ nhật ABCD , có diện tích S=20cm2 . Gọi M,N,P,Q lần lượt là các trung điểm AB,BC,CD,AD . Khi đó diện tích MNPQ bằng
- A
- B
- C
- D

Ta có MN;NP;PQ;PM đều là đường trung bình nên MN=NP=PQ=PM bằng 12 đường chéo ABCD .
Khi đó MNPQ là hình thoi
⇒SMNPQ=12MP.NQ=12S=10cm2
Câu 3: Cạnh của một hình thoi ABCD bằng 13, một đường chéo DB bằng 12. Đường chéo còn lại bằng
- A
- B
- C
- D

Gọi giao điểm AC và BD là O
Ta có BO=BD2=122=6 cm
Áp dụng định lý pi – ta – go vào trong tam giác vuông ABO⇒AO=√AB2−OB2=√132−62=√133
⇒AC=2√133
Câu 4: Gọi d1;d2 là độ dài 2 đường chéo của hình thoi. Công thức diện tích hình thoi theo độ dài 2 đường chéo là
- A
- B
- C
- D
Xét hình thoi ABCD, khi đó có 2 đường chéo AC;BD vuông góc với nhau
Nên ta có
SABCD=SABC+SBDA=12BO.AC+12DO.AC=12(BO+DO).AB=12BD.AB=d1d22
Câu 5: Cho hình thoi ABCD có cạnh dài 6cm và ˆA=300 . Khi đó diện tích hình thoi bằng
- A
- B
- C
- D

Từ B kẻ BH⊥AD(H∈AD)
Tam giác vuông AHB là một nửa tam giác đều ABE (E là điểm đối xứn của B qua H) nên:
BH=12AB=3(cm)
Vậy SABCD=BH.AD=3.6=18(cm2)
Câu 6: Hình thoi ABCD có góc A=600 . Trên cạnh AD lấy điểm M, trên canh CD lấy điểm N sao cho AM=DN .
- A
- B
- C
- D

Có góc ˆA=600;AB=AD⇒ tam giác ABD là tam giác đều
Xét 2 tam giác AMB và DBM ta có
AB=BDAM=DN^BAM=^BDN}⇒△AMB=△DBM⇒{BM=BN(1)^ABM=^DBN
Mặt khác ta có ^ABM+^MBD=600⇒^NBD+^MBD=600(2)
Từ (1),(2)⇒△MBN là tam giác đều
Câu 7: Hai đường chéo hình thoi ABCD có độ dài là BD=16cm và AC=12cm. Chu vi hình thoi bằng
- A
- B
- C
- D

Gọi O là giao điểm 2 đường chéo. Ta có
BO=BD2=162=8OC=AC2=122=6⇒BC=√BO2+OC2=10
Vậy chu vi hình thoi bằng: 10.4=40cm
Câu 8: Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Gọi E, F, G, H theo thứ tự là chân Các đường vuông góc kẻ từ O đến AB, BC, CD, DA. Tứ giác EFGH là hình
- A
- B
- C
- D

Ta có: AB//CD(gt)OE⊥AB(gt)}⇒OE⊥CD
Mặt khác OG⊥CD(gt)⇒OE≡OG nên ba điểm O,E,G thẳng hàng.
BC//AD(gt)OF⊥BC(gt)}⇒OF⊥AD
Mà OH⊥AD(gt) ⇒OF≡OH nên ba điểm O,H,F thẳng hàng.
Vì AC và BD là đường phân giác các góc của hình thoi nên:
OE=OF ; OE=OH ; OH=OG
Tứ giác EFGH có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên nó là hình chữ nhật.
Câu 9: Cho hình chữ nhật ABCD có diện tích là S1 . Vẽ tứ giác MNPQ có các đỉnh là trung điểm các cạnh của hình chữ nhật và SMNPQ=S2 . Khi đó mối quan hệ giữa S1;S2 là
- A
- B
- C
- D

Ta có SABCD=AB.BC=NQ.MP
Các tam giác BMN,CNP,DPQ,AMQ bằng nhau nên MN=NP=PQ=QM
Suy ra, MNPQ là hình thoi ⇒SMNPQ=NQ.MP2=SABCD2
⇒S2=S12⇔2S2=S1
Câu 10: Cho hình thang cân ABCD(AB//CD). Gọi E,F,G,H theo thứ tự là trung điểm của các cạnh AB,BC,CD,DA.
- A
- B
- C
- D

+ Trong ΔABD ta có: EA=EB;HA=HD ⇒EH là đường trung bình của ΔABD
⇒EH//BD;EH=12BD (1)
+ Trong ΔCBD ta có: FB=FC;GC=GD⇒FG là đường trung bình của ΔCBD
⇒FG//BD;FG=12BD (2)
Từ (1) và (2) suy ra: EH//FG;EH=FG
Suy ra: Tứ giác EFGH là hình bình hành
Trong ΔABC ta có: EF là đường trung bình ⇒EF=12AC (3); AC=BD (4)
Từ (1), (3) và (4) suy ra: EH=EF⇒ tứ giác EFGH là hình thoi.
Câu 11: Cho hình thoi có cạnh là 5cm , một trong hai đường chéo có độ dài là 6cm . Diện tích của hình thoi là
- A
- B
- C
- D
Giả sử hình thoi ABCD , đường chéo AC vuông góc với BD tại O
BO=12BD=12.6=3(cm)
Áp dụng định lí Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
AO=√AB2−OB2=√52−32=4
SABCD=12BD.AC=12BD.2AO=BD.AO=6.4=24(cm2) .
Câu 12: Cho hình thoi ABCD, biết AB=5cm,AI=4cm (I là giao điểm của hai đường chéo). Diện tích hình thoi là
- A
- B
- C
- D

Áp dụng Pi-ta-go vào tam giác vuông IAB, ta có: AB2=AI2+IB2
⇒IB2=AB2−AI2=25−16=9
⇒IB=3(cm)
AC=2AI=2.4=8(cm)
BD=2IB=2.3=6(cm)
SABCD=12AC.BD=12.6.8=24(cm2)
Câu 13: Cho hình thoi ABCD có cạnh dài 4cm và ˆA=600 . Khi đó diện tích hình thoi bằng
- A
- B
- C
- D

Ta có AD=AB;ˆA=600⇒△ABD là tam giác đều
Khi đó AB=BD=4;AO=AB√32=2√3
⇒SABCD=AC.BD2=8√3(cm2)
Câu 14: Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O . Biết AB=10cm,OA=6cm . Diện tích hình thoi ABCD là
- A
- B
- C
- D
Áp dụng định lí Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO=√AB2−OA2=√102−62=8cm SABCD=12BD.AC=122.BO.2AO=2BO.AO=2.8.6=96(cm2) .