Các đại lượng đặc trưng của dòng điện xoay chiều
Lý thuyết về Các đại lượng đặc trưng của dòng điện xoay chiều
1. Khái niệm
Dòng điện xoay chiều hình sin, gọi tắt là dòng điện xoay chiều, là dòng điện có cường độ biến thiên tuần hoàn với thời gian theo quy luật của hàm sin hay cos, với dạng tổng quát:
$i={{I}_{0}}cos(\omega t+{{\varphi }_{i}})$
Trong đó: i là giá trị cường độ dòng điện tại thời điểm t, được gọi là giá trị tức thời của i ( cường độ tức thời).
- ${{I}_{0}}>0$ được gọi là giá trị cực đại của i ( cường độ cực đại)
- $\omega >0$ được gọi là tần số góc, $T=\dfrac{2\pi }{\omega }$ là chu kì và $f=\dfrac{\omega }{2\pi }$ là tần số của i. Ở Việt Nam mạng điện xoay chiều dân dụng có tần số f=50Hz
- $\alpha =\left( \omega t+\varphi \right)$ là pha của i và $\varphi $ là pha ban đầu
2. Điện áp xoay chiều
Khi 2 đầu khung dây chưa nối với tải điện thì HĐT là suất điện động, người ta gọi HĐT dao động điều hòa là HĐT xoay chiều hoặc điện áp xoay chiều và có biểu thức:
$u={{U}_{0}}cos(\omega t+{{\varphi }_{u}})$
Trong đó:
u là HĐT tức thời 2 đầu đoạn mạch.
${{U}_{o}}$là HĐT cực đại 2 đầu đoạn mạch.
$\omega $ là tần số góc.(rad/s)
${{\varphi }_{u}}$ là pha ban đầu của HĐT 2 đầu đoạn mạch.
3. Độ lệch pha phụ thuộc vào tính chất mạch điện ( chứa các linh kiện gì, mắc như thế nào) nhưng không phụ thuộc vào tần số dòng điện.
Với $\varphi ={{\varphi }_{u}}-{{\varphi }_{i}}$ là độ lệch pha của u so với i, có $-\dfrac{\pi }{2}\le \varphi \le \dfrac{\pi }{2}$
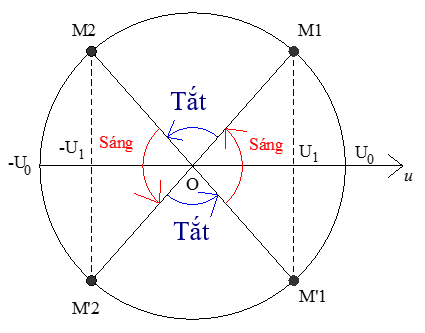
4. Thời gian đèn sáng, tắt trong 1 chu kì
Khi đặt điện áp $u={{U}_{0}}cos(\omega t+{{\varphi }_{u}})$ vào hai đầu bóng đèn, biết đèn chỉ sáng lên khi $u\ge {{U}_{1}}.$
$\Delta t=\dfrac{4\Delta \varphi }{\omega }$ Với $c\text{os}\Delta \varphi =\dfrac{{{U}_{1}}}{{{U}_{0}}}$, $(0<\Delta \varphi <\pi /2)$
Chú ý: Có thể dụng dụng những khoảng thời gian đặc biệt tương tự như dao động cơ.
5. Xác định thời gian, thời điểm
Giả sử cường độ dòng điện xoay chiều: $i={{I}_{0}}\cos \left( \omega t+\varphi \right)$
Xác định thời điểm vật có cường độ $i=k{{I}_{0}}$ ( k là hệ số tỉ lệ) kể từ thời điểm ban đầu.
+ Thời điểm ban đầu: t=0$\Rightarrow \left\{ \begin{align}& i={{I}_{0}}\cos \varphi \\ & \sin \varphi ? \\ \end{align} \right.$ ( tại thời điểm $t\ne 0$ làm tương tự)
+ Sử dụng mối liên hệ giữa chuyển động tròn đều và dao động điều hòa $\left( \Delta \varphi =\omega .\Delta t \right)$
VD: Cho phương trình cường độ dòng điện: $i=5\cos \left( 100\pi t+\dfrac{\pi }{2} \right)\left( A \right)$ Xác định thời điểm đầu tiên có cường độ dòng điện là 2,5A.
HD:
Tại thời điểm ban đầu: $t=0\Rightarrow \left\{ \begin{align}& i=5\cos \dfrac{\pi }{2}=0 \\ & \sin \dfrac{\pi }{2}>0 \\ \end{align} \right.\Rightarrow $ i=0 và đang giảm.
Kể từ thời điểm ban đầu đến lần đầu tiên có cường độ dòng điện là 2,5A, thì trong chuyển động tròn đều quét được góc
$\Delta \varphi =\pi +\dfrac{\pi }{6}=\omega .\Delta t\Leftrightarrow \dfrac{7\pi }{6}=100\pi .\Delta t\Rightarrow \Delta t=\dfrac{7}{600}\left( s \right)$
Sử dụng các khoảng thời gian đặc biệt:
$T=\dfrac{2\pi }{\omega }=\dfrac{1}{50}\left( s \right)$
Kể từ thời điểm ban đầu đến thời điểm i=2,5A. $\left( 0\to -{{I}_{0}}\to \dfrac{{{I}_{0}}}{2} \right)$
$\Rightarrow \Delta t=\dfrac{T}{4}+\dfrac{T}{4}+\dfrac{T}{12}=\dfrac{7T}{12}=\dfrac{7}{600}\left( s \right)$
Bài tập tự luyện có đáp án
Câu 1: Tại thời điểm t = 1,5s cường độ dòng điện trong mạch có giá trị ℓà i = 5A. Giá trị trên ℓà giá trị:
- A
- B
- C
- D
Giá trị cường độ dòng điện tại một thời điểm nào đó gọi là giá trị tức thời
Câu 2: Một dòng điện chạy trong một đoạn mạch có cường độ$i=4cos\left( 2\pi ft+\dfrac{\pi }{2} \right)$ (A) (f > 0). Đại lượng f được gọi là
- A
- B
- C
- D
Tần số của dòng điện xoay chiều là f.
Câu 3: Dòng điện xoay chiều qua một đoạn mạch có cường độ $i=4\cos \dfrac{2\pi t}{T}(A)$(T>0). Đại lượng T được gọi là
- A
- B
- C
- D
T là chu kì của dòng điện xoay chiều.
Câu 4: Mắc ampe kế nhiệt xoay chiều nối tiếp với một đoạn mạch thì thấy ampe kế chỉ 1 A. Cường độ dòng điện cực đại của đoạn mạch này là
- A
- B
- C
- D
Chỉ số của ampe kế nhiệt cho biết giá trị hiệu dụng của cường độ dòng điện trong mạch.
Cường độ dòng điện cực đại $ {{I}_{0}}=\sqrt{2}I=\sqrt{2} $ A
Câu 5: Một dòng điện có phương trình $ i=2\cos 100\pi t(A) $ . Giá trị hiệu dụng của dòng điện là
- A
- B
- C
- D
Giá trị hiệu dụng của dòng điện là: $ \sqrt{2}A $
Câu 6: Dòng điện chạy qua một đoạn mạch có cường độ biến thiên điều hòa theo thời gian. Đại lượng T được gọi là.
- A
- B
- C
- D
Đại lượng T là chu kì của dòng điện
Câu 7: Tìm phát biểu đúng về dòng điện xoay chiều?
- A
- B
- C
- D
Dòng điện xoay chiều là dòng điện có:
+mchiều biến thiên tuần hoàn theo thời gian.
+cường độ dòng điện biến thiên điều hòa theo thời gian.
Câu 8: Ở nước ta, mạng điện dân dụng sử dụng điện áp
- A
- B
- C
- D
Mạng điện dân dụng ở nước ta sử dụng điện áp xoay chiều có giá trị hiệu dụng $ U=220V $
Câu 9: Biểu thức cường độ dòng điện trong đoạn mạch xoay chiều là $ i=2\cos \left( 100\pi t \right)\left( A \right) $ . Tần số của dòng điện là bao nhiêu?
- A
- B
- C
- D
Tần số của dòng điện: $ f=\dfrac{\omega }{2\pi }=\dfrac{100\pi }{2\pi }=50Hz $
Câu 10: Điện áp tức thời giữa hai đầu một đoạn mạch điện xoay chiều có biểu thức $ u=220\sqrt{2}\cos 100\pi t\left( V \right) $ . Điện áp hiệu dụng giữa hai đầu một mạch điện là:
- A
- B
- C
- D
Điện áp hiệu dụng: $ U=\dfrac{{{U}_{0}}}{\sqrt{2}}=\dfrac{220\sqrt{2}}{\sqrt{2}}=220V $
Xem thêm các bài tiếp theo bên dưới