Pha ban đầu của biên độ tổng hợp
Lưu về Facebook:
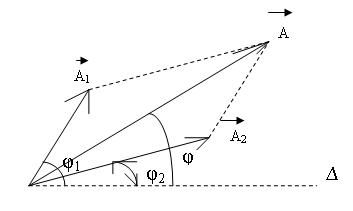
Lý thuyết về Pha ban đầu của biên độ tổng hợp
x1;x2 là phương trình dao động thành phần và x là phương trình dao động tổng hợp.
x1=A1cos(ωt+φ1)x2=A2cos(ωt+φ2)}⇒x=Acos(ωt+φ)
tanφ=A1sinφ1+A2sinφ2A1cosφ1+A2cosφ2
Bài tập tự luyện có đáp án
Câu 1: Chọn câu đúng. Một vật thực hiện đồng thời hai dao động điều hoà có phương trình dao động x1=A1.cos(ωt+φ1) và x2=A2.cos(ωt+φ2). Pha ban đầu của dao động tổng hợp được xác định
- A
- B
- C
- D
Dùng giản đồ vecto để tổng hợp hai dao động điều hòa cùng phương, cùng tần số.
ta có góc lệch
tgφ=AyAx=A1.sinφ1+A2.sinφ2A1.cosφ1+A2.cosφ2

Câu 2: Hai dao động điều hòa cùng phương, cùng tần số có biên độ và pha ban đầu lần lượt là A1,φ1 vàA2,φ2. Dao động tổng hợp của hai dao động này có pha ban đầu φ được tính theo công thức
- A
- B
- C
- D
tanφ=A1sinφ1+A2sinφ2A1cosφ1+A2cosφ2
Xem thêm các bài tiếp theo bên dưới