Các định nghĩa, tính chất
Lý thuyết về Các định nghĩa, tính chất
Định nghĩa 1
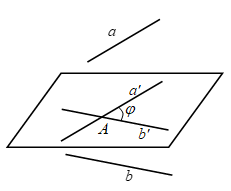
Góc giữa hai đường thẳng \[a\] và \[b\] trong không gian là góc giữa hai đường thẳng \[{a}'\] và \[{b}'\] cùng đi qua một điểm bất kì và lần lượt song song với \[a\] và \[b\]. Ta có: \[\left( a,b \right)=\left( {a}',{b}' \right)=\varphi \]
Định nghĩa 2
Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng \[{{90}^{0}}\].
Kí hiệu: \[a\bot b\] hay \[b\bot a\].
Nhận xét.
+) Nếu $\vec{u}$, $\vec{v}$ lần lượt là vectơ chỉ phương của hai đường thẳng \[a\] và \[b\] thì \[a\bot b\Leftrightarrow \vec{u}.\vec{v}=0\].
+) Nếu \[\left\{ \begin{array}{l}
a{\rm{// }}b\\
c \bot a
\end{array} \right. \Rightarrow c \bot b\]
Bài tập tự luyện có đáp án
Câu 1: Cho $\alpha $ là góc tạo bởi hai đường thẳng $\left( {{d}_{1}} \right)$ và $\left( {{d}_{2}} \right)$. Khẳng định nào sau đây là đúng ?
- A
- B
- C
- D
Góc giữa đường thẳng và đường thẳng luôn nằm trong đoạn ${{0}^{0}}\le \alpha \le {{90}^{0}}$
Câu 2: Trong các mệnh đề sau mệnh đề nào đúng?
- A
- B
- C
- D
Định nghĩa: Góc giữa hai đường thẳng $a$ và $b$ bằng góc giữa hai đường thẳng $a$ và $c$ khi $b$ song song với $c$ (hoặc $b$ trùng với $c$).