Liên hệ giữa dây và khoảng cách từ tâm đến dây trong đường tròn
Lý thuyết về Liên hệ giữa dây và khoảng cách từ tâm đến dây trong đường tròn
Định lý 1:
Trong một đường tròn:
a) Hai dây bằng nhau thì cách đều tâm.
b) Hai dây cách đều tâm thì bằng nhau.
Định lý 2:
Trong hai dây của một đường tròn:
a) Dây nào lớn hơn thì dây đó gần tâm hơn.
b) Dây nào gần tâm hơn thì dây đó lớn hơn.
Bài tập tự luyện có đáp án
Câu 1: Cho đường tròn (O;R)(O;R) có hai dây AB,CDAB,CD vuông góc với nhau ở MM . Biết AB=16cm;CD=12cm;MC=2cmAB=16cm;CD=12cm;MC=2cm . Khoảng cách từ tâm OO đến dây ABAB là
- A
- B
- C
- D
Xét đường tròn tâm (O)(O) .
Kẻ OE⊥ABOE⊥AB tại EE suy ra EE là trung điểm của ABAB , kẻ OF⊥CDOF⊥CD tại FF suy ra FF là trung điểm của CDCD .
Xét tứ giác OEMFOEMF có ˆE=ˆF=ˆM=90∘ˆE=ˆF=ˆM=90∘ nên OEIFOEIF là hình chữ nhật, suy ra FM=OEFM=OE .
Ta có CD=12cm⇒FC=6cmCD=12cm⇒FC=6cm mà MC=2cm⇒FM=FC−MC=4cmMC=2cm⇒FM=FC−MC=4cm nên OE=4cmOE=4cm
Vậy khoảng cách từ tâm OO đến dây ABAB là 4cm4cm .
Câu 2: Cho đường tròn (O)(O) , dây cung ABAB và CDCD với CD=ABCD=AB . Giao điểm KK của các đường thẳng ABAB và CDCD nằm ngoài đường tròn. Vẽ đường tròn (O;OK)(O;OK) , đường tròn này cắt KAKA và KCKC lần lượt tại MM và NN . So sánh KMKM và KNKN .
- A
- B
- C
- D
Xét đường tròn (O;OB)(O;OB)
Kẻ OE⊥CD;OF⊥ABOE⊥CD;OF⊥AB tại E,FE,F mà CD<AB⇒OE>OFCD<AB⇒OE>OF (hai dây bằng nhau thì cách đều tâm)
Xét đường tròn (O;OK)(O;OK) có OE⊥KN;OF⊥KMOE⊥KN;OF⊥KM tại E,FE,F mà OE=OF⇒KN=KMOE=OF⇒KN=KM (liên hệ giữa dây và khoảng cách từ tâm đến dây)
Câu 3: Cho đường tròn tâm OO bán kính 25cm25cm , dây AB=40cmAB=40cm . Vẽ dây CDCD song song với ABAB và có khoảng cách đến ABAB bằng 22cm22cm . Độ dài dây CDCD là
- A
- B
- C
- D
TH1: AB và CD khác phía với O
Hạ OH⊥AB;OK⊥CD
Ta có OH=15⇒OK=7⇒CD=2KD=2√252−72=48
TH2: AB và CD cùng phía với O (loại vì khi đó OK=37 >22
Câu 4: Cho đường tròn (O) bán kính bằng 3cm . Một đường thẳng đi qua điểm A nằm bên ngoài đường tròn và cắt đường tròn tại B và C, trong đó AB=BC . Kẻ đường kính COD . Tính độ dài AD .
- A
- B
- C
- D
Trong tam giác ACD , ta có :
B là trung điểm của AC(gt);O là trung điểm của CD
Nên OB là đường trung bình của ΔACD .
Suy ra : OB=12AD (tính chất đường trung bình của tam giác)
Vậy AD=2.OB=2.3=6(cm)
Câu 5: Cho đường tròn (O;15cm) , dây AB=24cm . Một tiếp tuyến song song với AB cắt các tia OA,OB theo thứ tự E,F . Độ dài EF bằng
- A
- B
- C
- D

Gọi C là tiếp điểm của EF với đường tròn (O), H là giao điểm của OC và AB.
Ta có OC⊥EF và AB//EF nên OC⊥AB
Ta tính được HB = 12 cm nên OH = 9 cm.
Ta có tam giác ΔOAB∼ΔOEF⇒OHOC=ABEF⇒EF=40cm
Câu 6: Cho hình thang vuông ABCD vuông tại A và D,AB=4cm,BC=13cm,CD=9cm . Độ dài đoạn AD bằng
- A
- B
- C
- D

Kẻ BE⊥CD
Suy ra tứ giác ABED là hình chữ nhật
Ta có: AD=BE ; AB=DE=4(cm)
Suy ra: CE=CD−DE=9−4=5(cm)
Áp dụng định lí Pitago vào tam giác vuông BCE ta có :
BC2=BE2+CE2 ⇒BE2=BC2−CE2=132−52=144
⇒BE=12(cm)
Vậy: AD=12(cm)
Câu 7: Cho đường tròn (O) , đường kính AB . Lấy điểm C là trung điểm đoạn OB . Kẻ dây MN qua C và dây AD//MN . So sánh độ dài AD và MN .
- A
- B
- C
- D
Kẻ đường thẳng qua O vuông góc với AC tại E và cắt BD tại F thì EF⊥BD tại F vì AC//BD .
Xét hai tam giác vuông OEA và tam giác OFB có ^AEO=^OFC=90∘;^AOE=^FOC (đối đỉnh)
Nên ΔAEO∼ΔCFO (g - g) ⇒OEOF=OAOC mà OA=OB=2.OC⇒OEOF=OAOC=2⇒OE=2OF
Hay OE>OF suy ra AD<MN (dây nào xa tâm hơn thì dây đó nhỏ hơn).
Câu 8: Cho đường tròn (O) bán kính 13cm , dây AB bằng 24cm . Khoảng cách từ O đến dây AB bằng
- A
- B
- C
- D
Kẻ OH⊥AB,H∈AB
Dễ thấy ΔOAB cân tại O.
Do đó, OH vừa là đường cao, trung tuyến của tam giác
⇒H là trung điểm của AB⇒HA=HB=3 cm.
OH2=OB2−HB2=52−32=42. Do đó OH=4 cm
Câu 9: Cho đường tròn (O) và hai dây AB , CD . Biết CD=24cm và cách O một đoạn 9cm. Tính độ dài dây AB biết khoảng cách từ O đến AB là 10cm .
- A
- B
- C
- D
Gọi H,K lần lượt là trung điểm của CD và AB
Suy ra OH⊥CD;OK⊥AB và OH=9cm; OK=10cm.
Tam giác OHC vuông tại H nên OC2=OH2+HC2=92+122=225⇒OA2=OC2=225 .
Tam giác OAK vuông tại K nên AK2=OA2−OK2=225−102=125⇒AK=5√5(cm).
Vậy AB=2AK=10√5(cm) .
Câu 10: Cho đoạn thẳng AB. Đường tròn (O) đường kính 4cm tiếp xúc với đường thẳng AB. Tập hợp tâm O nằm trên
- A
- B
- C
- D
Ta có O luôn cách AB 1 khoảng cách bằng bán kính tức bằng 2cm
Khi đó tập hợp các tâm O thỏa mãn là 2 đường thẳng song song với AB và cách AB 1 khoảng bằng 2cm
Câu 11: Chọn khẳng định sai. Cho đường tròn (O) có AB là đường kính. Vẽ hai dây AD và BC song song nhau.
- A
- B
- C
- D
ABCD là hình chữ nhật nên AD=BC .
DC là đường chéo hcn nên DC=AB⇒DC là đường kính (O)
Câu 12: Cho đường tròn (O;10cm) . Dây AB và CD song song, có độ dài lần lượt là 16cm và 12cm . Tính khoảng cách giữa hai dây.
- A
- B
- C
- D
Kẻ đường thẳng qua O vuông góc với CD tại E và cắt AB tại F thì EF⊥AB vì AB//CD .
Khi đó E là trung điểm của CD và F là trung điểm của AB (đường kính vuông góc với dây thì đi qua trung điểm dây đó)
Nên ED=6cm;FB=8cm;OD=OB=10cm
Áp dụng định lý Pytago cho tam giác vuông OED ta được OE=√OD2−ED2=8cm .
Áp dụng định lý Pytago cho tam giác vuông OFB ta được OF=√OB2−FB2=6cm .
Vậy khoảng cách giữa hai dây là EF=OE+OF=14cm .
Câu 13: Cho đường tròn (O;R) , R=4cm . vẽ dây cung AB=5cm , C là điểm trên dây cung AB sao cho AC=2cm . Vẽ CD vuông góc với OA tại D . Tính độ dài đoạn thẳng AD .
- A
- B
- C
- D
Vẽ đường kính có AE=8cm .
Điểm B thuộc đường tròn đường kính AE ⇒^ABE=900 .
Xét ΔADC và ΔABE có
^DAC (chung),
^ADC=^ABE(=900) ,
do đó ΔADC∼ΔABE ⇒ADAB=ACAE⇒AD=AC.ABAE . Mà AC=2cm,AB=5cm,AE=8cm , nên AD=2.58=54(cm) .
Câu 14: Cho đường tròn (O) bán kính OA=11cm . Điểm M thuộc bán kính AO và cách O khoảng 7cm . Qua M kẻ dây CD có độ dài 18cm . Độ dài các đoạn thẳng MC,MD lần lượt là
- A
- B
- C
- D
Kẻ OE vuông góc CD nên E là trung điểm của đoạn CD⇒CE=ED=CD2=9cm .
Xét ΔCOE vuông tại E ta có OC2=CE2+EO2 ( theo định lí pytago) ⇒OE=√OC2−CE2=√112−92=2√10 .
Tương tự áp dụng định lí pytago trong ΔMOE vuông tại E ta được ME=√MO2−EO2=√72−(2√10)2=3 .
Mà EC=MC+ME⇒MC=ECME=9−3=6⇒MD=CD−MC=18−6=12cm .
Câu 15: Cho đường tròn (O;3cm) , điểm A di chuyển trên đường tròn. Trên tiếp tuyến tại A, lấy điểm M sao cho AM = OA. Điểm M chuyển động trên đường nào?
- A
- B
- C
- D

Xét tam giác vuông AOM có OA=AM=3cm⇒OM=3√2cm
Vậy điểm M chuyển động trên đường tròn (O;3√2cm)
Câu 16: Cho điểm A cách đường thẳng xy là 12cm . Vẽ đường tròn (A;13cm) . Khi đó khẳng định nào sau đây là đúng
Khi đó khẳng định nào sau đây là đúng
- A
- B
- C
- D
Kẻ AH⊥xy , ta có: AH=12cm
Bán kính đường tròn tâm A là R=13cm . Mà AH=d=12cm ⇒d<R
Vậy (A;13cm) cắt đường thẳng xy tại hai điểm phân biệt B và C
Áp dụng định lí Pitago vào tam giác vuông AHC ta có:
AC2=AH2+HC2 ⇒HC2=AC2−AH2=132−122=25⇒HC=5(cm)
Ta có: BC=2.HC=2.5=10(cm)
Câu 17: Chọn khẳng định đúng. Cho đường tròn (O;R) từ điểm M bên ngoài đường tròn ta kẻ hai đường thẳng lần lượt cắt đường tròn tại các điểm A,B và C,D biết AB=CD .
Cho đường tròn (O;R) từ điểm M bên ngoài đường tròn ta kẻ hai đường thẳng lần lượt cắt đường tròn tại các điểm A,B và C,D biết AB=CD .
- A
- B
- C
- D
Vẽ OH⊥AB(H∈AB) , OK⊥CD(K∈CD) .
Ta có AB=CD (gt), nên OH=OK (định lý liên hệ dây cung và khoảng cách đến tâm) và H,K
lần lượt là trung điểm của AB,CD (định lý đường kính vuông góc dây cung) ⇒AH=CK .
Xét ΔOHM (^OHM=900) có OM (cạnh chung) và OH=OK , do đó ΔOHM=ΔOKM (cạnh huyền, cạnh góc vuông) ⇒MH=MK . Ta có MH−AH=MK−CK⇒MA=MC .
Câu 18: Cho đường tròn (O;R) có hai dây AB,CD vuông góc với nhau ở M . Biết CD=8cm;MC=1cm . Khoảng cách từ tâm O đến dây AB là
- A
- B
- C
- D
Xét đường tròn tâm (O) .
Kẻ OE⊥AB tại E suy ra E là trung điểm của AB , kẻ OF⊥CD tại F suy ra F là trung điểm của CD .
Xét tứ giác OEMF có ˆE=ˆF=ˆM=90∘ nên OEIF là hình chữ nhật, suy ra FM=OE .
Ta có CD=8cm⇒FC=4cm mà MC=1cm⇒FM=FC−MC=4−1=3cm nên OE=FM=3cm
Vậy khoảng cách từ tâm O đến dây AB là 3cm .
Câu 19: Cho đường tròn (O) bán kính 50cm và hai dây AB,CD song song với nhau (điểm O không nằm trong phần mặt phẳng giới hạn bởi hai đường thẳng AB và CD ). Biết AB=80cm , CD=96cm . Tính khoảng cách giữa hai dây AB và CD .
- A
- B
- C
- D
Từ O kẻ OE⊥AB=E,OF⊥CD=F .
mà AB//CD nên O,F,E thẳng hàng.
+) Xét tam giác OAE vuông tại E, theo định lý Pytago ta có:
OE2=OA2−AE2=502−402=302⇒OE=30
+)Xét tam giác OCF vuông tại F, theo định lý Pytago ta có OF2=OC2−CF2=502−482=142⇒OF=14(cm).
Khoảng cách giữa hai đường thẳng AB và CD là EF=OE−OF=30−14=16(cm)
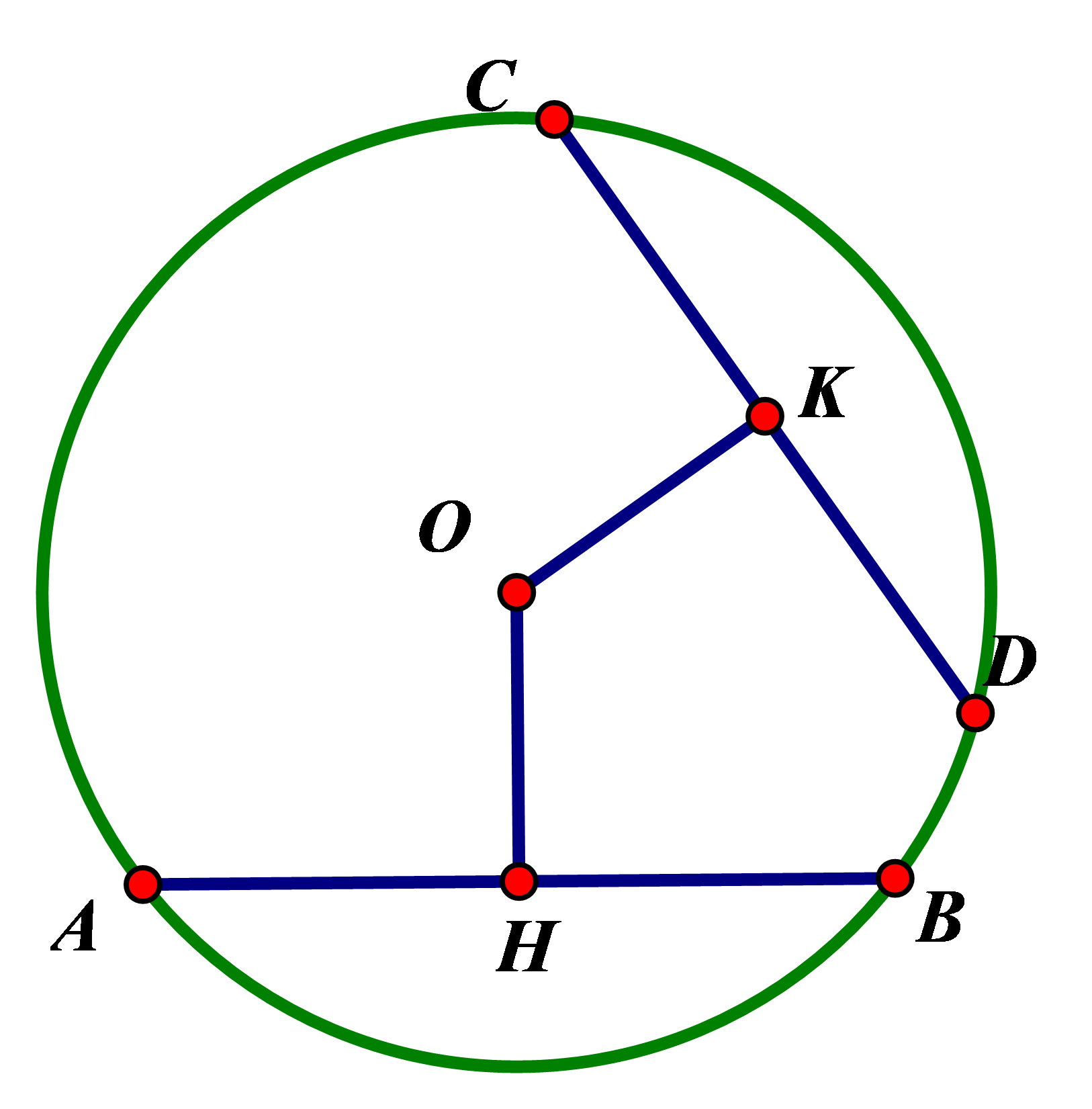
Câu 20: Cho đường tròn (O) , dây cung AB và CD với CD<AB . Giao điểm K của các đường thẳng AB và CD nằm ngoài đường tròn. Vẽ đường tròn (O;OK) , đường tròn này cắt KA và KC lần lượt tại M và N . So sánh KM và KN .
- A
- B
- C
- D
Xét đường tròn (O;OB)
Kẻ OE⊥CD;OF⊥AB tại E,F mà CD<AB⇒OE>OF (dây nào lớn hơn thì gần tâm hơn)
Xét đường tròn (O;OK) có OE⊥KN;OF⊥KM tại E,F mà OE>OF⇒KN<KM (liên hệ giữa dây và khoảng cách từ tâm đến dây)