Sự biến thiên hàm số lượng giác

Bài sau

4.7/5

Tác giả: Thầy Tùng

Đăng ngày: 11 Aug 2022

Lưu về Facebook:

Hình minh họa Sự biến thiên hàm số lượng giác

MỤC LỤC

Lý thuyết

Bài tập

Lý thuyết về Sự biến thiên hàm số lượng giác

1. Sự biến thiên hàm số $y=\sin x$

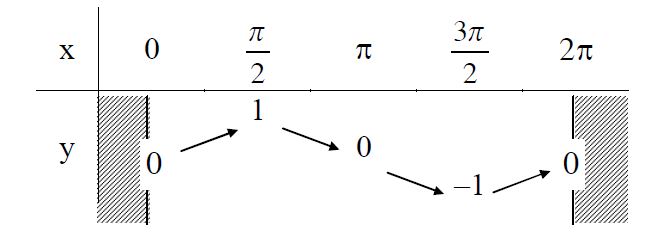
Ta có bảng biến thiên của hàm số $y = \sin{x}$ trên đoạn $[0;2\pi]$ như sau:

$Bảng biến thiên hàm số $y = \sin{x}$$

Hàm số $y = \sin{x}$ nghịch biến trên mỗi khoảng $\left(\dfrac{\pi}{2} + k2\pi;\dfrac{3\pi}{2} + k2\pi\right)$ ; đồng biến trên mỗi khoảng $\left(k2\pi; \dfrac{\pi}{2} + k2\pi\right)$ và mỗi khoảng $\left(\dfrac{3\pi}{2} + k2\pi; 2\pi + k2\pi\right)$ , với mỗi số nguyên $k$ bất kỳ.

2. Sự biến thiên của hàm số $y=\cos x$

Ta có bảng biến thiên của hàm số $y = \cos{x}$ trên đoạn $[0;2\pi]$ như sau:

$Bảng biến thiên hàm số $y = \cos{x}$$

Hàm số $y = \cos{x}$ nghịch biến trên mỗi khoảng $\left(k2\pi;\pi + k2\pi\right)$ ; đồng biến trên mỗi khoảng $\left(\pi + k2\pi; 2\pi + k2\pi\right)$ , với mỗi số nguyên $k$ bất kỳ.

3. Sự biến thiên hàm số $y=\tan x$

Ta có bảng biến thiên của hàm số $y = \tan{x}$ trên khoảng $\left(\dfrac{-\pi}{2};\dfrac{\pi}{2}\right)$ như sau:

$Bảng biến thiên hàm số $y = \tan{x}$$

Hàm số $y = \tan{x}$ đồng biến trên mỗi khoảng $\left(\dfrac{-\pi}{2} + k\pi;\dfrac{\pi}{2} + k\pi\right)$ , với mỗi số nguyên $k$ bất kỳ.

4. Sự biến thiên hàm số $y=\cot x$

Ta có bảng biến thiên của hàm số $y = \cot{x}$ trên khoảng $\left(0;\pi\right)$ như sau:

$Bảng biến thiên hàm số $y = \cot{x}$$

Hàm số $y = \cot{x}$ nghịch biến trên mỗi khoảng $\left(k\pi;(k+1)\pi\right)$ , với mỗi số nguyên $k$ bất kỳ.

Bài sau

Bài tập tự luyện có đáp án

Câu 1: Khẳng định nào sau đây đúng?

A
Hàm số $y=\cos x$ đồng biến trong khoảng $\left( -\dfrac{3\pi } 4 ;-\dfrac{\pi } 4 \right)$ .
B
Hàm số $y=\cos x$ đồng biến trong khoảng $\left( \dfrac{\pi } 4 ;\dfrac{3\pi } 4 \right)$ .
C
Hàm số $y=\sin x$ đồng biến trong khoảng $\left( \dfrac{\pi } 4 ;\dfrac{3\pi } 4 \right)$ .
D
Hàm số $y=\sin x$ đồng biến trong khoảng $\left( -\dfrac{3\pi } 4 ;-\dfrac{\pi } 4 \right)$ .

Bấm vào đây để xem đáp án chi tiết

Do hàm số $y=\cos x$ đồng biến trên $\left( -\pi +k2\pi \,;\,\,k2\pi \right)$ , cho $k=0\Rightarrow \left( -\pi ;0 \right)$

suy ra đồng biến trên $\left( -\dfrac{3\pi } 4 ;-\dfrac{\pi } 4 \right)$ .

Câu 2: Hàm số $y=\cos x$ đồng biến trên đoạn nào dưới đây:

A
$\left[ -\pi ;\pi \right]$ .
B
$\left[ 0;\pi \right]$ .
C
$\left[ \pi ;2\pi \right]$ .
D
$\left[ 0;\dfrac{\pi } 2 \right]$ .

Bấm vào đây để xem đáp án chi tiết

Do hàm số $y=\cos x$ đồng biến trên mỗi khoảng $\left( -\pi +k2\pi \,;\,\,k2\pi \right)$ , cho $k=1\Rightarrow \left( \pi ;2\pi \right)$

Câu 3: Trong các hàm số sau, hàm số nào đồng biến trên khoảng $\left( -\dfrac{\pi }{3};\dfrac{\pi }{6} \right)$

A $y=\tan \left( 2x+\dfrac{\pi }{6} \right)$
B $y=\cot \left( 2x+\dfrac{\pi }{6} \right)$
C $y=\sin \left( 2x+\dfrac{\pi }{6} \right)$
D $y=\cos \left( 2x+\dfrac{\pi }{6} \right)$

Bấm vào đây để xem đáp án chi tiết

Với

$x\in \left( -\dfrac{\pi }{3};\dfrac{\pi }{6} \right)\to 2x\in \left( -\dfrac{2\pi }{3};\dfrac{\pi }{3} \right)\to 2x+\dfrac{\pi }{6}\in \left( -\dfrac{\pi }{2};\dfrac{\pi }{2} \right)$ thuộc góc phần tư thứ IV và thứ I nên hàm số

$y=\sin \left( 2x+\dfrac{\pi }{6} \right)$ đồng biến trên khoảng

$\left( -\dfrac{\pi }{3};\dfrac{\pi }{6} \right)$ .

Câu 4: Cho hàm số $y=\sin 2x$ đồng biến trên khoảng nào trong các khoảng sau?

A $\left( 0;\dfrac{\pi }{4} \right)$
B $\left( \dfrac{\pi }{2};0 \right)$
C $\left( \dfrac{3\pi }{2};2\pi \right)$
D $\left( \pi ;\dfrac{3\pi }{2} \right)$

Bấm vào đây để xem đáp án chi tiết

Xét A. Ta có

$x\in \left( 0;\dfrac{\pi }{4} \right)\to 2x\in \left( 0;\dfrac{\pi }{2} \right)$ thuộc góc phần tư thứ I nên

$y=\sin 2x$ đồng biến trên khoảng này.

Câu 5: Với $x\in \left( 0;\dfrac{\pi }{4} \right)$ , mệnh đề nào sau đây đúng?

AHàm số $y=-\sin 2x$ đồng biến, hàm số $y=-1+\cos 2x$ nghịch biến.
BCả hai hàm số $y=-\sin 2x$ và $y=-1+\cos 2x$ đều nghịch biến.
CCả hai hàm số $y=-\sin 2x$ và $y=-1+\cos 2x$ đều đồng biến.
DHàm số $y=-\sin 2x$ nghịch biến, hàm số $y=-1+\cos 2x$ đồng biến.

Bấm vào đây để xem đáp án chi tiết

Ta có.

$x\in \left( 0;\dfrac{\pi }{4} \right)\to 2x\in \left( 0;\dfrac{\pi }{2} \right)$ thuộc góc phần tư thứ I.

Do đó -

$y=-\sin 2x$ đồng biến

$\xrightarrow{{}}y=-\sin 2x$ nghịch biến. -

$y=\cos 2x$ nghịch biến

$\xrightarrow{{}}y=1-\cos 2x$ nghịch biến.

Câu 6:
Hàm số $y=\sin 2x$ nghịch biến trên khoảng nào sau đây $\left( k\in Z \right)$ .

A $\left( -\dfrac{\pi }{4}+k\pi ;\dfrac{\pi }{4}+k\pi \right)$
B $\left( \dfrac{\pi }{2}+k2\pi ;\dfrac{3\pi }{2}+k2\pi \right)$
C $\left( k2\pi ;\pi +k2\pi \right)$
D $\left( \dfrac{\pi }{4}+k\pi ;\dfrac{3\pi }{4}+k\pi \right)$

Bấm vào đây để xem đáp án chi tiết

Ta thấy hàm số

$y=\sin 2x$ tuần hoàn với chu kì

$T=\dfrac{2\pi }{2}=\pi$ .
Do hàm số

$y=\sin x$ nghịch biến trên

$\left( \dfrac{\pi }{2}+k2\pi ;\dfrac{3\pi }{2}+k2\pi \right),k\in \mathbb{Z}$

$\Rightarrow$ Hàm số

$y=\sin 2x$ nghịch biến khi

$\begin{array}{l} \dfrac{\pi }{2}+k2\pi <2x<\dfrac{3\pi }{2}+k2\pi \\ \Leftrightarrow \dfrac{\pi }{4}+k\pi <x<\dfrac{3\pi }{4}+k\pi ,k\in \mathbb{Z} \end{array}$
Vậy hàm số

$y=\sin 2x$ nghịch biến trên mỗi khoảng

$\left( \dfrac{\pi }{4}+k\pi ;\dfrac{3\pi }{4}+k\pi \right),k\in \mathbb{Z}$

Câu 7: Mệnh đề nào sau đây sai?

A
Hàm số $y=\text{tan}x$ đồng biến trong khoảng $\left( 0;\dfrac{\pi } 2 \right)$ .
B
Hàm số $y=\text{cos}x$ nghịch biến trong khoảng $\left( 0;\dfrac{\pi } 2 \right)$ .
C
Hàm số $y=\text{cot}x$ nghịch biến trong khoảng $\left( 0;\dfrac{\pi } 2 \right)$ .
D
Hàm số $y=\text{sin}x$ đồng biếntrong khoảng $\left( 0;\dfrac{\pi } 2 \right)$ .

Bấm vào đây để xem đáp án chi tiết

Quan sát trên đường tròn lượng giác

trên khoảng $\left( 0;\dfrac{\pi } 2 \right)$ ta thấy: $y=\cos x$ giảm dần.

Câu 8: Cho hàm số $y=sinx$ . Mệnh đề nào sau đây là đúng?

A
Hàm số đồng biến trên khoảng $\left( \dfrac{\pi }{2};\pi \right)$ , nghịch biến trên khoảng $\left( \pi ;\dfrac{3\pi }{2} \right)$ .
B
Hàm số đồng biến trên khoảng $\left( -\dfrac{3\pi }{2};-\dfrac{\pi }{2} \right)$ , nghịch biến trên khoảng $\left( -\dfrac{\pi }{2};\dfrac{\pi }{2} \right)$ .
C
Hàm số đồng biến trên khoảng $\left( -\dfrac{\pi }{2};\dfrac{\pi }{2} \right)$ , nghịch biến trên khoảng $\left( \dfrac{\pi }{2};\dfrac{3\pi }{2} \right)$ .
D
Hàm số đồng biến trên khoảng $\left( 0;\dfrac{\pi }{2} \right)$ , nghịch biến trên khoảng $\left( -\dfrac{\pi }{2};0 \right)$ .

Bấm vào đây để xem đáp án chi tiết

Ta có thể hiểu thể hiểu. “Hàm số

$y=sinx$ đồng biến khi x thuộc góc phần tư thứ IV và thứ I; nghịch biến khi x thuộc góc phần tư thứ II và III”.

Câu 9: Với $x\in \left( \dfrac{31\pi }{4};\dfrac{33\pi }{4} \right)$ , mệnh đề nào sau đây đúng?

A
Hàm số $y=\cot x$ nghịch biến.
B
Hàm số $y=\cos x$ đồng biến.
C
Hàm số $y=tanx$ nghịch biến.
D
Hàm số $y=\sin x$ đồng biến.

Bấm vào đây để xem đáp án chi tiết

Ta có $\left( \dfrac{31\pi }{4};\dfrac{33\pi }{4} \right)=\left( -\dfrac{\pi }{4}+8\pi ;\dfrac{\pi }{4}+8\pi \right)$ thuộc góc phần tư thứ I và II.

Câu 10: Hàm số $y=\tan x$ đồng biến trên khoảng

A
$\left( 0;\dfrac{\pi } 2 \right)$ .
B
$\left( 0;\dfrac{3\pi } 2 \right)$ .
C
$\left( 0;\dfrac{\pi } 2 \right]$ .
D
$\left( -\dfrac{3\pi } 2 ;\dfrac{\pi } 2 \right)$ .

Bấm vào đây để xem đáp án chi tiết

Do hàm số $y=\tan x$ đồng biến trên $\left( 0;\dfrac{\pi } 2 \right)$ .

Câu 11:
Xét hai mệnh đề sau.
(I) Với mọi $x\in \left( -\dfrac{\pi }{2};\dfrac{\pi }{2} \right)$ thì hàm số $y={{\tan }^{2}}x$ là hàm tăng
(II) Với mọi $x\in \left( -\dfrac{\pi }{2};\dfrac{\pi }{2} \right)$ thì hàm số $y={{\sin }^{2}}x$ là hàm tăng
Chọn phương án đúng.

ACả hai sai
BCả hai đúng
CChỉ (II) đúng
DChỉ (I) đúng

Bấm vào đây để xem đáp án chi tiết

Ta thấy cả hai hàm số đều không là hàm tăng trên cả khoảng

$\left( -\dfrac{\pi }{2};\dfrac{\pi }{2} \right).$
Vì khi

$x$ chạy từ

$-\dfrac{\pi }{2}$ đến

$0$ thì giá trị của hai hàm số đều giảm.
Khi

$x$ chạy từ

$0$ đến

$\dfrac{\pi }{2}$ thì giá trị của hai hàm số đều tăng, vậy cả hai mệnh đề đều sai.

Câu 12:
Xét hai mệnh đề sau.
(I) $\forall x\left( \pi ;\dfrac{3\pi }{2} \right)$ . Hàm số $y=\dfrac{1}{\sin x}$ giảm
(II) $\forall x\left( \pi ;\dfrac{3\pi }{2} \right)$ . Hàm số $y=\dfrac{1}{\cos x}$ giảm
Chọn mệnh đề đúng trong các mệnh đề trên

AChỉ (I)
BCả 2 sai
CCả 2 đúng
DChỉ (II)

Bấm vào đây để xem đáp án chi tiết

$\forall x\in \left( \pi ;\dfrac{3\pi }{2} \right);$ Hàm

$y=\sin x$ giảm và

$\operatorname{sinx}<0,\forall x\in \left( \pi ;\dfrac{3\pi }{2} \right),$ suy ra hàm

$y=\dfrac{1}{\operatorname{sinx}}$ tăng;
Câu (I) sai,

$\forall x\in \left( \pi ;\dfrac{3\pi }{2} \right);$ Hàm

$y=\cos x$ tăng và

$\cos x<0;\forall x\in \left( \pi ;\dfrac{3\pi }{2} \right)$ , suy ra hàm

$y=\dfrac{1}{\cos x}$ giảm. Câu (II) đúng.

Câu 13:
Trong khoảng $\left( \dfrac{\pi }{2}+k2\pi ;\pi +k2\pi \right),k\in Z$ thì mệnh đề nào sau đây là sai?

AHàm số $y=\cos x$ là hàm số nghịch biến.
BHàm số $y=\tan x$ là hàm số đồng biến.
CHàm số $y=\cot x$ là hàm số đồng biến.
DHàm số $y=\sin x$ là hàm số nghịch biến.

Bấm vào đây để xem đáp án chi tiết

Thật vậy, với

$\dfrac{2\pi }{3};\dfrac{3\pi }{4}\in \left( \dfrac{\pi }{2};\pi \right)$ , ta có.

$\dfrac{2\pi }{3}<\dfrac{3\pi }{4}\Rightarrow \cot \dfrac{2\pi }{3}=-\dfrac{\sqrt{3}}{3}>-1=\cot \dfrac{3\pi }{4}$

Câu 14: Chọn khẳng định đúng?

A
Hàm số $y=\cos x$ đồng biến trên mỗi khoảng $\left( \dfrac{\pi } 2 +k2\pi ;\pi +k2\pi \right)$ và nghịch biến trên mỗi khoảng $\left( \pi +k2\pi ;k2\pi \right)$ với $k\in \mathbb Z$ .
B
Hàm số $y=\cos x$ đồng biến trên mỗi khoảng $\left( -\pi +k2\pi ;k2\pi \right)$ và nghịch biến trên mỗi khoảng $\left( k2\pi ;\pi +k2\pi \right)$ với $k\in \mathbb Z$ .
C
Hàm số $y=\cos x$ đồng biến trên mỗi khoảng $\left( \dfrac{\pi } 2 +k2\pi ;\dfrac{3\pi } 2 +k2\pi \right)$ và nghịch biến trên mỗi khoảng $\left( -\dfrac{\pi } 2 +k2\pi ;\dfrac{\pi } 2 +k2\pi \right)$ với $k\in \mathbb Z$ .
D
Hàm số $y=\cos x$ đồng biến trên mỗi khoảng $\left( k2\pi ;\pi +k2\pi \right)$ và nghịch biến trên mỗi khoảng $\left( \pi +k2\pi ;3\pi +k2\pi \right)$ với $k\in \mathbb Z$ .

Bấm vào đây để xem đáp án chi tiết

Hàm số $y=\cos x$ đồng biến trên mỗi khoảng $\left( -\pi +k2\pi ;k2\pi \right)$ và nghịch biến trên mỗi khoảng $\left( k2\pi ;\pi +k2\pi \right)$ với $k\in \mathbb Z$ .

Câu 15:
Với $k\in Z,$ kết luận nào sau đây về hàm số $y=\tan 2x$ là sai?

AHàm số $y=\tan 2x$ nhận mỗi đường thẳng $x=\dfrac{\pi }{4}+k\dfrac{\pi }{2}$ làm tiệm cận
BHàm số $y=\tan 2x$ luôn đồng biến trên mỗi khoảng $\left( -\dfrac{\pi }{2}+k\dfrac{\pi }{2};\dfrac{\pi }{2}+k\dfrac{\pi }{2} \right)$
CHàm số $y=\tan 2x$ là hàm số lẻ
DHàm số $y=\tan 2x$ tuần hoàn với chu kỳ $T=\dfrac{\pi }{2}$

Bấm vào đây để xem đáp án chi tiết

Ta thấy hàm số

$y=\tan x$ luôn đồng biến trên mỗi khoảng

$\left( -\dfrac{\pi }{2}+k\pi ;\dfrac{\pi }{2}+k\pi \right)$

$\Rightarrow$ Hàm số

$y=\tan 2x$ luôn đồng biến khi

$-\dfrac{\pi }{2}+k\pi <2x<\dfrac{\pi }{2}+k\pi \Leftrightarrow -\dfrac{\pi }{4}+k\dfrac{\pi }{2}<x<\dfrac{\pi }{4}+k\dfrac{\pi }{2}$
Vậy B sai.

Câu 16:
Để hàm số $y=\sin x+\cos x$ tăng, ta chọn $x$ thuộc khoảng nào?

A $\left( -\dfrac{3\pi }{4}+k\pi ;\dfrac{\pi }{4}+k\pi \right).$
B $\left( -\dfrac{\pi }{2}+k2\pi ;\dfrac{\pi }{2}+k2\pi \right).$
C $\left( \pi +k2\pi ;2\pi +k2\pi \right).$
D $\left( -\dfrac{3\pi }{4}+k2\pi ;\dfrac{\pi }{4}+k2\pi \right).$

Bấm vào đây để xem đáp án chi tiết

Ta có.

$y=\sin x+\cos x=\sqrt{2}\sin \left( x+\dfrac{\pi }{4} \right)$
Để hàm số

$y=\sin x+\cos x$ tăng thì

$\begin{array}{l} -\dfrac{\pi }{2}+k2\pi <x+\dfrac{\pi }{4}<\dfrac{\pi }{2}+k2\pi ;k\in \mathbb{Z} \\ \Leftrightarrow -\dfrac{3\pi }{4}+k2\pi <x<\dfrac{\pi }{4}+k2\pi ;k\in \mathbb{Z}. \end{array}$

Câu 17:
Hàm số $y=\cos 2x$ nghịch biến trên khoảng nào sau đây $\left( k\in Z \right)$

A
$\left( -\dfrac{\pi }{2}+k2\pi ;\dfrac{\pi }{2}+k2\pi \right)$ .
B
$\left( \dfrac{\pi }{2}+k2\pi ;\dfrac{3\pi }{2}+k2\pi \right)$ .
C
$\left( \dfrac{\pi }{2}+k\pi ;\pi +k\pi \right)$ .
D
$\left( k\pi ;\dfrac{\pi }{2}+k\pi \right)$ .

Bấm vào đây để xem đáp án chi tiết

Hàm số $y=\cos 2x$ nghịch biến khi $k2\pi <2x<\pi +k2\pi \Leftrightarrow k\pi <x<\dfrac{\pi }{2}+k\pi ,k\in \mathbb{Z}$ .

Câu 18:
Cho hàm số $y=4\sin \left( x+\dfrac{\pi }{6} \right)\cos \left( x-\dfrac{\pi }{6} \right)-\sin 2x$ . Kết luận nào sau đây là đúng về sự biến thiên của hàm số đã cho?

AHàm số đã cho đồng biến trên $\left( 0;\dfrac{\pi }{4} \right)$ và $\left( \dfrac{1}{4}\pi ;\pi \right)$
BHàm số đã cho đồng biến trên $\left( 0;\pi \right)$
CHàm số đã cho đồng biến trên các khoảng $\left( 0;\dfrac{\pi }{4} \right)$ và $\left( \dfrac{3}{4}\pi ;\pi \right)$
DHàm số đã cho nghịch biến trên khoảng $\left( 0;\dfrac{3}{4}\pi \right)$

Bấm vào đây để xem đáp án chi tiết

Ta có.

$y=4\sin \left( x+\dfrac{\pi }{6} \right)\cos \left( x-\dfrac{\pi }{6} \right)-\sin 2x=2\left( \sin 2x+\sin \dfrac{\pi }{3} \right)-\sin 2x=\sin 2x+\sqrt{3}$
Xét sự biến thiên của hàm số

$y=\sin 2x+\sqrt{3}$ , ta thấy với A, trên

$\left( 0;\dfrac{\pi }{4} \right)$ và

$\left( \dfrac{3\pi }{4};\pi \right)$ thì giá trị của hàm số tăng.

Câu 19: Hàm số $y=\sin x$ :

A
Đồng biến trên mỗi khoảng $\left( -\dfrac{3\pi } 2 +k2\pi ;\dfrac{5\pi } 2 +k2\pi \right)$ và nghịch biến trên mỗi khoảng $\left( -\dfrac{\pi } 2 +k2\pi ;\dfrac{\pi } 2 +k2\pi \right)$ với $k\in \mathbb Z$ .
B
Đồng biến trên mỗi khoảng $\left( \dfrac{\pi } 2 +k2\pi ;\pi +k2\pi \right)$ và nghịch biến trên mỗi khoảng $\left( \pi +k2\pi ;k2\pi \right)$ với $k\in \mathbb Z$ .
C
Đồng biến trên mỗi khoảng $\left( -\dfrac{\pi } 2 +k2\pi ;\dfrac{\pi } 2 +k2\pi \right)$ và nghịch biến trên mỗi khoảng $\left( \dfrac{\pi } 2 +k2\pi ;\dfrac{3\pi } 2 +k2\pi \right)$ với $k\in \mathbb Z$ .
D
Đồng biến trên mỗi khoảng $\left( \dfrac{\pi } 2 +k2\pi ;\dfrac{3\pi } 2 +k2\pi \right)$ và nghịch biến trên mỗi khoảng $\left( -\dfrac{\pi } 2 +k2\pi ;\dfrac{\pi } 2 +k2\pi \right)$ với $k\in \mathbb Z$ .

Bấm vào đây để xem đáp án chi tiết

Hàm số $y=\sin x$ đồng biến trên mỗi khoảng $\left( -\dfrac{\pi } 2 +k2\pi ;\dfrac{\pi } 2 +k2\pi \right)$ và nghịch biến trên mỗi khoảng $\left( \dfrac{\pi } 2 +k2\pi ;\dfrac{3\pi } 2 +k2\pi \right)$ với $k\in \mathbb Z$ .

Câu 20:
Trong khoảng $\left( 0;\dfrac{\pi }{2} \right)$ hàm số $y=\sin x-\cos x$ là hàm số

A
Không đổi.
B
Vừa đồng biến vừa nghịch biến.
C
Nghịch biến.
D
Đồng biến.

Bấm vào đây để xem đáp án chi tiết

Ta thấy trên khoảng

$\left( 0;\dfrac{\pi }{2} \right)$ hàm

$f\left( x \right)=\operatorname{sinx}$ đồng biến và hàm

$g\left( x \right)=-\cos x$ hàm

$y=-\cos x$ đồng biến

$\Rightarrow$ trên

$\left( 0;\dfrac{\pi }{2} \right)$ hàm số

$y=\sin x-\cos x$ đồng biến.

Xem thêm các bài tiếp theo bên dưới

Sự biến thiên hàm số lượng giác

Lý thuyết về Sự biến thiên hàm số lượng giác

Bài tập tự luyện có đáp án

Câu 1: Khẳng định nào sau đây đúng?

Câu 2: Hàm số y=cosx y=\cos x đồng biến trên đoạn nào dưới đây:

Câu 3: Trong các hàm số sau, hàm số nào đồng biến trên khoảng (−π3;π6)\left( -\dfrac{\pi }{3};\dfrac{\pi }{6} \right)

Câu 4: Cho hàm số y=sin2xy=\sin 2xđồng biến trên khoảng nào trong các khoảng sau?

Câu 5: Với x∈(0;π4)x\in \left( 0;\dfrac{\pi }{4} \right), mệnh đề nào sau đây đúng?

Câu 6: Hàm số y=sin2x y=\sin 2x nghịch biến trên khoảng nào sau đây (k∈Z) \left( k\in Z \right) .

Câu 7: Mệnh đề nào sau đây sai?

Câu 8: Cho hàm số y=sinxy=sinx. Mệnh đề nào sau đây là đúng?

Câu 9: Với x∈(31π4;33π4)x\in \left( \dfrac{31\pi }{4};\dfrac{33\pi }{4} \right), mệnh đề nào sau đây đúng?

Câu 10: Hàm số y=tanx y=\tan x đồng biến trên khoảng

Câu 13: Trong khoảng (π2+k2π;π+k2π),k∈Z \left( \dfrac{\pi }{2}+k2\pi ;\pi +k2\pi \right),k\in Z thì mệnh đề nào sau đây là sai?

Câu 14: Chọn khẳng định đúng?

Câu 15: Với k∈Z, k\in Z, kết luận nào sau đây về hàm số y=tan2x y=\tan 2x là sai?

Câu 16: Để hàm số y=sinx+cosx y=\sin x+\cos x tăng, ta chọn xx thuộc khoảng nào?

Câu 17: Hàm số y=cos2x y=\cos 2x nghịch biến trên khoảng nào sau đây (k∈Z) \left( k\in Z \right)

Câu 18: Cho hàm số y=4sin(x+π6)cos(x−π6)−sin2x y=4\sin \left( x+\dfrac{\pi }{6} \right)\cos \left( x-\dfrac{\pi }{6} \right)-\sin 2x . Kết luận nào sau đây là đúng về sự biến thiên của hàm số đã cho?

Câu 19: Hàm số y=sinx y=\sin x :

Câu 20: Trong khoảng (0;π2) \left( 0;\dfrac{\pi }{2} \right) hàm số y=sinx−cosx y=\sin x-\cos x là hàm số

Câu 2: Hàm số $y=\cos x$ đồng biến trên đoạn nào dưới đây:

Câu 3: Trong các hàm số sau, hàm số nào đồng biến trên khoảng $\left( -\dfrac{\pi }{3};\dfrac{\pi }{6} \right)$

Câu 4: Cho hàm số $y=\sin 2x$ đồng biến trên khoảng nào trong các khoảng sau?

Câu 5: Với $x\in \left( 0;\dfrac{\pi }{4} \right)$ , mệnh đề nào sau đây đúng?

Câu 6:
Hàm số $y=\sin 2x$ nghịch biến trên khoảng nào sau đây $\left( k\in Z \right)$ .

Câu 8: Cho hàm số $y=sinx$ . Mệnh đề nào sau đây là đúng?

Câu 9: Với $x\in \left( \dfrac{31\pi }{4};\dfrac{33\pi }{4} \right)$ , mệnh đề nào sau đây đúng?

Câu 10: Hàm số $y=\tan x$ đồng biến trên khoảng

Câu 13:
Trong khoảng $\left( \dfrac{\pi }{2}+k2\pi ;\pi +k2\pi \right),k\in Z$ thì mệnh đề nào sau đây là sai?

Câu 15:
Với $k\in Z,$ kết luận nào sau đây về hàm số $y=\tan 2x$ là sai?

Câu 16:
Để hàm số $y=\sin x+\cos x$ tăng, ta chọn $x$ thuộc khoảng nào?

Câu 17:
Hàm số $y=\cos 2x$ nghịch biến trên khoảng nào sau đây $\left( k\in Z \right)$

Câu 18:
Cho hàm số $y=4\sin \left( x+\dfrac{\pi }{6} \right)\cos \left( x-\dfrac{\pi }{6} \right)-\sin 2x$ . Kết luận nào sau đây là đúng về sự biến thiên của hàm số đã cho?

Câu 19: Hàm số $y=\sin x$ :

Câu 20:
Trong khoảng $\left( 0;\dfrac{\pi }{2} \right)$ hàm số $y=\sin x-\cos x$ là hàm số