Khối đa diện đều loại {p; q}
Lý thuyết về Khối đa diện đều loại {p; q}
+ Khái niệm: Một khối đa diện lồi được gọi là khối đa diện đều loại { p; q} nếu:
- Mỗi mặt của nó là một đa giác đều p cạnh.
- Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
+ Tính chất:
- Các mặt của khối đa diện đều là những đa giác đều và bằng nhau.
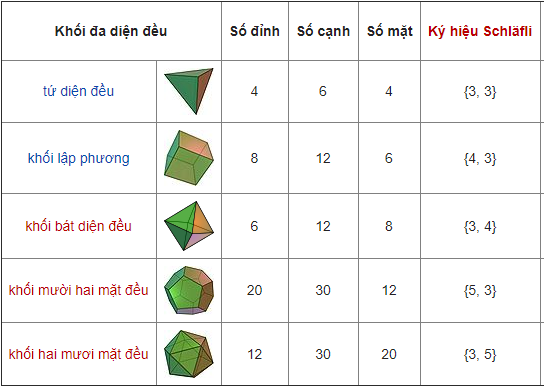
- Có năm loại khối đa diện đều. Đó là các khối đa diện đều loại {3; 3}, loại {4; 3}, loại {3; 4}, loại {5;3}, và loại {3;5}.
- Hai khối đa diện đều có cùng số mặt và có cạnh bằng nhau thì bằng nhau.
- Hai khối đa diện đều có cùng số mặt thì đồng dạng với nhau.
Bài tập tự luyện có đáp án
Câu 1: Trong các mệnh đề sau, mệnh đề nào đúng?
- A
- B
- C
- D
Ta có tứ diện có số đỉnh và số mặt bằng nhau
$\Rightarrow $ Tồn tại hình đa diện có số đỉnh và số mặt bằng nhau.
Câu 2: Số đỉnh của của khối đa diện có 20 mặt đều là
- A
- B
- C
- D
Hình 20 mặt đều có 12 đỉnh.
Câu 3: Số đỉnh của một bát diện đều là
- A
- B
- C
- D

Bát diện đều có $6$ đỉnh (hình minh họa).
Câu 4: Số cạnh của khối đa diện có $12$ mặt đều là
- A
- B
- C
- D
Câu 5: Hình đa diện nào dưới đây không có tâm đối xứng?


- A
- B
- C
- D
Câu 6: Có thể chia hình lập phương thành bao nhiêu hình hộp bằng nhau?
- A
- B
- C
- D
Câu 7: Cho hình hộp chữ nhật \(ABCD.A'B'C'D\). Các mệnh đề sau đây, mệnh đề nào SAI?
- A
- B
- C
- D

Do $A'BC\text{D}'$ hình chữ nhật nên $BD',A'C$ không vuông góc với nhau.
Vậy mệnh đề SAI là: ” Bốn đường chéo \(AC',BD',CA',DB'\) đôi một vuông góc”
Câu 8: Tâm tất cả các mặt của một hình lập phương là các đỉnh của hình
- A
- B
- C
- D
Câu 9: Số cạnh của một hình bát diện đều là
- A
- B
- C
- D
Hình bát diện đều có 12 cạnh.
Câu 10: Mệnh đề nào sau đây đúng?
- A
- B
- C
- D
Theo kiến thức SGK 12, có năm loại khối đa diện đều là $\left\{ 3;3 \right\},\left\{ 4;3 \right\},\left\{ 3;4 \right\},\left\{ 5;3 \right\},\left\{ 3;5 \right\}$.
Câu 11: Cho hình chóp tam giác đều $ S.ABC $ .Chọn khẳng định sai ?
- A
- B
- C
- D
Vì hình chóp tam giác đều có các mặt bên là các tam giác cân bằng nhau nên cạnh bên không bằng cạnh đáy.
Câu 12: Mỗi đỉnh của bát diện đều là đỉnh chung của
- A
- B
- C
- D
Mỗi đỉnh của bát diện đều là đỉnh chung của 4 cạnh.
Câu 13: Trong các mệnh đề sau, mệnh đề sai là:
- A
- B
- C
- D
Xem thêm các bài tiếp theo bên dưới