Đường kính và dây cung của đường tròn
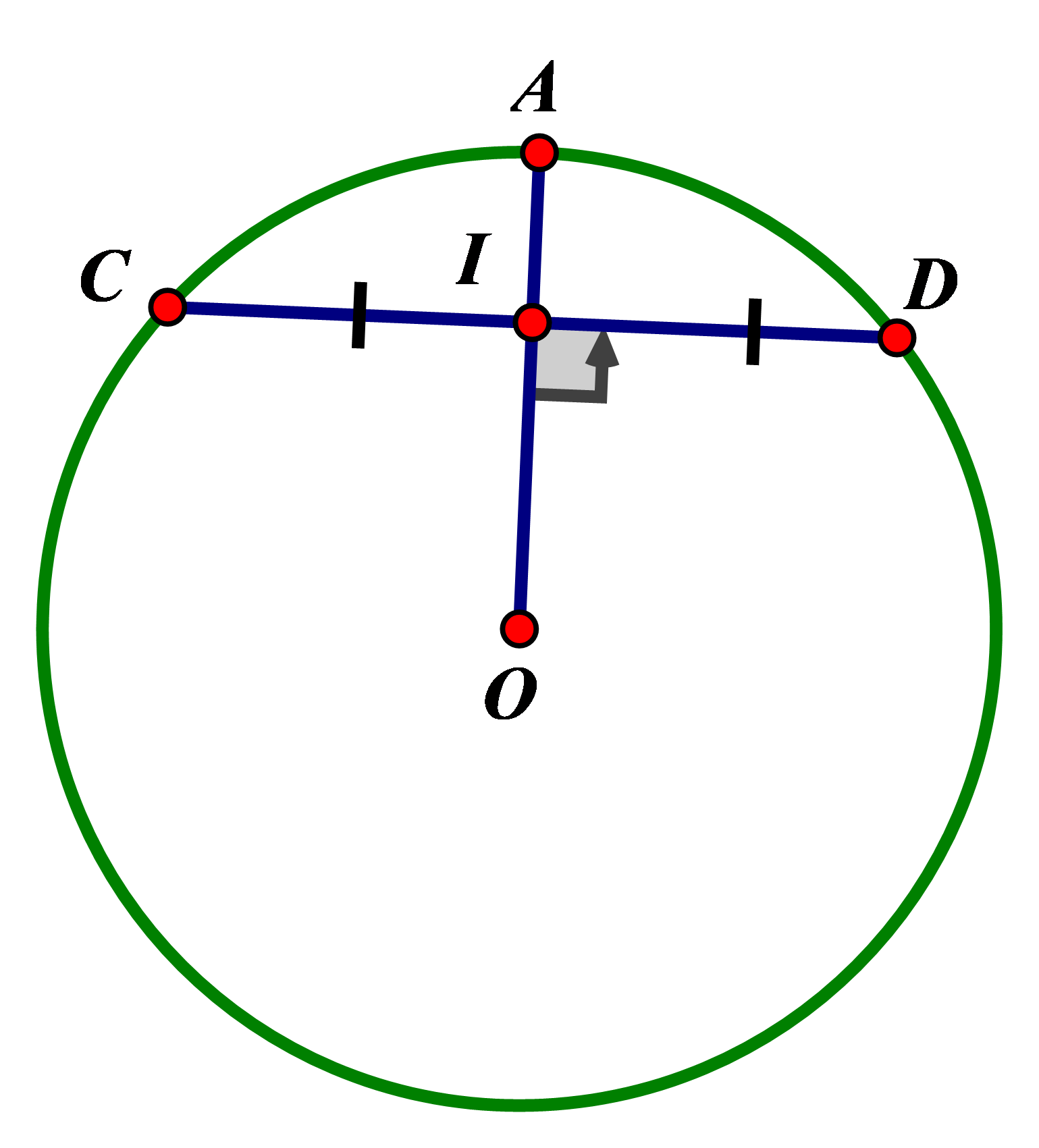
Lý thuyết về Đường kính và dây cung của đường tròn
1. So sánh độ dài của đường kính và dây
Trong các dây của một đường tròn, dây lớn nhất là đường kính
2. Quan hệ vuông góc giữa đường kính và dây
– Trong một đường tròn, đường kính vuông góc với một dây thì qua trung điểm của dây ấy.
– Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy
Bài tập tự luyện có đáp án
Câu 1: Cho đường tròn (O) có bán kính OA=3cm . Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính độ dài BC.
- A
- B
- C
- D

Gọi I là trung điểm của AB ⇒IO=IA=12OA=32cm
Ta có: BC⊥OA(gt)⇒ ^OIB=900
Áp dụng định lí Pi-ta-go vào tam giác vuông OIB ta có:
OB2=BI2+IO2 ⇒BI2=OB2−IO2⇒BI=3√32
Ta có: BI=CI (đường kính dây cung)
⇒BC=2BI=3√3(cm)
Câu 2: Cho đường tròn (O) đường kính AB và dây CD không đi qua tâm. Khẳng định nào sau đây là đúng?
- A
- B
- C
- D
Trong các dây của đường tròn, dây lớn nhất là đường kính.
Câu 3: "Trong một đường tròn, đường kính đi qua trung điểm một dây không đi qua tâm thì ... với dây ấy". điền vào dấu … cụm từ thích hợp.
- A
- B
- C
- D
Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
Câu 4: Cho đường tròn tâm (O) đường kính AB, CD không đi qua tâm. Khẳng định nào sau đây là đúng?
- A
- B
- C
- D
Do AB là đường kính nên AB là dây cung lớn nhất
Mặt khác CD không đi qua tâm nên CD<AB
Câu 5: Cho đường tròn tâm (O) hai dây AB, CD không đi qua tâm. Biết khoảng cách từ tâm O đến 2 dây bằng nhau. Khẳng định nào sau đây là đúng?
- A
- B
- C
- D
Do khoảng cách từ tâm O đến 2 dây bằng nhau nên CD=AB .
Câu 6: Chọn khẳng định sai trong các khẳng định sau. Trong hai dây của một đường tròn.
- A
- B
- C
- D
Trong một đường tròn:
+ Hai dây bằng nhau thì cách đều tâm.
Trong hai dây của một đường tròn:
+ Dây nào lớn hơn thì dây đó gần tâm hơn.
+ Dây nào gần tâm hơn thì dây đó lớn hơn.
Câu 7: Cho đường tròn (O), đường kính AD = 2R. Vẽ cung tâm D bán kính R, cung này cắt đường tròn (O) ở B và C. Số đo góc OAB bằng
- A
- B
- C
- D

Ta có DB=DC=DO=R
Mà OB=OC=R
Nên tam giác OBD là tam giác đều ⇒^BDA=600
Mà ^ABD=900⇒^BAD=900−600=300
Câu 8: "Trong các dây của một đường tròn, đường kính là dây có độ dài …". Cụm từ thích hợp điền vào chỗ trống là
- A
- B
- C
- D
Trong các dây của một đường tròn, đường kính là dây có độ dài lớn nhất.
Câu 9: Cho đường tròn (O) có bán kính R=5cm . Khoảng cách từ tâm đến dây AB là 3cm . Tính độ dài dây AB .
- A
- B
- C
- D
Kẻ OH⊥AB tại H suy ra H là trung điểm của AB .
Xét tam giác OHB vuông tại H có OH=3;OB=5 . Theo định lý Pytago ta có:
HB=√OB2−OH2=√52−32=4 .
Mà H là trung điểm của AB nên AB=2HB=8cm .
Vậy AB=8cm .
Câu 10: Cho đường tròn (O) có bán kính R=6,5cm . Khoảng cách từ tâm đến dây AB là 2,5cm . Tính độ dài dây AB .
- A
- B
- C
- D
Kẻ OH⊥AB tại H suy ra H là trung điểm của AB .
Xét tam giác OHB vuông tại H có OH=2,5;OB=6,5 . Theo định lý Pytago ta có HB=√OB2−OH2=√6,52−2,52=6 .
Mà H là trung điểm của AB nên AB=2HB=12cm .
Vậy AB=12cm .
Câu 11: "Trong một đường tròn, đường kính vuông góc với dây thì … của dây ấy". Điền vào dấu … cụm từ thích hợp.
- A
- B
- C
- D
Trong một đường tròn, đường kính vuông góc với dây thì đi qua trung điểm của dây ấy.
Câu 12: Trong đường tròn (O;2cm) , dây lớn nhất có độ dài bằng:
- A
- B
- C
- D
Dây lớn nhất trong đường tròn là đường kính d=2r=4cm .
Câu 13: Chọn khẳng định đúng trong các khẳng định sau. Trong hai dây của đường tròn.
- A
- B
- C
- D
Trong một đường tròn:
+ Hai dây bằng nhau thì cách đều tâm.
Trong hai dây của một đường tròn:
+ Dây nào lớn hơn thì dây đó gần tâm hơn.
+ Dây nào gần tâm hơn thì dây đó lớn hơn.
+ Hai dây đi qua tâm thì chưa chắc vuông góc với nhau.
Câu 14: Cho đường tròn (O) có hai dây AB,CD không đi qua tâm. Biết rằng khoảng cách từ tâm đến hai dây là bằng nhau. Kết luận nào sau đây là đúng?
- A
- B
- C
- D
Trong một đường tròn: Hai dây cách đều tâm thì bằng nhau.
Câu 15: Cho nửa đường tròn (O) , đường kính AB và một dây MN . Kẻ AE và BF vuông góc với MN lần lượt tại E và F . So sánh độ dài OE và OF .
- A
- B
- C
- D
Lấy I là trung điểm của EF .
Xét tứ giác AEFB có AE//FB (vì cùng vuông với EF ) nên AEFB là hình thang vuông tại E;F
Ta có OI là đường trung bình của hình thang AEFB nên OI//AE//FB⇒OI⊥EF
Hay OI⊥CD nên I là trung điểm của CD (quan hệ giữa dây và đường kính)
Xét tam giác OEF có OI vừa là đường cao vừa là đường trung tuyến nên ΔOEF cân tại O . Suy ra OE=OF .
Câu 16: Cho đường tròn (O) có hai dây AB,CD không đi qua tâm. Biết rằng khoảng cách từ tâm đến dây AB lớn hơn khoảng cách từ tâm O đến dây CD . Kết luận nào sau đây là đúng?
- A
- B
- C
- D
Trong một đường tròn: Dây nào gần tâm hơn thì dây đó lớn hơn.
Từ đề bài ta thấy dây CD gần tâm hơn dây AB nên CD>AB .
Xem thêm các bài tiếp theo bên dưới