Đồ thị hàm trùng phương
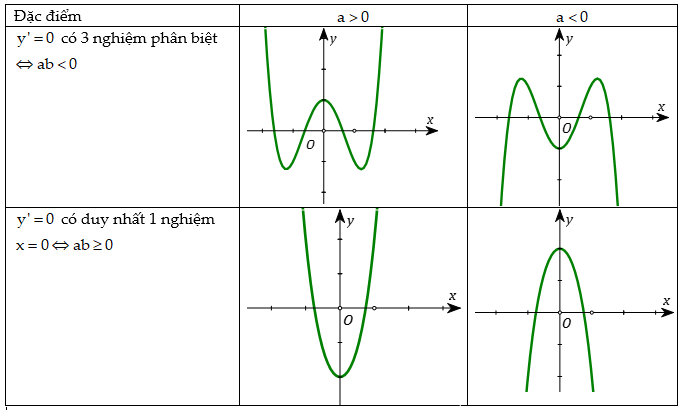
Lý thuyết về Đồ thị hàm trùng phương
Dạng hàm; $y=ax^4+bx^2+c,a\ne 0$
Hệ số c là tung độ giao điểm đồ thị với $Oy$
Đồ thị là hàm chẵn chỉ có trục đối xứng không có tâm đối xứng
Bài tập tự luyện có đáp án
Câu 1: Đồ thị hàm số nào sau đây luôn nằm phía trên trục hoành
- A
- B
- C
- D
Bằng máy tính dễ dàng kiểm tra được phương trình ${{x}^{4}}+2{{x}^{2}}+1=0$ vô nghiệm. Hay đồ thị hàm số không cắt trục $Ox$, mà hệ số của ${{x}^{4}}$ là $1>0$ từ đây từ hình dạng đồ thị hàm bậc $4$ ta suy ra đáp án cần tìm là $y={{x}^{4}}+2{{x}^{2}}+1$.
Câu 2: Số giao điểm của đồ thị của hàm số $y=a{{x}^{4}}+b{{\text{x}}^{2}}+c\left( a\ne 0 \right)$ và trục $Oy$ là
- A
- B
- C
- D
Dựa vào dạng đồ thị của hàm số $y=a{{x}^{4}}+b{{\text{x}}^{2}}+c\left( a\ne 0 \right)$ trong SGK CB trang 38, ta có số giao điểm của đồ thị và trục $Oy$ là $1$.
Câu 3: Cho hàm số $y={{x}^{4}}+b{{x}^{2}}+c$. Đồ thị hàm số và tiếp tuyến tại điểm cực trị cắt nhau nhiều nhất tại mấy điểm?
- A
- B
- C
- D
Đồ thị hàm số và tiếp tuyến tại điểm cực trị cắt nhau nhiều nhất tại $3$ điểm được thể hiện như hình vẽ.

Câu 4: Hàm số nào dưới đây có đồ thị như trong hình bên?


- A
- B
- C
- D
Đây là đồ thị hàm số $ y=a{{x}^{4}}+b{{x}^{2}}+c\left( a\ne 0 \right) $ có $ a > 0 $ .
Câu 5:  Đường cong trong hình vẽ bên là đồ thị của một trong bốn hàm số sau. Hỏi đó là đồ thị của hàm số nào?
Đường cong trong hình vẽ bên là đồ thị của một trong bốn hàm số sau. Hỏi đó là đồ thị của hàm số nào?
 Đường cong trong hình vẽ bên là đồ thị của một trong bốn hàm số sau. Hỏi đó là đồ thị của hàm số nào?
Đường cong trong hình vẽ bên là đồ thị của một trong bốn hàm số sau. Hỏi đó là đồ thị của hàm số nào?- A
- B
- C
- D
Ta thấy đồ thị cắt Oy tại điểm (0;2) và cắt Ox tại điểm (2;0) => hàm số $ y=\dfrac{x-2}{x-1}$ thỏa mãn.
Câu 6:  Đồ thị hình vẽ bên là đồ thị của một trong 4 hàm số được liệt kê ở các phương án dưới đây. Hỏi đó là hàm số nào?
Đồ thị hình vẽ bên là đồ thị của một trong 4 hàm số được liệt kê ở các phương án dưới đây. Hỏi đó là hàm số nào?
 Đồ thị hình vẽ bên là đồ thị của một trong 4 hàm số được liệt kê ở các phương án dưới đây. Hỏi đó là hàm số nào?
Đồ thị hình vẽ bên là đồ thị của một trong 4 hàm số được liệt kê ở các phương án dưới đây. Hỏi đó là hàm số nào?- A
- B
- C
- D
Đồ thị hàm số có tiệm cận đứng là $ x=-2 $ và tiệm cận ngang là $ y=-2 $ $ \Rightarrow $ loại 2 phương án $ y=\dfrac{2x-1}{x-2} $ và $ y=\dfrac{2x-1}{x+2} $
Lại có đồ thị hàm số cắt trục Ox tại điểm có hoành độ dương $ \Rightarrow $ chọn đáp án $ y=\dfrac{-2x+1}{x+2} $ .
Câu 7: Cho hàm số đồ thị dạng như hình bên.
 Khẳng định nào sau đâu là khẳng định đúng ?
Khẳng định nào sau đâu là khẳng định đúng ?
 Khẳng định nào sau đâu là khẳng định đúng ?
Khẳng định nào sau đâu là khẳng định đúng ?- A
- B
- C
- D
Hình bên là đồ thị của hàm bậc 4 trùng phương hoặc đồ thị hàm số bậc 2.
Nhận thấy đồ thị không đối xứng qua Ox nên là dạng đồ thị của hàm số bậc 2.
Câu 8: Bảng biến thiên ở bên là của hàm số nào?


- A
- B
- C
- D
Đồ thị hàm số hướng lên $ \Rightarrow $ loại $ y=-{ x ^ 4 }+3{ x ^ 2 }+1 $ và $ y=-{ x ^ 4 }-3{ x ^ 2 }+1 $
Hàm số đi qua điểm $ \left( 0;-1 \right) $ $ \Rightarrow $ chọn đáp án $ y={ x ^ 4 }+3{ x ^ 2 }-1 $
Câu 9: Hình bên là đồ thị của hàm số


- A
- B
- C
- D
Vì đồ thị hàm số đi qua điểm $\left( 3;0 \right)$ nên loại $y=\dfrac{x+3}{x-1}$và $y=\dfrac{x-1}{x-3}$
Từ đồ thị ta thấy hàm số luôn đồng biến trên các khoảng của TXĐ nên loại $y=\dfrac{3-x}{x-1}$
Câu 10: Cho bảng biến thiên của hàm số \[y=f\left( x \right)\] như hình vẽ
 Khẳng định nào sau đây là khẳng đinh sai?
Khẳng định nào sau đây là khẳng đinh sai?
 Khẳng định nào sau đây là khẳng đinh sai?
Khẳng định nào sau đây là khẳng đinh sai?- A
- B
- C
- D
Từ BBT ta thấy hàm số đồng biến trên \[\left( 2;+\infty \right)\].
Vậy khẳng định “Hàm số đồng biến trên \[\left( 0;2 \right)\]” sai.
Câu 11:  Đường cong ở hình là đồ thị của hàm số nào trong bốn hàm số ở dưới đây?
Đường cong ở hình là đồ thị của hàm số nào trong bốn hàm số ở dưới đây?
 Đường cong ở hình là đồ thị của hàm số nào trong bốn hàm số ở dưới đây?
Đường cong ở hình là đồ thị của hàm số nào trong bốn hàm số ở dưới đây?
- A
- B
- C
- D
Đây là đồ thị hàm số có dạng $y=a{{x}^{3}}+b{{x}^{2}}+cx+d$ hơn nữa ta thấy khi $x\to +\infty $ thì $y\to +\infty $ do đó $a>0$.
Câu 12: Đồ thị sau là của hàm số nào?


- A
- B
- C
- D
Đồ thị TCĐ $ x=1 $ , TCN $ y=1 $ $ \Rightarrow $ loại phương án $ y=\dfrac{x-1}{x+1} $ và $ y=\dfrac{-x}{1-x} $
Đồ thị đi qua điểm $ x=0,y=-1 $ $ \Rightarrow $ chọn đáp án $ y=\dfrac{x+1}{x-1} $ .
Câu 13: Bảng biến thiên ở bên là của hàm số nào?


- A
- B
- C
- D
Từ trái sang phải đồ thị hàm số đi lên $ \Rightarrow $ hệ số của $ { x ^ 3 } $ lớn hơn 0 $ \Rightarrow $ loại 2 phương án $ y=-{ x ^ 3 }+3{ x ^ 2 }-3x $ và $ y=-{ x ^ 3 }-3{ x ^ 2 }-3x $
Phương trình $ y'=0 $ có nghiệm $ x=1 $ $ \Rightarrow $ chọn đáp án $ y={ x ^ 3 }-3{ x ^ 2 }+3x $
Câu 14: Hàm số nào sau đây không có tâm đối xứng ?
- A
- B
- C
- D
Hàm bậc 4 trùng phương đối xứng qua trục Oy và không có tâm đối xứng.
Câu 15: Cho hàm số $y=a{{x}^{4}}-2{{x}^{2}}+c\left( a\ne 0 \right)$ có đồ thị như hình vẽ bên . Khẳng định đúng là:


- A
- B
- C
- D
Đây là đồ thị hàm trùng phương có hệ số $a>0$ , đồ thị cắt trục $Oy$ tại điểm có tung độ âm suy ra $c<0$
Câu 16: Đồ thị hình bên là của hàm số nào?


- A
- B
- C
- D
Từ đồ thị ta thấy, đây là đồ thị hàm trùng phương $ y=a{ x ^ 4 }+b{ x ^ 2 }+c $
Từ dáng đồ thị $ \Rightarrow a > 0 $ $ \Rightarrow $ loại phương án $ y=-\dfrac{1}{4} { x ^ 4 }+3{ x ^ 2 }-1 $ .
Mà từ đồ thị ta thấy, hàm số chỉ có 1 cực trị tại $ x=0 $ $ \Rightarrow $ chọn $ y={ x ^ 4 }+2{ x ^ 2 }-1 $.
Câu 17: Điểm đối xứng của đồ thị hàm số cho trong hình bên là:


- A
- B
- C
- D
Hàm bậc nhất trên bậc nhất nhận giao điểm của hai đường tiệm cân làm tâm đối xứng,đồ thị hàm số trên có hai đường tiệm cận \(x=1,y=2\) nên có tâm đối xứng là \(\left( 1;2 \right)\).
Câu 18: Cho hàm số $ y=f\left( x \right) $ có đồ thị là đường cong trong hình vẽ bên. Hàm số $ y=f\left( x \right) $ đạt cực đại tại điểm nào sau đây?


- A
- B
- C
- D
Nhìn vào đồ thị ta thấy hàm số đạt cực đại tại $ x=-1 $
Câu 19: Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số cho dưới đây:


- A
- B
- C
- D
Đồ thị có hình dạng là đường bậc 2 hoặc bậc 4 trùng phương, nên loại $y=-{{x}^{3}}+3x+2$
Đồ thị có cực đại là $\left( 0;2 \right)$ nên $f\left( 0 \right)=2$, vậy chọn $y=-\dfrac{{{x}^{4}}}{2}-{{x}^{2}}+2$
Câu 20: Bảng biến thiên sau là của hàm số nào?


- A
- B
- C
- D
\[\begin{array}{l}
y = a{x^4} + b{x^2} + c\\
\left\{ \begin{array}{l}
y\left( 0 \right) = - 3\\
y\left( 1 \right) = - 4\\
y'\left( 1 \right) = 0
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
a = 1\\
b = - 2\\
c = - 3
\end{array} \right. \Rightarrow y = {x^4} - 2{x^2} - 3
\end{array}\]
Câu 21: Đồ thị hình bên là của hàm số nào?


- A
- B
- C
- D
Từ đồ thị ta thấy, đây là đồ thị hàm trùng phương $ y=a{ x ^ 4 }+b{ x ^ 2 }+c $
Từ dáng đồ thị $ \Rightarrow a > 0 $ $ \Rightarrow $ loại phương án $ y=-{ x ^ 4 }+4{ x ^ 2 }-1 $ .
Mà từ đồ thị ta thấy, hàm số đạt cực trị tại $ x=\pm 1 $ $ \Rightarrow $ loại phương án $ y={ x ^ 4 }-4{ x ^ 2 }-1 $
Đồ thị hàm số đi qua điểm $ \left( 0;-1 \right)\Rightarrow $ chọn đáp án là $ y={ x ^ 4 }-2{ x ^ 2 }-1 $ .
Câu 22: Đồ thị sau là của hàm số nào?


- A
- B
- C
- D
\[y = a{x^4} + b{x^2} + c\]. Từ đồ thị suy ra $a<0$.
Đồ thị hàm số đi qua điểm $(0,0)$, suy ra $c=0$.
Đồ thị hàm số đi qua điểm \[\left( {\sqrt 2 ;4} \right)\] suy ra chọn D.
Câu 23: Đồ thị của hàm số nào dưới đây có dạng như đường cong hình vẽ bên


- A
- B
- C
- D
Đồ thị hàm số có hai điểm cực trị nên loại $ y={{x}^{4}}-2{{x}^{2}}+3 $ và $ y=-{{x}^{4}}+2{{x}^{2}}+3 $
Khi $ x\to -\infty $ thì $ y\to -\infty $ nên hệ số $ a > 0 $ .
Vậy chọn $ y={{x}^{3}}-3{{x}^{2}}+3 $
Câu 24:  Cho hàm số $ y=f\left( x \right) $ có đồ thị như hình vẽ kề bên. Khẳng định nào sau đây là sai?
Cho hàm số $ y=f\left( x \right) $ có đồ thị như hình vẽ kề bên. Khẳng định nào sau đây là sai?
 Cho hàm số $ y=f\left( x \right) $ có đồ thị như hình vẽ kề bên. Khẳng định nào sau đây là sai?
Cho hàm số $ y=f\left( x \right) $ có đồ thị như hình vẽ kề bên. Khẳng định nào sau đây là sai?- A
- B
- C
- D
Câu 25: Cho hàm số $y=ax^4+bx^2+c\left( a\ne 0 \right)$. Trong các khẳng định, khẳng định sai là
- A
- B
- C
- D
Vì $y\left( -x \right)=a{{\left( -x \right)}^{4}}+b{{\left( -x \right)}^{2}}+c=a{{x}^{4}}+b{{\text{x}}^{2}}+c=y\left( x \right)$
$\Rightarrow $ Hàm số là hàm số chẵn.
Vậy khẳng định “Hàm số là hàm số lẻ” là sai.
Câu 26: Bảng biến thiên ở bên là của hàm số nào?


- A
- B
- C
- D
Đồ thị hàm số hướng lên $ \Rightarrow $ loại $ y=-{ x ^ 4 }-3{ x ^ 2 }-3 $
Hàm số đi qua điểm $ \left( 1;-4 \right) $ $ \Rightarrow $ chọn đáp án $ y={ x ^ 4 }-2{ x ^ 2 }-3 $
Câu 27: Hàm số $y=f\left( x \right)$ xác định trên $\mathbb{R}$, có bảng biến thiên trên đoạn $\left[ -3;2 \right]$ sau:
 Khẳng định nào sau đây là sai ?
Khẳng định nào sau đây là sai ?
 Khẳng định nào sau đây là sai ?
Khẳng định nào sau đây là sai ?- A
- B
- C
- D
Vì bảng biến thiên này chỉ xét trên đoạn $\left[ -3;2 \right]$ chứ không phải trên R, nên ta không thể kết luận được số cực trị của hàm số được. Do đó khẳng định : "Hàm số có 2 cực trị." là sai
Câu 28:  Cho hàm số $ y=f\left( x \right) $ có đồ thị như hình vẽ bên.
Mệnh đề nào sau đây đúng về hàm số đó?
Cho hàm số $ y=f\left( x \right) $ có đồ thị như hình vẽ bên.
Mệnh đề nào sau đây đúng về hàm số đó?
 Cho hàm số $ y=f\left( x \right) $ có đồ thị như hình vẽ bên.
Mệnh đề nào sau đây đúng về hàm số đó?
Cho hàm số $ y=f\left( x \right) $ có đồ thị như hình vẽ bên.
Mệnh đề nào sau đây đúng về hàm số đó?- A
- B
- C
- D
Phương pháp:
+) Dựa vào đồ thị hàm số nhận xét những đặc điểm của đồ thì và chọn kết luận đúng.
Cách giải:
Dựa vào đồ thị hàm số suy ra đồ thị hàm số đồng biến trên $ \left( -1;0 \right)\text{ }v\grave{a}\text{ }\left( 2;+\infty \right), $ nghịch biến trên $ \left( -\infty ;-1 \right) $ và $ \left( 0;2 \right) $
Câu 29: Hình bên là đồ thị của hàm số


- A
- B
- C
- D
Dựa vào SGK ta biết được hình dạng quen thuộc của đồ thị các hàm số $y=\dfrac{x-1}{x+1}$, $y={{x}^{4}}-{{x}^{2}}$, $y=\dfrac{1}{2}{{x}^{3}}+{{x}^{2}}-3$.
$\Rightarrow $ Hình bên là đồ thị của hàm số $y={{x}^{4}}-2{{\text{x}}^{3}}$.
Câu 30:  Hình bên là đồ thị của hàm số nào dưới đây
Hình bên là đồ thị của hàm số nào dưới đây
 Hình bên là đồ thị của hàm số nào dưới đây
Hình bên là đồ thị của hàm số nào dưới đây- A
- B
- C
- D
Đây là đồ thị hàm bậc $4$ và đi qua điểm $A\left( 0;2 \right)$ nên chỉ có đáp án $y=-{{x}^{4}}+2{{x}^{2}}+2$ là thỏa mãn.
Câu 31: Hình vẽ dưới đây là đồ thị của hàm số nào ?


- A
- B
- C
- D
Từ đồ thị ta thấy đây là đồ thị của hàm bậc 3 $ y=a{ x ^ 3 }+b{ x ^ 2 }+cx+d $ $ \Rightarrow $ loại phương án $ y=\dfrac{2x-2}{x+1} $ và $ y={ x ^ 4 }+{ x ^ 2 }-2 $
Từ trái sang phải, đồ thị hàm số đi lên $ \Rightarrow a > 0 $ . Đồ thị hàm số đi qua điểm $ \left( 0;-2 \right) $ $ \Rightarrow $ chọn đáp án là $ y={ x ^ 3 }+x-2 $
Câu 32: Đồ thị hình bên là của hàm số nào?

Đồ thị hình bên là của hàm số nào?

- A
- B
- C
- D
Đồ thị TCĐ $x=-1$ nên loại $y=\dfrac{-2x+1}{2x+1}$
Đồ thị hàm số đi qua điểm có tọa độ $\left( 0;1 \right)$ nên loại $y=\dfrac{-x}{x+1}$ và $y=\dfrac{-x+2}{x+1}$
Câu 33: Cho bảng biến thiên của hàm số $y=f\left( x \right)$ như hình bên.
Khẳng định nào sau đây là sai?

Khẳng định nào sau đây là sai?

- A
- B
- C
- D
Từ BBT ta thấy $\underset{x\to -\infty }{\mathop{\lim }}\,y=-2\Rightarrow y=-2$ là tiệm cận ngang.
Mặt khác $\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,y=+\infty \Rightarrow x=0$ làm tiệm cận đứng và $\underset{x\to 2}{\mathop{\lim }}\,y=0\Rightarrow x=2$ không là tiệm cận đứng.
Vậy khẳng định “Đồ thị hàm số nhận $x=2$ làm tiệm cận đứng” sai.