Định nghĩa đường tròn, tính chất của đường tròn
Lý thuyết về Định nghĩa đường tròn, tính chất của đường tròn
1. Định nghĩa đường tròn
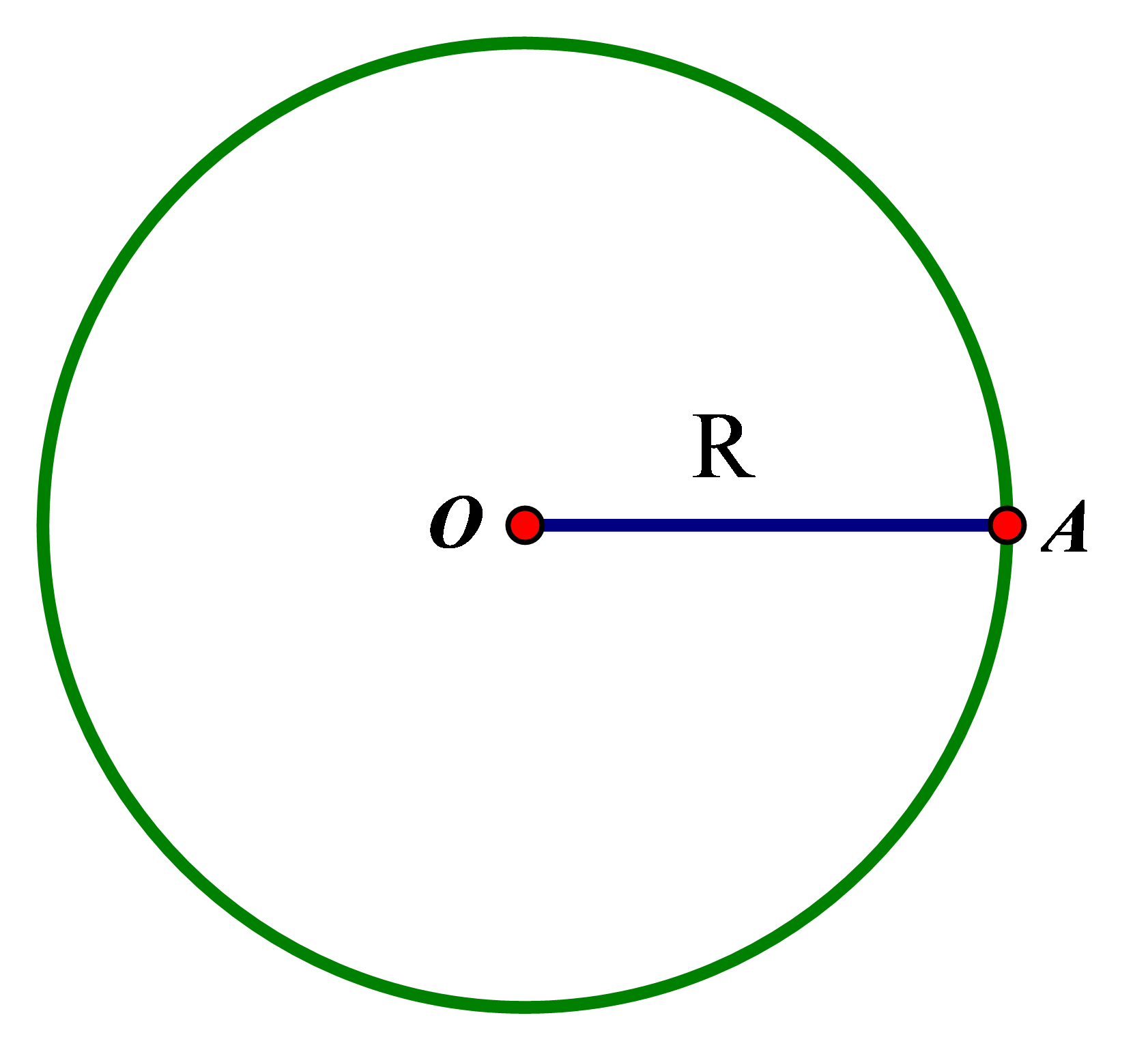
Đường tròn tâm OO bán kính RR, kí hiệu (O;R)(O;R), là hình gồm các điểm cách OO một khoảng bằng R.R.
Nếu AA nằm trên đường tròn (O;R)(O;R) thì OA=ROA=R
Nếu AA nằm trong đường tròn (O;R)(O;R) thì OA<ROA<R
Nếu AA nằm ngoài đường tròn (O;R)(O;R) thì OA>R.OA>R.
2. Định lí về sự xác định một đường tròn
Qua ba điểm không thẳng hàng, ta vẽ được một và chỉ một đường tròn.
Tâm OO của đường tròn đi qua ba điểm A,B,CA,B,C là giao điểm của ba đường trung trực của tam giác ABC.ABC.
3. Tính chất đối xứng của đường tròn
Đường tròn là hình có tâm đối xứng và có trục đối xứng: tâm đối xứng là tâm đường tròn, trục đối xứng là bất kỳ đường kính nào.
Bài tập tự luyện có đáp án
Câu 1: Cho hình thoi ABCDABCD có cạnh bằng 10cm10cm và ˆA=600ˆA=600 . Gọi O là giao điểm của hai đường chéo; E, F, G, H theo thứ tự là trung điểm của AB,BC,CD,DAAB,BC,CD,DA . Biết sáu điểm E,B,F,G,D,HE,B,F,G,D,H thuộc cùng một đường tròn. Bán kính của đường tròn đó là
- A
- B
- C
- D
Do ˆA=600⇒ΔABD;ΔCBDˆA=600⇒ΔABD;ΔCBD là 2 tam giác đều ⇒OB=OD=5cm⇒OB=OD=5cm
Ta có OE;OHOE;OH là 2 đường trung bình trong tam giác ABDABD nên OE=OH=AB2=5cmOE=OH=AB2=5cm
Ta có OF;OGOF;OG là 2 đường trung bình trong tam giác CBDCBD nên OF=OG=BC2=5cmOF=OG=BC2=5cm
Vậy sáu điểm E,B,F,G,D,HE,B,F,G,D,H thuộc cùng một đường tròn tâm O bán kính R=5cmR=5cm
Câu 2: Cho hình vuông ABCDABCD , có cạnh bằng 8cm8cm . Khi đó bán kính đường tròn qua 4 đỉnh của hình vuông là
- A
- B
- C
- D
Gọi I là giao điểm của hai đường chéo AC và BD.
Ta có: IA=IB=IC=IDIA=IB=IC=ID (tính chất của hình vuông)
Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn. Tâm của đường tròn là I.
Áp dụng định lí Pitago vào tam giác vuông ABC ta có:
AC2=AB2+BC2=82+82=2.64⇒AC=8√2cm⇒IA=AC2=4√2cm
Câu 3: Cho tam giác ABC vuông tại A , có AB=15cm;AC=20cm . Tính bán kính đường tròn ngoại tiếp tam giác ABC .
- A
- B
- C
- D
Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp là trung điểm cạnh huyền BC , bán kính là R=BC2 .
Theo định lý Pytago ta có BC=√AC2+AB2=25 nên bán kính R=252 .
Câu 4: Cho tam giác nhọn ABC. Vẽ đường tròn (O) có đường kính BC, nó cắt các cạnh AB, AC theo thứ tự ở D, E. Gọi K là giao điểm của BE và CD. Khi đó điểm K là
- A
- B
- C
- D
Ta có
D∈(O;BC2)⇒^BDC=900E∈(O;BC2)⇒^BEC=900
Khi đó K là trực tâm tam giác ABC
Câu 5: Cho tam giác ABC nội tiếp đường tròn (O). Khi đó số khẳng định đúng, trong các khẳng định sau là
I) Nếu BC là đường kính của đường tròn thì ^BAC=900
II) Nếu AB=AC thì AO vuông góc với BC.
III) Nếu tam giác ABC không vuông thì điểm O nằm bên trong tam giác đó.
Khi đó số khẳng định đúng, trong các khẳng định sau là
I) Nếu BC là đường kính của đường tròn thì ^BAC=900
II) Nếu AB=AC thì AO vuông góc với BC.
III) Nếu tam giác ABC không vuông thì điểm O nằm bên trong tam giác đó.
- A
- B
- C
- D
Khẳng định (I) đúng
Ta có O thuộc đường trung trực của BC nên nếu AB=AC thì đường trung trực của BC sẽ qua A ⇒OA⊥BC
Khẳng định (III) là sai. Do tam giác ABC nếu có 1 góc tù thì O nằm ngoài tam giác ABC
Câu 6: Cho tam giác ABC có các đường cao BD,CE . Biết rằng bốn điểm B,E,D,C cùng nằm trên một đường tròn. Chỉ rõ tâm và bán kính của đường tròn đó.
- A
- B
- C
- D
Gọi I là trung điểm của BC .
Xét tam giác BEC vuông tại E có EI=IB=IC=BC2 (vì EI là đường trung tuyến ứng với cạnh huyền).
Xét tam giác BDC vuông tại D có DI=IB=IC=BC2 (vì DI là đường trung tuyến ứng với cạnh huyền).
Từ đó ta có ID=IE=IB=IC=BC2 nên I là tâm đường tròn ngoại tiếp tứ giác DEBC và bán kính R=BC2 .
Câu 7: Trong các câu sau, có bao nhiêu khẳng định sai? I. Hai đường tròn phân biệt có thể có hai điểm chung
II. Hai đường tròn phân biệt có thể có ba điểm chung phân biệt
III.Tâm của đường tròn ngoại tiếp một tam giác bao giờ cũng nằm trong tam giác ấy.
I. Hai đường tròn phân biệt có thể có hai điểm chung
II. Hai đường tròn phân biệt có thể có ba điểm chung phân biệt
III.Tâm của đường tròn ngoại tiếp một tam giác bao giờ cũng nằm trong tam giác ấy.
- A
- B
- C
- D
I. Đúng
II. Sai vì hai đường tròn có ba điểm chung phân biệt thì chúng trùng nhau
III. Sai vì tam giác vuông có tâm đường tròn ngoại tiếp nằm trên cạnh huyền, tam giác tù giao điểm của ba đường trung trực nằm ngoài tam giác.
Câu 8: Cho hình chữ nhật ABCD có AB=8cm,BC=6cm . Tính bán kính đường tròn đi qua bốn đỉnh A,B,C,D .
- A
- B
- C
- D
Gọi I là giao hai đường chéo, ta có IA=IB=IC=ID (vì BD=AC và I là trung điểm mỗi đường)
Nên bốn điểm A,B,C,D cùng thuộc đường tròn tâm I bán kính R=AC2
Theo định lý Pytago trong tam giác vuông ABC ta có AC=√AB2+BC2=√82+62=10 nên R=AC2=102=5cm .
Vậy bán kính cần tìm là R=5cm .
Câu 9: Cho hình chữ nhật ABCD có AD=8cm,CD=6cm . Biết rằng bốn điểm A, B, C, D cùng thuộc một đường tròn. Bán kính của đường tròn đó bằng
- A
- B
- C
- D
Gọi I là giao điểm của hai đường chéo AC và BD. Ta có:
IA=IB=IC=ID (tính chất hình chữ nhật)
Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn bán kính AC2
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC ta có:
AC2=AB2+BC2=42+32=52⇒AC=5⇒IA=52
Câu 10: Chọn khẳng định SAI trong các khẳng định sau:
- A
- B
- C
- D
Vì qua ba điểm không thẳng hàng xác định được duy nhất một đường tròn. Nên khẳng định qua ba điểm không thẳng hàng, xác định được vô số đường tròn là khẳng định SAI.
Câu 11: Xác định tâm và bán kính của đường tròn đi qua cả bốn đỉnh của hình vuông ABCD cạnh a .
- A
- B
- C
- D
Gọi O là giao hai đường chéo của hình vuông ABCD . Khi đó theo tính chất của hình vuông ta có OA=OB=OC=OD nên O là tâm đường tròn ngoại tiếp hình vuông ABCD , bán kính R=OA=AC2 .
Xét tam giác ABC vuông cân tại B ta có AC2=AB2+BC2⇒AC=a√2⇒R=a√22
Vậy tâm đường tròn ngoại tiếp hình vuông ABCD cạnh a là giao điểm hai đường chéo, bán kính là R=a√22 .
Câu 12: Cho hình vuông ABCD . Gọi M,N lần lượt là trung điểm của AB,BC . Gọi E là giao điểm của CM và DN . Tâm của đường tròn đi qua bốn điểm A,D,E,M là
- A
- B
- C
- D
+ Ta có ΔDCN=ΔCMB (c – g – c)
⇒^CDN=^ECN nên ^CNE+^ECN=^CNE+^CDN=90∘ suy ra ^CEN=90∘⇒CM⊥DN
+ Gọi I là trung điểm của DM .
Xét tam giác vuông ADM ta có AI=ID=IM=DM2 .
Xét tam giác vuông DEM ta có EI=ID=IM=DM2 .
Nên EI=ID=IM=IA=DM2 .
Do đó bốn điểm A,D,E,M cùng thuộc đường tròn tâm I bán kính DM2 .
Câu 13: Cho tam giác đều ABC cạnh bằng 3cm . Bán kính của đường tròn ngoại tiếp tam giác ABC bằng
- A
- B
- C
- D
Vì O là tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm của ba đường trung trực trong tam giác ABC.
Kẻ AH⊥BC . Ta có: O∈AH
Trong tam giác vuông ABH , ta có: AH=AB.sinˆC=3.sin600=3√32
Vì tam giác ABC đều nên AH là đường cao cũng đồng thời là trung tuyến nên:
OA=23AH=23⋅3√32=√3
Câu 14: Trên mặt phẳng tọa độ Oxy , cho 2 điểm A(−2;3);B(2;√5) và đường tròn (O;3) . Khi đó ta có
- A
- B
- C
- D
Ta có OA=√(−2)2+(−3)2=√13>R=3 ; khi đó điểm A nằm bên ngoài đường tròn.
Ta có OB=√(2)2+(−√5)2=3=R ; khi đó điểm B nằm bên trên đường tròn.
Câu 15: Cho tam giác đều ABC cạnh bằng a , các đường cao là BM và CN . Gọi O là trung điểm cạnh BC . Đường tròn đi qua bốn điểm B,N,M,C là
- A
- B
- C
- D

D là trung điểm BC
Xét hai tam giác vuông BNC và BMC có ND,MD là hai đường trung tuyến.
⇒DN=DB=DC=DM=BC2 nên bốn điểm B,N,M,C cùng thuộc đường tròn tâm D bán kính BC2 .
Câu 16: Cho tam giác ABC cân tại A , đường cao AH=4cm,BC=6cm . Đường vuông góc với AC tại C cắt đường thẳng AH ở D . Tính đường kính của đường tròn đi qua các điểm A,B,D,C .
- A
- B
- C
- D
Từ câu trước ta có bốn điểm A,B,D,C cùng thuộc đường tròn đường kính AD suy ra ta cần tính độ dài AD .
Vì BC=6cm⇒BH=3cm . Áp dụng định lý Pytago cho tam giác vuông AHB ta được AB=√AH2+BH2=√42+32=5 .
Áp dụng hệ thức lượng trong tam giác vuông ABD ta có AB2=AH.AD⇒AD=AB2AH=524=6,25 .
Vậy đường kính cần tìm là 6,25cm .
Câu 17: Có bao nhiêu đường tròn đi qua 2 điểm phân biệt:
- A
- B
- C
- D
Vì tâm chúng nằm trên trung trực của của đoạn thẳng nối 2 điểm đó.
Câu 18: Cho tam giác ABC cân tại A , đường cao AH=4cm,BC=6cm . Đường vuông góc với AC tại C cắt đường thẳng AH ở D . Chọn câu sai.
- A
- B
- C
- D
Ta có ΔABC cân tại A có đường cao AH nên AH cũng là đường phân giác ⇒^CAD=^DAB .
Suy ra ΔACD=ΔABD (c – g – c) nên ^ABD=^ACD=90∘ và CD=DB .
Lấy I là trung điểm AD .
Xét hai tam giác vuông ABD và ACD có IA=ID=IB=IC=AD2 .
Nên I là điểm cách đều A,B,D,C hay A,B,D,C cùng nằm trên đường tròn tâm I đường kính AD .
Câu 19: Cho tam giác đều ABC cạnh bằng a , các đường cao là BM và CN . Gọi D là trung điểm cạnh BC . Bốn điểm nào sau đây cùng thuộc một đường tròn?
- A
- B
- C
- D
Xét ΔBNC có CN⊥AB mà D là trung điểm của BC nên DN=DC=DB(1) .
Xét ΔBMC có BM⊥AC mà D là trung điểm của BC nên BD=DM=DC(2) .
Từ (1) và (2) nên ta có BD=DC=DM=DN
Vậy 4 điểm B,C,M,N cùng thuộc đường tròn tâm D đường kính BC .
Câu 20: Cho hình vuông ABCD , O là giao điểm của hai đường chéo, OA=√2cm . Vẽ đường tròn tâm A bán kính 2cm . Khi đó ta có
- A
- B
- C
- D
OA=√2<2 nên điểm O nằm trong (A;2)
AB=2 nên điểm B nằm trên (A;2)
AD=2 nên điểm D nằm trên (A;2)
AC=2√2>2 nên điểm C nằm ngoài (A;2)
Câu 21: Cho hình chữ nhật ABCD có AB=12cm,BC=5cm . Tính bán kính đường tròn đi qua bốn đỉnh A,B,C,D .
- A
- B
- C
- D
Gọi I là giao hai đường chéo, ta có IA=IB=IC=ID (vì BD=AC và I là trung điểm mỗi đường)
Nên bốn điểm A,B,C,D cùng thuộc đường tròn tâm I bán kính R=AC2
Theo định lý Pytago trong tam giác vuông ABC ta có AC=√AB2+BC2=13 nên R=AC2=6,5cm .
Vậy bán kính cần tìm là R=6,5cm .
Câu 22: Trên mặt phẳng toạ độ Oxy , xác định vị trí tương đối của điểm A(−3;−4) và đường tròn tâm là gốc toạ độ O , bán kính R=3 .
- A
- B
- C
- D
Ta có OA=√(−3−0)2+(−4−0)2=5>3=R nên A nằm bên ngoài đường tròn tâm O bán kính R=3 .
Câu 23: Bán kính R của đường tròn đi qua cả bốn đỉnh của hình vuông ABCD cạnh 3cm là
- A
- B
- C
- D
Gọi O là giao hai đường chéo của hình vuông ABCD . Khi đó theo tính chất của hình vuông ta có OA=OB=OC=OD nên O là tâm đường tròn ngoại tiếp hình vuông ABCD , bán kính R=OA=AC2 .
Xét tam giác ABC vuông cân tại B ta có AC2=AB2+BC2=32+32=18⇒AC=3√2⇒R=3√22
Vậy R=3√22 .
Câu 24: Trên mặt phẳng toạ độ Oxy , xác định vị trí tương đối của điểm A(−1;−1) và đường tròn tâm là gốc toạ độ O , bán kính R=2 .
- A
- B
- C
- D
Ta có OA=√(−1−0)2+(−1−0)2=√2<2=R nên A nằm trong đường tròn tâm O bán kính R=2 .
Câu 25: Cho tam giác ABC vuông tại A , có AB=5cm;AC=12cm . Tính bán kính đường tròn ngoại tiếp tam giác ABC .
- A
- B
- C
- D
Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp là trung điểm cạnh huyền BC , bán kính là R=BC2 .
Theo định lý Pytago ta có BC=√AC2+AB2=13 nên bán kính R=132 .
Xem thêm các bài tiếp theo bên dưới