Dạng đồ thị hàm bậc 3
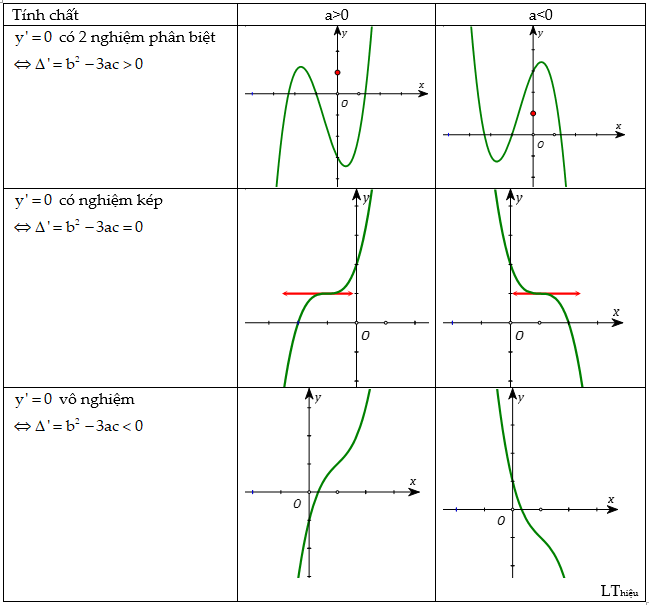
Lý thuyết về Dạng đồ thị hàm bậc 3
Dạng $y=ax^3+bx^2+cx+d, a\ne 0$
Hệ số d là tung độ giao điểm giữa đồ thị và $Oy$
Bài tập tự luyện có đáp án
Câu 1: Phương trình ${{x}^{3}}+3{{x}^{2}}-x-3=m$ có tối đa bao nhiêu nghiệm?
- A
- B
- C
- D
$y={{x}^{3}}+3{{x}^{2}}-x-3$ có $2$ cực trị nên phương trình ${{x}^{3}}+3{{x}^{2}}-x-3=m$có tối đa là $3$ nghiệm.
Câu 2: Phương trình ${{x}^{3}}-3{{x}^{2}}+3x-1=m$ có tối đa bao nhiêu nghiệm?
- A
- B
- C
- D
Hàm số $y={{x}^{3}}-3{{x}^{2}}+3x-1\left( C \right)$ luôn đồng biến trên R nên giao điểm với đường thẳng $y=m$ chỉ tại 1 điểm. Suy ra số nghiệm tối đa của phương trình là 1.
Câu 3: Đồ thị sau là của hàm số nào?


- A
- B
- C
- D
Đồ thị TCĐ $ x=-1 $ nên loại (I)
$ x=0,y=1 $ nên loại (II), (IV).
Câu 4: Đồ thị nào sau đây là đồ thị hàm bậc ba $y=a{{x}^{3}}+b{{x}^{2}}+cx+d\left( a>0 \right)$ và $y'=0$ có nghiệm kép?


- A
- B
- C
- D
Bảng các dạng đồ thị hàm số bậc ba SGK Giải tích 12 (CB) trang 35.
Câu 5: Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào ?


- A
- B
- C
- D
Dựa vào hình vẽ, ta thấy đây là đồ thị cảu hàm số bậc 3 và hệ số $a>0$.
Câu 6:  Đường cong ở hình bên là đồ thị của hàm số nào sau đây?
Đường cong ở hình bên là đồ thị của hàm số nào sau đây?
 Đường cong ở hình bên là đồ thị của hàm số nào sau đây?
Đường cong ở hình bên là đồ thị của hàm số nào sau đây?- A
- B
- C
- D
Phương pháp:
+ Dựa vào đồ thị hàm số để đưa ra nhận xét và chọn hàm số hợp lý.
Cách giải: Dựa vào đồ thị hàm số ta thấy đồ thị hàm số cắt trục hoành tại 4 điểm phân biệt, có 3 cực trị và nhận trục tung làm trục đối xứng nên đồ thị của hàm số là đồ thị của hàm trùng phương.
Câu 7: Hàm số nào có đồ thị như hình vẽ .


- A
- B
- C
- D
Từ đồ thị ta thấy đây là đồ thị của hàm bậc 3 $ y=a{ x ^ 3 }+b{ x ^ 2 }+cx+d $
Từ trái sang phải, đồ thị hàm số đi lên $ \Rightarrow a > 0 $ $ \Rightarrow $ loại phương án $ y=-x{{\left( x+1 \right)}^ 2 } $
Đồ thị hàm số đi qua điểm $ \left( -1;0 \right) $ $ \Rightarrow $ loại phương án $ y=x{{\left( x-1 \right)}^ 2 } $ .
Hàm số đạt cực đại tại $ x=-1 $ $ \Rightarrow $ chọn đáp án $ y=x{{\left( x+1 \right)}^ 2 } $.
Câu 8: Cho hàm số $ y=f\left( x \right) $ liên tục trên $ \mathbb{R} $ và có bảng biến thiên như sau:
 Tìm khẳng định đúng dưới đây?
Tìm khẳng định đúng dưới đây?
 Tìm khẳng định đúng dưới đây?
Tìm khẳng định đúng dưới đây?- A
- B
- C
- D
Hàm số đạt cực tiểu tại $ x=2 $ .
Câu 9: Bảng biến thiên ở bên là của hàm số nào ?


- A
- B
- C
- D
Từ trái sang phải đồ thị hàm số đi xuống $ \Rightarrow $ hệ số của $ { x ^ 3 } $ nhỏ hơn 0 $ \Rightarrow $ loại 2 phương án $ y={ x ^ 3 }-3{ x ^ 2 }-1 $ và $ y={ x ^ 3 }+3{ x ^ 2 }-1 $
Đồ thị hàm số đi qua điểm $ \left( 2;3 \right) $ $ \Rightarrow $ chọn phương án $ y=-{ x ^ 3 }+3{ x ^ 2 }-1 $
Câu 10: Hàm số $y={{x}^{3}}-3{{x}^{2}}+2$ có đồ thị là dạng nào trong bốn đường cong được vẽ dưới đây ?
- A
- B
- C
- D
Do hàm số $y={{x}^{3}}-3{{x}^{2}}+2$ có hệ số của ${{x}^{3}}$ là $a=1>0$.
Và có $y' = 0 \Leftrightarrow 3{x^2} - 6x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {x = 0}\\ {x = 2} \end{array}} \right. \Rightarrow \left[ {\begin{array}{*{20}{l}} {y\left( 0 \right) = 2}\\ {y\left( 2 \right) = - 2} \end{array}} \right.$
Nên 2 điểm cực trị nằm về hai phía của trục hoành.
Câu 11: Đồ thị hàm số $ y=\dfrac{3x+1}{x-1} $ có tâm đối xứng là
- A
- B
- C
- D
Tâm đối xứng của đồ thị hàm số bậc nhất trên bậc nhất chính là giao điểm của hai đường tiệm cận
Câu 12:  Cho hàm số $y=f\left( x \right)$ có đồ thị như hình bên.
Mệnh đề nào dưới đây đúng?
Cho hàm số $y=f\left( x \right)$ có đồ thị như hình bên.
Mệnh đề nào dưới đây đúng?
 Cho hàm số $y=f\left( x \right)$ có đồ thị như hình bên.
Mệnh đề nào dưới đây đúng?
Cho hàm số $y=f\left( x \right)$ có đồ thị như hình bên.
Mệnh đề nào dưới đây đúng?- A
- B
- C
- D
Hàm số đạt cực đại tại $ x=0 $ và đạt cực tiểu tại $ x=2. $
Câu 13: Cho hàm số $y=a{{x}^{3}}-2{{\text{x}}^{2}}-2x+d\left( a\ne 0 \right)$ có đồ thị như hình vẽ bên . Khẳng định đúng là:


- A
- B
- C
- D
Nhìn hình dạng đồ thị suy ra $a>0$ , đồ thị cắt trục $Oy$ tại điểm có tung độ dương nên $d>0$
Câu 14: Cho hàm số $y={{x}^{3}}-2$. Khẳng định nào đúng trong các khẳng định sau?
- A
- B
- C
- D
Vì $x\in \mathbb{Z}\Rightarrow y={{x}^{3}}-2\in \mathbb{Z}$
Vậy chọn khẳng định “Đồ thị hàm số có vô số điểm có tọa độ nguyên” đúng.
Câu 15: Hình vẽ dưới đây là đồ thị của hàm số nào ?


- A
- B
- C
- D
Từ đồ thị ta thấy đây là đồ thị của hàm bậc 3 $ y=a{ x ^ 3 }+b{ x ^ 2 }+cx+d $ $ \Rightarrow $ loại phương án $ y=\dfrac{3-3x}{1+x} $ và $ y=-{ x ^ 4 }-2{ x ^ 2 }+3 $.
Từ trái sang phải, đồ thị hàm số đi xuống $ \Rightarrow a < 0 $ $ \Rightarrow $ chọn đáp án là $ y=-{ x ^ 3 }-2x+3 $.
Câu 16: Hàm số $ y=-{{x}^{3}}+3{{x}^{2}}-1 $ có đồ thị nào trong các đồ thị dưới đây?


- A
- B
- C
- D
Do hệ số của $ {{x}^{3}} $ âm nên ta loại được Hình 3 và Hình 4.
Dựa vào công thức của hàm số ta có $ x=0\Rightarrow y=-1 $ nên đáp án là Hình 1.
Câu 17: Hình vẽ dưới đây là đồ thị của hàm số nào ?


- A
- B
- C
- D
Từ đồ thị ta thấy đây là đồ thị của hàm bậc 3 $ y=a{ x ^ 3 }+b{ x ^ 2 }+cx+d $
Từ trái sang phải, đồ thị hàm số đi lên $ \Rightarrow a > 0 $ $ \Rightarrow $ loại 2 phương án $ y=-{ x ^ 3 }+3x-2 $ và $ y=-{ x ^ 3 }+4x-3 $
Đồ thị hàm số đi qua điểm $ \left( 0;2 \right) $ $ \Rightarrow $ chọn đáp án là $ y={ x ^ 3 }-3x+2 $
Câu 18:  Tâm đối xứng của đồ thị hàm số cho trong hình bên là:
Tâm đối xứng của đồ thị hàm số cho trong hình bên là:
 Tâm đối xứng của đồ thị hàm số cho trong hình bên là:
Tâm đối xứng của đồ thị hàm số cho trong hình bên là:- A
- B
- C
- D
Đồ thị có tâm đối xứng là \(\left( -1;4 \right)\)
Câu 19: Đồ thị hình bên là của hàm số nào?


- A
- B
- C
- D
Từ đồ thị ta thấy, đây là đồ thị hàm trùng phương $ y=a{ x ^ 4 }+b{ x ^ 2 }+c $
Từ dáng đồ thị $ \Rightarrow a < 0 $ $ \Rightarrow $ sẽ chọn 1 trong 2 phương án là $ y=-{ x ^ 4 }+3{ x ^ 2 }+1 $ và $ y=-{ x ^ 4 }+2{ x ^ 2 }+1 $ .
Mà từ đồ thị ta thấy, hàm số đạt cực trị tại $ x=\pm 1 $ $ \Rightarrow $ chọn đáp án $ y=-{ x ^ 4 }+2{ x ^ 2 }+1 $ .
Xem thêm các bài tiếp theo bên dưới