Nhắc lại và bổ sung các khái niệm về hàm số
Lý thuyết về Nhắc lại và bổ sung các khái niệm về hàm số
1. Định nghĩa hàm số
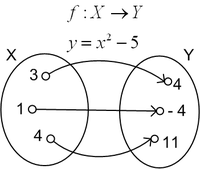
Cho X,Y là hai tập hợp số, hàm số f xác định trên X, nhận giá trị trong Y là một quy tắc cho tương ứng mỗi số x thuộc X với một số y duy nhất thuộc Y
Ví dụ: y=x2−5
– Khi x thay đổi mà y luôn nhận một giá trị không đổi thì y được gọi là một hàm hằng.
2. Đồ thị của hàm số
Tập hợp các điểm biểu diễn các cặp giá trị tương ứng (x;f(x)) trên mặt phẳng tọa độ được gọi là đồ thị của hàm số y=f(x).
Ví dụ: đồ thị hàm y=x2−1
3. Hàm số đồng biến, hàm số nghich biến
Cho hàm số y=f(x) xác định với mọi giá trị của xthuộc tập số thực R. Với x1;x2 tùy ý thuộc R:
a) Nếu x1<x2 mà f(x1)<f(x2) thì hàm số được gọi là hàm đồng biến.
Ví dụ: hàm số y=4x+3 là hàm số đồng biến
b) Nếu x1<x2 mà f(x1)>f(x2) thì hàm số được gọi là hàm nghịch biến.
Ví dụ: hàm số y=−2x+3 là hàm số nghịch biến.
Bài tập tự luyện có đáp án
Câu 1: Cho hai hàm số f(x)=5,5x có đồ thị (C) . Điểm nào sau đây thuộc đồ thị hàm số (C)
- A
- B
- C
- D
Lần lượt thay tọa độ các điểm M,N,P,Q vào hàm số f(x)=5,5x ta được
+) Với M(0;1) , thay x=0;y=1 ta được 1=5,5.0⇔1=0 (Vô lý) nên M∉(C)
+) Với N(2;11) , thay x=2;y=11 ta được 2.5,5=11⇔11=11 (luôn đúng) nên N∈(C)
+) Với P(−2;11) , thay x=−2;y=11 ta được 11=5,5.(−2)⇔11=−11 (Vô lý) nên P∉(C)
+) Với P(−2;12) , thay x=−2;y=12 ta được 12=5,5.(−2)⇔12=−11 (Vô lý) nên Q∉(C) .
Câu 2: Cho hai hàm số f(x)=−2x3 và h(x)=10−3x . So sánh f(−2) và h(−1)
- A
- B
- C
- D
Thay x=−2 vào hàm số f(x)=−2x3
ta được f(−2)=−2.(−2)3=16
Thay x=−1 vào hàm số h(x)=10−3x
ta được h(−1)=10−3(−1)=13
Nên f(−2)>h(−1) .
Câu 3: Cho hàm số f(x)=x3+x . Giá trị của f(x) tại x=2 là
- A
- B
- C
- D
Thay x=2 vào hàm số ta được f(2)=23+2=10 .
Câu 4: Hàm số y=1−4x là hàm số
- A
- B
- C
- D
TXĐ: D=R
Giả sử x1<x2 và x1,x2∈D
Ta có f(x1)=1−4x1;f(x2)=1−4x2
Xét hiệu H=f(x1)−f(x2)=1−4x1−(1−4x2)=1−4x1−1+4x2=4(x2−x1)>0 (vì x1<x2 )
Vậy y=1−4x là hàm số nghịch biến.
Câu 5: Cho hàm số y=mx−3m+2 . Tìm m để đồ thị hàm số đi qua điểm A(2;−3)
- A
- B
- C
- D
Thay x=2;y=−3 vào y=mx−3m+2 ta được m.2−3m+2=−3⇔−m=−5⇔m=5 .
Câu 6: Hàm số y=5x−16 là hàm số
- A
- B
- C
- D
TXĐ: D=R
Giả sử x1<x2 và x1,x2∈R .
Ta có f(x1)=5x1−16;f(x2)=5x2−16
Xét hiệu H=f(x1)−f(x2)=5x1−16−(5x2−16)
=5x1−16−5x2+16=5(x1−x2)<0 (vì x1<x2 )
Vậy y=5x−16 là hàm số đồng biến.
Câu 7: Cho hàm số f(x)=3x2+2x+1 . Giá trị của f(3)−2f(2) bằng
- A
- B
- C
- D
Thay x=3 vào hàm số ta được f(3)=3.32+2.3+1=34
Thay x=2 vào hàm số ta được f(2)=3.22+2.2+1=17
Suy ra f(3)−2f(2)=34−2.17=0 .
Câu 8: Đường thẳng đi qua điểm M(1;4) là
- A
- B
- C
- D
+) Thay x=1;y=4 vào 2x+y−3=0 ta được 2.1+4−3=3≠0
+) Thay x=1;y=4 vào y−5=0 ta được 4−5=−1≠0
+) Thay x=1;y=4 vào 4x−y=0 ta được 4.1−4=0
+) Thay x=1;y=4 vào 5x+3y−1=0 ta được 5.1+3.4−1=16≠0
Vậy đường thẳng d:4x−y=0 đi qua M(1;4) .
Câu 9: Đường thẳng đi qua điểm N(1;1) là
- A
- B
- C
- D
+) Thay x=1;y=1 vào 2x+y−3=0 ta được 2.1+1−3=0 nên điểm N thuộc đường thẳng 2x+y−3=0
+) Thay x=1;y=1 vào y−3=0 ta được 1−3=−2≠0
+) Thay x=1;y=1 vào 4x+2y=0 ta được 4.1+2.1=6≠0
+) Thay x=1;y=1 vào 5x+3y−1=0 ta được 5.1+3.1−1=7≠0
Vậy đường thẳng d:2x+y−3=0 đi qua N(1;1) .
Câu 10: Cho hai hàm số f(x)=−2x2 và g(x)=3x+5 . Giá trị của a để 12f(a)=g(a) là
- A
- B
- C
- D
Thay x=a vào hai hàm số đã cho ta được f(a)=−2a2;g(a)=3a+5 Khi đó 12f(a)=g(a)⇔12.(−2a2)=3a+5⇔−a2=3a+5⇔a2+3a+5=0 ⇔(a+32)2+114=0
(vô lý vì (a+32)2+114≥114>0;∀a )
Vậy không có giá trị của a thỏa mãn yêu cầu đề bài.
Câu 11: Cho hàm số y=(3−√2)x+1 . Khi đó f(3+√2) bằng
- A
- B
- C
- D
Ta có
f(3+√2)=(3−√2)(3+√2)+1=9−2+1=8
Câu 12: Cho hàm số y=f(x)=3x−1 . Khi đó giấ trị của a để f(a)+f(2+a)=0 là
- A
- B
- C
- D
Ta có
f(a)+f(2+a)=0⇔3a−1+3(2+a)−1=0⇔6a=−4⇒a=−23
Câu 13: Cho hàm số f(x)=3x có đồ thị (C) và các điểm M(1;1);O(0;0);P(−1;−3);Q(3;9);A(−2;6) . Có bao nhiêu điểm trong các điểm trên thuộc đồ thị hàm số (C)
- A
- B
- C
- D
Lần lượt thay tọa độ các điểm M,O,P,Q;A vào hàm số f(x)=3x ta được
+) Với M(1;1) , thay x=1;y=1 ta được 1=3.1⇔1=3 (vô lý) nên M∉(C) .
+) Với O(0;0) , thay x=0;y=0 ta được 0=3.0⇔0=0 (luôn đúng) nên O∈(C) .
+) Với P(−1;−3) , thay x=−1;y=−3 ta được −3=3.(−1)⇔−3=−3 (luôn đúng) nên P∈(C) .
+) Với Q(3;9) , thay x=3;y=9 ta được 9=3.3⇔9=9 (luôn đúng) nên Q∈(C) .
+) Với A(−2;6) , thay x=−2;y=6 ta được 6=(−2).3⇔6=−6 (vô lý) nên A∉(C) .
Vậy có ba điểm thuộc đồ thị (C) trong số các điểm đã cho.
Câu 14: Cho hàm số y=f(x)=2√x−1 . Khi đó f(1)+f(5) bằng
- A
- B
- C
- D
Ta có f(1)=2√1−1=0;f(5)=2.√5−1=4⇒f(1)+f(5)=4 vì 5≥0 và (5)2=25
Câu 15: Cho hàm số f(x)=3x−2 có đồ thị (C) . Điểm nào sau đây thuộc đồ thị hàm số (C) .
- A
- B
- C
- D
Lần lượt thay tọa độ các điểm M,N,P,Q vào hàm số f(x)=3x−2 ta được
+) Với M(0;1) , thay x=0;y=1 ta được 1=3.0−2⇔1=−2 (Vô lý) nên M∉(C)
+) Với N(2;3) , thay x=2;y=3 ta được 3=3.2−2⇔3=4 (Vô lý) nên N∉(C) .
+) Với P(−2;−8) , thay x=−2;y=−8 ta được −8=3.(−2)−2⇔−8=−8 (luôn đúng) nên P∈(C) .
+) Với Q(−2;0) , thay x=−2;y=0 ta được 0=3.(−2)−2⇔0=−8 (Vô lý) nên Q∉(C) .
Câu 16: Cho hàm số f(x)=x3−3x−2 . Giá trị của 2.f(3) bằng
- A
- B
- C
- D
Thay x=3 vào hàm số ta được f(3)=33−3.3−2=16
⇒2.f(3)=2.16=32 .
Câu 17: Cho hai hàm số f(x)=6x4 và h(x)=7−3x2 . So sánh f(−1) và h(23) ta được
- A
- B
- C
- D
Thay x=−1 vào hàm số f(x)=6x4 ta được f(−1)=6.(−1)4=6
Thay x=23 vào hàm số h(x)=7−3x2 ta được h(23)=7−3.232=6
Nên f(−1)=h(23) .
Câu 18: Cho hàm số y=5−m2x−2m−1 . Tìm m để hàm số nhận giá trị −5 khi x=2
- A
- B
- C
- D
Thay x=2;y=−5 vào y=5−m2x−2m−1
ta được −5=5−m2.2−2m−1⇔−3m+4=−5⇔−3m=−9⇔m=3.
Câu 19: Cho hàm số f(x)=2√x−2√x+4 . Tính f(4a2) với a≥0 .
- A
- B
- C
- D
Thay x=4a2 vào f(x)=2√x−2√x+4
ta được f(4a2)=2√4a2−2√4a2+4=2|2a|−2|2a|+4=4a−22a+4=2a−1a+2 (vì a≥0⇒|2a|=2a ).
Câu 20: Cho hàm số f(x)=√x+12√x+3 . Tính f(a2) với a<0
- A
- B
- C
- D
Thay x=a2 ta có f(a2)=|a|+12|a|+3 vì a<0 ta có:
f(a2)=1−a3−2a
Câu 21: Cho hàm số y=(2−3m)x−6 . Tìm m để đồ thị hàm số đi qua điểm A(−3;6)
- A
- B
- C
- D
Thay x=−3;y=6 vào y=(2−3m)x−6 ta được 6=(2−3m).(−3)−6⇔9m=18⇔m=2 .