Một số hệ thức về cạnh và góc trong tam giác vuông
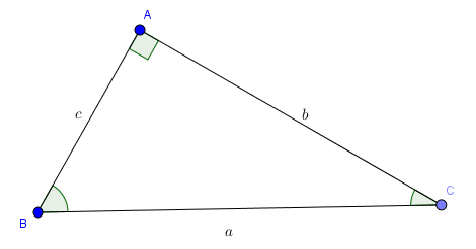
Lý thuyết về Một số hệ thức về cạnh và góc trong tam giác vuông
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
- Cạnh huyền nhân với sin góc đối hoặc nhân với cosin góc kề.
- Cạnh góc vuông kia nhân với tang góc đối hoặc nhân với cotan góc kề.
b=a⋅sinB=a⋅cosCb=c⋅tanB=c⋅cotCc=a⋅sinC=a⋅cosBc=b⋅tanC=b⋅cotB
Bài tập tự luyện có đáp án
Câu 1: Cho tam giác ABC có AB=12,AC=15 và ˆB=60∘ . Tính BC .
- A
- B
- C
- D
Kẻ đường cao AH .
Xét tam giác vuông ABH , ta có: BH=AB.cosB=AB.cos60∘=12.12=6
AH=AB.sinB=AB.sin60∘=12.√32=6√3 .
Áp dụng định lý Pytago vào tam giác vuông AHC ta có:
HC2=AC2−AH2=152−(6√3)2=117 .
Suy ra HC=3√13 .
Vậy BC=CH+HB=3√13+6 .
Câu 2: Trong tam giác vuông có góc nhọn a, câu nào sau đây sai
- A
- B
- C
- D
Ta luôn có 0<sinα<1,0<cosα<1 .
Câu 3: Cho tam giác ABC vuông tại A có AC=10cm,ˆC=30∘ . Độ dài các cạnh AB;BC lần lượt là
- A
- B
- C
- D
Xét tam giác ABC vuông tại A có
tanC=ABAC⇒AB=AC.tanC=10.tan30∘=10√33 ;
cosC=ACBC⇒BC=ACcosC=10√32=20√33 .
Vậy AB=10√33;BC=20√33 .
Câu 4: Cho tam giác ABC có BC=9cm,^ABC=50∘ và ^ACB=35∘ . Gọi N là chân đường vuông góc hạ từ A xuống cạnh BC . Độ dài AC gần nhất với giá trị nào dưới đây?
- A
- B
- C
- D
Đặt BN=x(0<x<9)⇒NC=9−x .
Xét tam giác ABN vuông tại N có AN=BN.tanB=x.tan50∘
Xét tam giác ACN vuông tại N có AN=CN.tanC=(9−x).tan35∘
Nên xtan50∘=(9−x).tan35∘⇒x≈3,33 (thoả mãn).
Khi đó AN=BN.tanB=3,33.tan35∘≈2,79 .
Xét tam giác ACN vuông tại N có sinC=ANAC⇒AC=ANsinC≈4,87
Câu 5: Cho tam giác ABC có BC=11cm,^ABC=40∘ và ^ACB=30∘ . Gọi N là chân đường vuông góc hạ từ A xuống cạnh BC . Độ dài AN gần nhất với giá trị nào dưới đây?
- A
- B
- C
- D
Đặt BN=x(0<x<11)⇒NC=11−x .
Xét tam giác ABN vuông tại N có AN=BN.tanB=x.tan40∘
Xét tam giác ACN vuông tại N có AN=CN.tanC=(11−x).tan30∘
Nên xtan40∘=(11−x).tan30∘⇒x≈4,48 (thoả mãn).
Khi đó AN=BN.tanB=4,48.tan40∘≈3,76(cm) .
Câu 6: Cho tam giác ABC vuông tại A có BC=12cm;ˆB=40∘ . Tính AC;ˆC (làm tròn đến chữ số thập phân thứ hai)
- A
- B
- C
- D
Xét tam giác ABC vuông tại A có
+ sinB=ACBC⇒AC=BC.sinB=12.sin40∘≈7,71 .
+ ˆA+ˆB+ˆC=180∘⇒ˆC=180∘−40∘−90∘=50∘ .
Vậy AC≈7,71;ˆC=50∘ .
Câu 7: Cho tam giác ABC vuông tại A có AC=20cm,ˆC=60∘ . Độ dài các cạnh AB;BC lần lượt là
- A
- B
- C
- D
Xét tam giác ABC vuông tại A có
tanC=ABAC⇒AB=AC.tanC=20.tan30∘=20√3 ;
cosC=ACBC⇒BC=ACcosC=2012=40 .
Vậy AB=20√3;BC=40 .
Câu 8: Cho tam giác ABC có AB=16,AC=14 và ˆB=60∘ . Tính BC .
- A
- B
- C
- D
Kẻ đường cao AH .
Xét tam giác vuông ABH , ta có: BH=AB.cosB=AB.cos60∘=16.12=8
AH=AB.sinB=AB.sin60∘=16.√32=8√3 .
Áp dụng định lý Pytago vào tam giác vuông AHC ta có:
HC2=AC2−AH2=142−(8√3)2=196−192=4 .
Suy ra HC=2 .
Vậy BC=CH+HB=2+8=10 .
Câu 9: Cho tam giác ABC vuông tại A có AC=7cm,AB=5cm . Tính BC;ˆC .
- A
- B
- C
- D
Xét tam giác ABC vuông tại A có
+ BC2=AB2+AC2=52+72=74⇒BC=√74(cm) .
+ tanC=ABAC=57⇒ˆC≈35∘32′
Vậy BC=√74(cm);ˆC≈35∘32′ .
Câu 10: Lúc 8 giờ sáng tia nắng mặt trời tạo với mặt đất một góc bằng 300. Bóng của cột cờ cao 10m trên mặt đất có chiều dài (đơn vị m, làm tròn đến phần trăm) là:


- A
- B
- C
- D
Gọi AB là chiều cao cột cờ, AC là bóng cột cờ trên mặt đất
Khi đó (ABC vuông tại A có AB = 10 m, ˆC=300
⇒AC=AB.cotC=10.cot300=10√3≈17,32 (m)
Câu 11: Cho tam giác ABC vuông tại A có BC=15cm,AB=12cm . Tính AC;ˆB .
- A
- B
- C
- D
Xét tam giác ABC vuông tại A có
+ BC2=AB2+AC2⇒AC=√BC2−AB2=√152−122=9(cm) .
+ sinB=ACBC=915=35 .
⇒ˆB≈36∘52′ .
Vậy AC=9(cm);ˆB≈36∘52′ .
Câu 12: Cho tam giác ABC có BC=11cm,^ABC=40∘ và ^ACB=30∘ . Gọi N là chân đường vuông góc hạ từ A xuống cạnh BC . Độ dài AC gần nhất với giá trị nào dưới đây?
- A
- B
- C
- D
Đặt BN=x(0<x<11)⇒NC=11−x .
Xét tam giác ABN vuông tại N có AN=BN.tanB=x.tan40∘
Xét tam giác ACN vuông tại N có AN=CN.tanC=(11−x).tan30∘
Nên xtan40∘=(11−x).tan30∘⇒x≈4,48 (thoả mãn).
Khi đó AN=BN.tanB=4,48.tan40∘≈3,76(cm)
Xét tam giác ACN vuông tại N có sinC=ANAC⇒AC=ANsinC=7,52
Câu 13: Cho tam giác ABC vuông tại A có BC=26cm,AB=10cm . Tính AC;ˆB (làm tròn đến độ).
- A
- B
- C
- D
Xét tam giác ABC vuông tại A có
+ BC2=AB2+AC2⇒AC=√BC2−AB2=√262−102=24(cm) .
+ sinB=ACBC=2426=1213⇒ˆB≈67∘ .
Vậy AC=24;ˆB≈67∘ .
Câu 14: Cho tam giác ABC có BC=9cm,^ABC=50∘ và ^ACB=35∘ . Gọi N là chân đường vuông góc hạ từ A xuống cạnh BC . Độ dài AN gần nhất với giá trị nào dưới đây?
- A
- B
- C
- D
Đặt BN=x(0<x<9)⇒NC=9−x .
Xét tam giác ABN vuông tại N có AN=BN.tanB=x.tan50∘
Xét tam giác ACN vuông tại N có AN=CN.tanC=(9−x).tan35∘
Nên xtan50∘=(9−x).tan35∘⇒x≈3,33 (thoả mãn).
Khi đó AN=BN.tanB=3,33.tan35∘≈2,79 .
Câu 15: Cho tam giác ABC có BC=9cm,^ABC=50∘ và ^ACB=35∘ . Gọi N là chân đường vuông góc hạ từ A xuống cạnh BC . Diện tích tam giác ABC gần nhất với giá trị nào dưới đây?
- A
- B
- C
- D
Đặt BN=x(0<x<9)⇒NC=9−x .
Xét tam giác ABN vuông tại N có AN=BN.tanB=x.tan50∘
Xét tam giác ACN vuông tại N có AN=CN.tanC=(9−x).tan35∘
Nên xtan50∘=(9−x).tan35∘⇒x≈3,33 (thoả mãn).
Khi đó AN=BN.tanB=3,33.tan35∘≈2,79 , nên SABC=AN.BC2=12,555cm2 .
Câu 16: Cho tam giác ABC vuông tại A có BC=15cm,ˆB=55∘ . Tính AC;ˆC (làm tròn đến chữ số thập phân thứ hai).
- A
- B
- C
- D
Xét tam giác ABC vuông tại A có
+ sinB=ACBC⇒AC=BC.sinB=15.sin55∘≈12,29 .
+ ˆA+ˆB+ˆC=180∘⇒ˆC=180∘−55∘−90∘=35∘ .
Vậy AC≈12,29;ˆC=35∘ .
Câu 17: Cho tam giác ABC có BC=11cm,^ABC=40∘ và ^ACB=30∘ . Gọi N là chân đường vuông góc hạ từ A xuống cạnh BC . Diện tích tam giác ABC gần nhất với giá trị nào dưới đây?
- A
- B
- C
- D
Đặt BN=x(0<x<11)⇒NC=11−x .
Xét tam giác ABN vuông tại N có AN=BN.tanB=x.tan40∘
Xét tam giác ACN vuông tại N có AN=CN.tanC=(11−x).tan30∘
Nên xtan40∘=(11−x).tan30∘⇒x≈4,48 (thoả mãn).
Khi đó AN=BN.tanB=4,48.tan40∘≈3,76(cm) , nên SABC=AN.BC2=20,68cm2 .
Xem thêm các bài tiếp theo bên dưới