Dạng toán xác định yếu tố song song giữa 2 đường
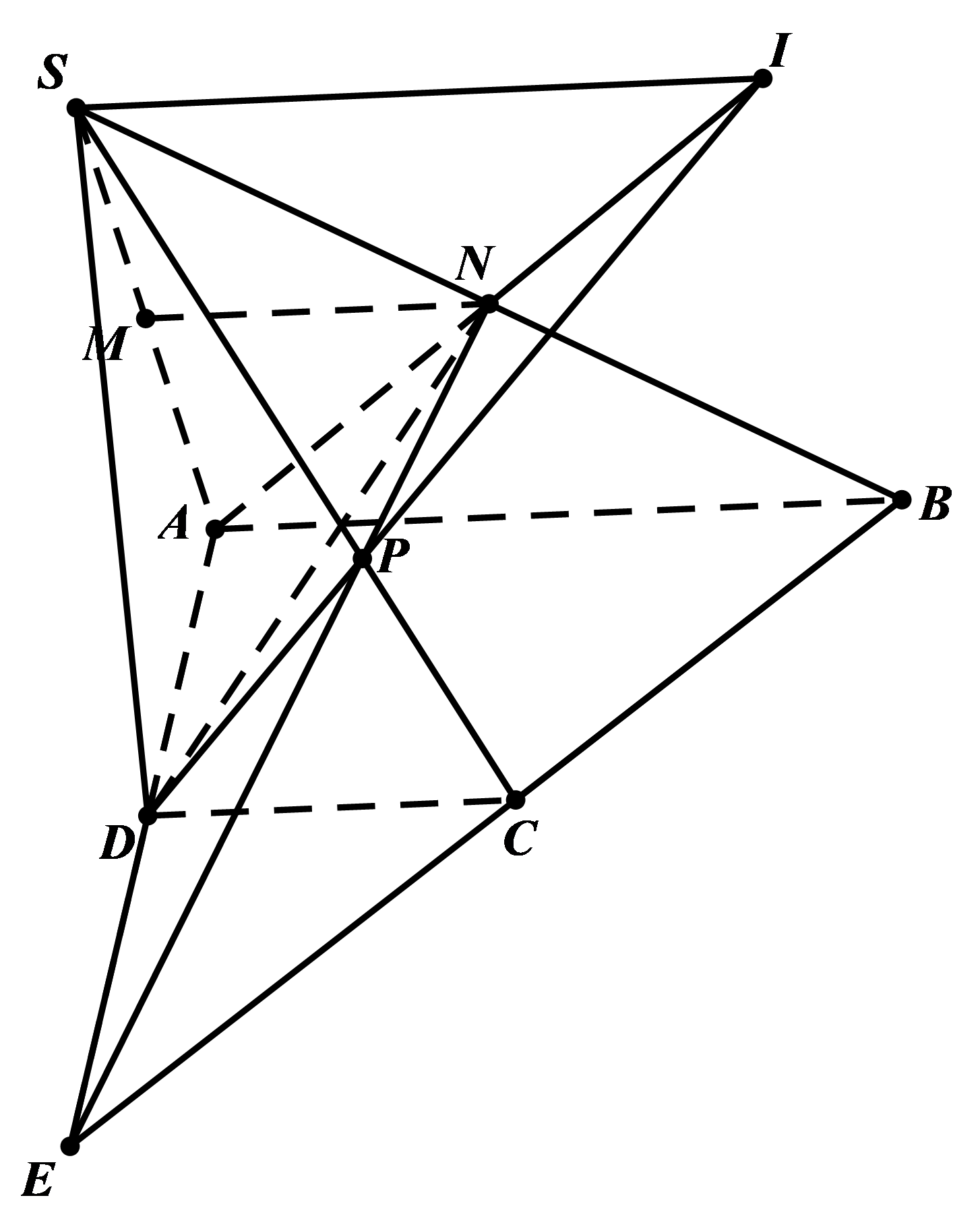
Lý thuyết về Dạng toán xác định yếu tố song song giữa 2 đường
Phương pháp chứng minh hai đường thẳng song song
Để chứng minh hai đường thẳng song song ta có thể làm theo một trong các cách sau:
- Chứng minh chúng cùng thuộc một mặt phẳng rồi dùng các phương pháp chứng minh hai đường thẳng song song trong mặt phẳng.
- Chứng minh hai đường thẳng đó cùng song song vơi đường thẳng thứ ba.
- Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
- Sử dụng định lí về giao tuyến của ba mặt phẳng.
Ví dụ: Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là một hình thang với đáy lớn \[AB\]. Gọi \[M,N\] lần lượt là trung điểm của \[SA\] và \[SB\]. Chứng minh rằng:
a)\[MN\] song song với \[CD\].
b)\[SI\] song song với \[CD\].
Lời giải:
a) Ta có \[MN\] là đường trung bình của tam giác \[SAB\] nên \[MN\parallel AB\].
Lại có \[ABCD\] là hình thang \[\Rightarrow AB//CD\].
Vậy \[\left\{ \begin{array}{l}
MN\parallel AB\\
CD\parallel AB
\end{array} \right. \Rightarrow MN\parallel CD\]
b) Trong \[\left( ABCD \right)\] gọi \[E=AD\cap BC\], trong \[\left( SCD \right)\] gọi \[P=SC\cap EN\].
Ta có \[E\in AD\subset \left( ADN \right)\] \[\Rightarrow EN\subset \left( AND \right)\Rightarrow P\in \left( ADN \right)\].
Vậy \[P=SC\cap \left( ADN \right)\].
Do \[I = AN \cap DP \Rightarrow \left\{ \begin{array}{l}
I \in AN\\
I \in DP
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
I \in \left( {SAB} \right)\\
I \in \left( {SCD} \right)
\end{array} \right. \Rightarrow SI = \left( {SAB} \right) \cap \left( {SCD} \right)\]
Ta có \[\left\{ \begin{array}{l}
AB \subset \left( {SAB} \right)\\
CD \subset \left( {SCD} \right)\\
AB\parallel CD\\
\left( {SAB} \right) \cap \left( {SCD} \right) = SI
\end{array} \right. \Rightarrow SI\parallel CD\]
Bài tập tự luyện có đáp án
Câu 1: Cho tứ diện $ABCD$. Các điểm $P,Q$ lần lượt là trung điểm của $AB$ và $CD$. Điểm $R$ nằm trên cạnh $BC$ sao cho $BR=2RC$. Gọi $S$ là giao điểm của$\left( PQR \right)$ và cạnh $AD$. Ta có
- A
- B
- C
- D

ĐỊNH LÝ MENELAUS
Giả sử đường thẳng$\Delta$cắt các cạnh (hoặc phần kéo dài)$BC,CA,AB$lần lượt tại$M,N,P$thì:
$\dfrac{MB}{MC}.\dfrac{NC}{NA}.\dfrac{PA}{PB}=1$
Áp dụng định lý để giải bài toán
Gọi$I=PR\cap AC$
Trong$\left( ACD \right)$gọi$S=QI\cap AD$thì
$S=AD\cap (PQR)$
Áp dụng định lý Menelaus trong$\Delta ABC$với cát tuyến$PRI$ta có:
$\dfrac{PA}{PB}.\dfrac{RB}{RC}.\dfrac{IC}{IA}=1\Rightarrow 1.2.\dfrac{IC}{IA}=1\Rightarrow \dfrac{IC}{IA}=\dfrac{1}{2}$
$\Rightarrow$C là trung điểm$AI$
Áp dụng định lý Menelaus trong$\Delta ACD$với cát tuyến$IQS$ta có:
$\dfrac{IC}{IA}.\dfrac{QD}{QC}.\dfrac{SA}{SD}=1\Rightarrow \dfrac{1}{2}.1.\dfrac{SA}{SD}=1\Rightarrow \dfrac{SA}{SD}=2$
$\Rightarrow SA=2SD$
Câu 2: Điền vào chỗ chấm để tạo thành câu hoàn chỉnh.
Gọi $G$ là trọng tâm của tứ diện $ABCD$. Đường thẳng đi qua $G$ và một đỉnh của tứ diện sẽ đi qua … của mặt đối diện với đỉnh ấy.
- A
- B
- C
- D

Gọi$N$là trung điểm của$CD$,$M=NG\cap AB$
Trong$\left( ABN \right)$gọi$A$là giao điểm của$AG$với trung tuyến$BN$của$\Delta BCD$. Ta chứng minh:
$AB=2AN$
Áp dụng định lý Menelaus trong$\Delta BMN$với cát tuyến$AGA$ta có:
$\dfrac{AM}{AB}.\dfrac{GN}{GM}.\dfrac{A'B}{A'N}=1$
$\Rightarrow \dfrac{1}{2}.1.\dfrac{A'B}{A'N}=1\Rightarrow \dfrac{A'B}{A'N}=2\Rightarrow A'B=2A'N$
Vậy$A$là trọng tâm của$\Delta$$ BCD$
Tương tự$BG,CG,DG$lần lượt đi qua trọng tâm$B,C,D$của tam giác$ACD,ABD,ABC$.
Câu 3: Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành. Gọi \[H\] và \[K\] lần lượt là các trung điểm của cạnh bên \[SA\] và \[SB\]. Cho điểm \[M\] nằm trên cạnh \[SC\] không trùng với \[S\]. Cho \[{ d _ 1 }=(HKM)\cap (SDC)\], \[{ d _ 2 }=(SAB)\cap (SCD)\], \[{ d _ 3 }=(SAD)\cap (SBC)\]. Ta có:
1.\[{ d _ 1 }//{ d _ 2 }\]
2.\[{ d _ 1 }//{ d _ 3 }\]
3.\[HK//CD\]
4.\[{ d _ 2 }//{ d _ 3 }\]
- A
- B
- C
- D

+ Chứng minh$HK//CD$
H, K là trung điểm$SA, SB$$ \Rightarrow$HK là đường trung bình trong$\Delta SAB\Rightarrow$$ HK//AB$
Mà$AB//CD~\Rightarrow HK//CD$
+ Ta có:$\left\{ \begin{align} & M\in (HKM)\cap (SDC) \\ & HK//CD \\ \end{align} \right.$
$\Rightarrow (HKM)\cap (SDC)={ d _ 1 }$đi qua M và song song với CD
+ Ta có$\left\{ \begin{align} & S\in (SAB)\cap (SCD) \\ & AB//CD \\ \end{align} \right.$
$\Rightarrow (SAB)\cap (SCD)={ d _ 2 }$đi qua S và song song với CD
+ Chứng minh tương tự ta được$(SAD)\cap (SCB)={ d _ 3 }$đi qua S và song song với AD
$\Rightarrow { d _ 1 }//{ d _ 2 }$
Câu 4: Cho hình bình hành$ABCD$. Qua$A, B, C, D$lần lượt vẽ bốn nửa đương thẳng$Ax, By, Cz, Dt$ở cùng phía đối với mặt phẳng$\left( ABCD \right)$, song song với nhau và không nằm trong$(ABCD)$. Một mặt phẳng$(\beta )$lần lượt cắt$Ax, By, Cz v\grave a Dt$tại$A, B, C v\grave a D$. Gọi$I=AC\cap BD,J=A'C'\cap B'D'$. Ta có: $\begin{align} & 1.IJ//AA' \\ & 2.IJ//BB' \\ & 3.IJ//CC' \\ & 4.IJ//DD' \\ & 5.IJ=\dfrac{AA'+CC'} 2 \\ & 6.IJ=\dfrac{BB'+DD'} 2 \\ \end{align}$
Số phát biểu sai là:
$\begin{align} & 1.IJ//AA' \\ & 2.IJ//BB' \\ & 3.IJ//CC' \\ & 4.IJ//DD' \\ & 5.IJ=\dfrac{AA'+CC'} 2 \\ & 6.IJ=\dfrac{BB'+DD'} 2 \\ \end{align}$
Số phát biểu sai là:
- A
- B
- C
- D

+$ABDC$là hình bình hành$\Rightarrow$$ AB//DC$(1)
Theo giả thiết$Ax//Dt$(2)
Từ (1) và (2)$\Rightarrow$mặt phẳng$\left( Ax,By \right)$song song với mặt phẳng$\left( Cz,Dt \right)$
+ Do$\left( Ax,By \right)//\left( Cz,Dt \right)$$ \Rightarrow$$ A'B'//DC.$
Tương tự, ta có:$AD//BC$
$\Rightarrow$tứ giác$ABCD$là hình bình hành,
Ta có: I là giao của$ACv\grave a DB$và J là giao của$A'C'v\grave a B'D'$
$\Rightarrow$J là trung điểm của$AC$và I là trung điểm của$AC$.
Mặt khác$Ax//Cz$nên tứ giác$ACCA$là hình thang
$\Rightarrow$$ IJ//AA//BB'//CC'//DD'$
+$IJ$là đường trung bình các hình thang$ACC'A'$và$DBB'D'$nên ta có:
$IJ=\dfrac{AA'+CC'} 2 =\dfrac{BB'+DD'} 2$
Câu 5: Cho hình hộp$ABCD.{ A _ 1 }{ B _ 1 }{ C _ 1 }{ D _ 1 }$. Điểm I thuộc đường chéo${ B _ 1 }D$và điểm J thuộc đường chéo$AC$sao cho$IJ$//$B{ C _ 1 }$. Tính tỉ số$\dfrac{ID}{I{ B _ 1 }}$
- A
- B
- C
- D

Giả sử tìm được$I\in { B _ 1 }D$,$J\in AC$sao cho$B{ C _ 1 }//\text{IJ}$.
+ Kẻ${ B _ 1 }{ B _ 1 }'//{ C _ 1 }B$cắt BC tại${ B _ 1 }'$
+$J={ B _ 1 }'D\cap AC$
+ Trong$({ B _ 1 }{ B _ 1 }'D)$kẻ$JI$song song với${ B _ 1 }{ B _ 1 }'$cắt${ B _ 1 }D$tại I
Dễ thấy${ B _ 1 }'$thuộc đường thẳng BC và$AD=\dfrac{1}{2} { B _ 1 }'C$
Từ đó suy ra:$\dfrac{ID}{I{ B _ 1 }}=\dfrac{ID}{J{ B _ 1 }'}=\dfrac{AD}{{ B _ 1 }'C}=\dfrac{1}{2}$
Vậy ta có:$\dfrac{ID}{I{ B _ 1 }}=\dfrac{1}{2}$
Câu 6: Cho tứ diện \[ABCD\]. Gọi \[M,N\] lần lượt là trung điểm của các cạnh \[AB,CD\] và \[G\] là trung điểm của đoạn \[MN\].\[A'=AG\cap (BCD)\]. Qua \[M\] kẻ đường thẳng\[Mx\]song song với \[AA'\] và \[Mx\] cắt \[\left( BCD \right)\] tại \[M'\]. Cho các khẳng định
1. \[B,M',A'\] thẳng hàng
2. $BM'=M'A'=A'N$
3. \[GA=3GA'\]
Số khẳng định đúng là
- A
- B
- C
- D

+ Chứng minh thẳng hàng
Từ M kẻ đường thẳng$Mx$song song với$AA.$
$Mx\subset \left( ABN \right)$và$Mx$$ \cap$$ BN=M$
$\Rightarrow$M' thuộc$BN$
$\Rightarrow$$ B,M,A$thẳng hàng
+ Chứng minh$BM'=M'A'=A'N$
$MM$là đường trung bình của tam giác$ABA$nên$BM=MA$(1)
$GA$là đường trung bình của tam giác$MMN$nên$MA=AN$(2)
$\Rightarrow \dfrac{A'B}{BN}=\dfrac{2}{3}$
$BN$là đường trung tuyến và$\dfrac{A'B}{BN}=\dfrac{2}{3}$
$\Rightarrow$A' là trọng tâm$\Delta$$ BCD$
$\Rightarrow$$ BM=MA=AN$
+ Áp dụng chứng minh trên ta có:
$\Delta$$ MMN:2GA=MM$
$\Delta$$ BAA:2MM=AA$
$\Rightarrow$$ GA=3GA.$
Câu 7: Cho hình chóp$S.ABCD$với đáy$ABCD$là hình thang với cạnh đáy$AB$ và $CD$.
Gọi$M,N,P$lần lượt là trung điểm các cạnh$SA,SB,SC$.$I\in (SAB)\cap (SCD)$sao cho$SI=AB$. Cho các nhận xét:
- $MN \parallel CD$
- $SI \parallel AB$
- $SI \parallel CD$
- $SABI$là hình bình hành
Số nhận xét đúng là:
- $MN \parallel CD$
- $SI \parallel AB$
- $SI \parallel CD$
- $SABI$là hình bình hành
- A
- B
- C
- D

+ Chứng minh :$MN//CD$:
Trong tam giác$SAB$, ta có :$MN//AB$Mà$AB//CD$($ABCD$là hình thang )
Vậy :$MN//CD$
+ Chứng minh :$SI//AB//CD$.
Ta có :$\left\{ \begin{align} & SI=(SAB)\cap (SCD) \\ & AB\in (SAB) \\ & CD\in (SCD) \\ & AB//CD \\ \end{align} \right.$$ \Rightarrow SI//AB//CD$( theo định lí 2)
Lại có:$SI=AB\Rightarrow SI\underset{==}{\mathop{//}}\,AB$
Vậy : tứ giác$SABI$là hình bình hành
Câu 8: Cho hình lăng trụ tam giác $ABC.A'B'C'$. Gọi $G,G'$ lần lượt là trọng tâm của tam giác $ABC$và$A'B'C'$. Một mặt phẳng $(\alpha )$ cắt các cạnh $AA',BB',CC',GG'$ lần lượt tại ${ A _ 1 },{ B _ 1 },{ C _ 1 },{ G _ 1 }$. Khi đó, khẳng định nào sau đây sai?
- A
- B
- C
- D

+ Gọi$I,I'$lần lượt là trung điểm của các cạnh$BC,B'C'$ thì rõ ràng$II'$song song và bằng$AA'$nên tứ giác $AII'A'$ là hình bình hành, do đó$AI$song song và bằng$A'I'$.
Ta cũng có$AG=\dfrac{2}{3} AI,A'G'=\dfrac{2}{3} A'I'$, mà$AI=A'I'$
Suy ra$AG$song song và bằng$A'G'$
Vậy tứ giác$AGG'A'$là hình bình hành
Do đó, $GG'$ song song và bằng $AA'$
+${ B _ 1 }{ C _ 1 }$cắt$II'$tại${ I _ 1 }$thì${ I _ 1 }$là trung điểm của${ B _ 1 }{ C _ 1 }$
Vì${ G _ 1 }$thuộc${ A _ 1 }{ I _ 1 }$và$A {{ A }_ 1 }//G{ G _ 1 }//I{ I _ 1 }$nên:
$\dfrac{{ G _ 1 }{ A _ 1 }}{{ A _ 1 }{ I _ 1 }}=\dfrac{GA}{AI}=\dfrac{2}{3}$
Vậy${ G _ 1 }$là trọng tâm$\Delta { A _ 1 }{ B _ 1 }{ C _ 1 }$
Câu 9: Cho tứ diện$ABCD$. Gọi $I; J$ lần lượt là trọng tâm các tam giác $ABC$ và $ ABD$. Ta có
- A
- B
- C
- D

Gọi E là trung điểm$AB$
Ta có :$\left\{ \begin{align} & I\in CE \\ & J\in DE \\ \end{align} \right.$$ \Rightarrow$$ IJv\grave a CD$đồng phẳng
Do đó :$\dfrac{EI}{EC}=\dfrac{\text{EJ}}{ED}=\dfrac{1}{3}$(tính chất trọng tâm)
Vậy :$IJ//CD$.
Câu 10: Cho hình chóp\[S.ABCD.M,N\]là hai điểm trên\[AB,CD\]. Mặt phẳng \[(\alpha )\] qua $MN$ và song song $SA$.
Tìm điếu kiện của\[MN\]để thiểt diện tạo bởi mặt phẳng $\left(\alpha\right)$ và hình chóp là một hình thang
- A
- B
- C
- D

Ta có :$MPQN$là hình thang$\Rightarrow$$ \left[ \begin{align} & MP//QN \\ & MN//PQ \\ \end{align} \right.\begin{matrix} {} \\ {} \\ \end{matrix}\begin{matrix} {} \\ {} \\ \end{matrix}\begin{matrix} {} \\ {} \\ \end{matrix}\begin{matrix} (1) \\ (2) \\ \end{matrix}$
Xét (1) ,ta có$\left\{ \begin{align} & \text{SA // MP} \\ & \text{MP//QN} \\ \end{align} \right.\begin{matrix} {} & {} \\ \end{matrix}\Rightarrow \begin{matrix} {} & SA//QN \\ \end{matrix}$
Do đó :$\left\{ \begin{align} & SA//QN \\ & QN\subset (SCD) \\ \end{align} \right.\begin{matrix} {} & {} \\ \end{matrix}\Rightarrow \begin{matrix} {} & SA//(SCD) \\ \end{matrix}$( vô lí )
Xét (2) ,ta có$\left\{ \begin{align} & \text{BC}=\text{(ABCD)}\cap \text{(SBC)} \\ & \text{MN}\subset \text{(ABCD)} \\ & \text{PQ}\subset \text{(SBC)} \\ \end{align} \right.\begin{matrix} {} & {} \\ \end{matrix}\Rightarrow \begin{matrix} {} & MN//BC \\ \end{matrix}$.
Ngược lại, nếu$MN//BC$thì$\left\{ \begin{align} & PQ=\alpha \cap (SBC) \\ & MB\subset (\alpha ) \\ & BC\subset (SBC) \\ \end{align} \right.\begin{matrix} {} & {} \\ \end{matrix}\Rightarrow \begin{matrix} {} & {} \\ \end{matrix}MN//PQ$
Vậy để thiết diện là hình thang thì$MN//BC$.
Câu 11: Cho hình hộp$ABCD.A'B'C'D'$. Trên ba cạnh$AB,DD',B'C'$lần lượt lấy ba điểm$M,N,P$không trùng với các đỉnh sao cho$\dfrac{AM}{AB}=\dfrac{D'N}{D'D}=\dfrac{B'P}{B'C'}$. E là điểm thuộc$BB'$sao cho$ME//AB'$. Ta có:
$\begin{array}{*{35} l } 1.EP//AD' \\ 2.EP//BC' \\ 3.EN//BD \\ \end{array}$
4. Thiết diện khi cắt hình hộp bởi$\left( MNP \right)$là ngũ giác.
Các phát biểu đúng là
- A
- B
- C
- D

+ Kẻ$ME//AB$(1)
Ta có:$\dfrac{B'E}{B'B}=\dfrac{AM}{AB}\Rightarrow \dfrac{B'E}{B'B}=\dfrac{B'P}{B'C'}\Rightarrow EP//BC'\Rightarrow EP//AD'(2)$
Từ (1) và (2) suy ra$\left( MEP \right)//\left( ABD \right)$(3)
Rõ ràng$DN=BE$nên$EN//BD$.
+ Từ P kẻ$PF$song song với$BD$, từ N kẻ$NK$song song với$AD$cắt$AD$tại K.
Thiết diện là lục giác$MEPFNK$có các cạnh đối song song.