Tính chất của tính vô hướng Định lí Với ba vectơ $\overright
Lý thuyết về Tính chất của tính vô hướng Định lí Với ba vectơ $\overright
Tính chất của tính vô hướng
Định lí
Với ba vectơ $\overrightarrow{a,}\overrightarrow{b},\overrightarrow{c}$tuỳ ý và mọi số thưc k ,ta có
1)$\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{a}$ (tính chất giao hoán);
2)$\overrightarrow{a}.\overrightarrow{b}=0\Leftrightarrow \overrightarrow{a}\bot \overrightarrow{b}$
3)$\left( k\overrightarrow{a} \right).\overrightarrow{b}=\overrightarrow{a}\left( k\overrightarrow{b} \right)=k\left( \overrightarrow{a}.\overrightarrow{b} \right)$
4) $\overrightarrow{a}.\left( \overrightarrow{b}+\overrightarrow{c} \right)=\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{a}.\overrightarrow{c}$ (tính chất phân phối đối với phép cộng);
$\overrightarrow{a}.\left( \overrightarrow{b}-\overrightarrow{c} \right)=\overrightarrow{a}.\overrightarrow{b}-\overrightarrow{a}.\overrightarrow{c}$ (tính chất phân phối đối với phép trừ);
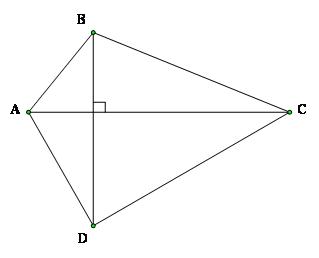
Bài toán 1: Cho tứ giác ABCD
a. Chứng minh rằng: $A{{B}^{2}}+C{{D}^{2}}=B{{C}^{2}}+A{{D}^{2}}+2\overrightarrow{CA}.\overrightarrow{BD}$
b. Chứng minh: Điều kiện cần và đủ để tứ giác có hai đường thẳng chéo vuông góc là tổng bình phương các cặp cạnh đối diện bằng nhau.
Giải
a, Ta có
$\begin{align}& A{{B}^{2}}+C{{D}^{2}}-B{{C}^{2}}-A{{D}^{2}} \\ & ={{\left( \overrightarrow{CB}-\overrightarrow{CA} \right)}^{2}}+C{{D}^{2}}-C{{B}^{2}}-{{\left( \overrightarrow{CD}-\overrightarrow{CA} \right)}^{2}} \\ & =-2\overrightarrow{CB}.\overrightarrow{CA}+2\overrightarrow{CD}.\overrightarrow{CA} \\ & =2\overrightarrow{CA}.\left( \overrightarrow{CD}-\overrightarrow{CB} \right)=2\overrightarrow{CA}.\overrightarrow{BD} \\ \end{align}$
Từ đó suy ra điều phải chứng minh
b. Từ a ta có: $CA\bot BD\Leftrightarrow \overrightarrow{CA}.\overrightarrow{BD}\Leftrightarrow A{{B}^{2}}+C{{D}^{2}}=B{{C}^{2}}+A{{D}^{2}}$
Chú ý:
1) Cho 2 vecto $\overrightarrow{OA},\overrightarrow{OB}$ . Gọi $B’$ là hình chiếu của $B$ trên đường thằng $OA.$ Khi đó:
- Vecto $\overrightarrow{OB'}$ gọi là hình chiếu của vecto $\overrightarrow{OB}$ trên đường thằng $OA$
- Công thức $\overrightarrow{OA}.\overrightarrow{OB}=\overrightarrow{OA}'.\overrightarrow{OB}'$ gọi là công thức hình chiếu
2) Cho đường tròn (O;R) và điểm M cố định. Một đường thẳng thay đổi đi qua M, cắt đường tròn đó tại 2 điểm A và B.
Khi đó, giá trị không đổi $\overrightarrow{MA}.\overrightarrow{MB}={{d}^{2}}-{{R}^{2}}\left( d=MO \right)$ gọi là phương tích của điểm M đối với đường tròn (O) và kí hiệu là ${{\left( P \right)}_{M/\left( O \right)}}$
${{\left( P \right)}_{M/\left( O \right)}}=\overrightarrow{MA}.\overrightarrow{MB}={{d}^{2}}-{{R}^{2}}\left( d=MO \right)$
3) Khi điểm M nằm ngoài đường tròn (O), MT là tiếp tuyến của đường tròn đó ( T là tiếp điểm) thì ${{\left( P \right)}_{M/\left( O \right)}}={{\overrightarrow{MT}}^{2}}=M{{T}^{2}}$
Bài tập tự luyện có đáp án
Câu 1: Trong mặt phẳng $ \left( O;\overrightarrow{i},\overrightarrow{j} \right) $ cho 2 vectơ : $ \overrightarrow{a}=3\overrightarrow{i}+6\overrightarrow{j} $ và $ \overrightarrow{b}=8\overrightarrow{i}-4\overrightarrow{j.} $ Kết luận nào sau đây sai?
- A
- B
- C
- D
$ \overrightarrow{a}=\left( 3;6 \right);\overrightarrow{b}=\left( 8;-4 \right) $
Phương án (I): $ \overrightarrow{a}.\overrightarrow{b}=24-24=0 $ nên loại (I)
Phương án (II): $ \overrightarrow{a}.\overrightarrow{b}=0 $ suy ra $ \overrightarrow{a} $ vuông góc $ \overrightarrow{b} $ nên loại (II)
Phương án (III): $ \left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right|=\sqrt[{}]{{{3}^{2}}+{{6}^{2}}}.\sqrt[{}]{{{8}^{2}}+{{\left( -4 \right)}^{2}}}\ne 0 $ nên chọn (III)
Câu 2: Cho các vectơ $ \overrightarrow{a}=\left( 1;-3 \right),\,\,\overrightarrow{b}=\left( 2;5 \right) $ . Tính tích vô hướng của $ \overrightarrow{a}\left( \overrightarrow{a}+4\overrightarrow{b} \right) $
- A
- B
- C
- D
Ta có $ \overrightarrow{a}.\overrightarrow{a}=10 $ , $ \overrightarrow{a}.\overrightarrow{b}=-13 $ suy ra $ \overrightarrow{a}\left( \overrightarrow{a}+4\overrightarrow{b} \right)=-42 $
Câu 3: Trong mặt phẳng $ Oxy $ , cho $ \overrightarrow{a}=\left( 2;-1 \right) $ và $ \overrightarrow{b}=\left( -3;4 \right) $ . Khẳng định nào sau đây là sai ?
- A
- B
- C
- D
Ta có $ \left| \overrightarrow{a} \right|=\sqrt{{{2}^{2}}+{{\left( -1 \right)}^{2}}}=\sqrt{5} $
$ \left| \overrightarrow{b} \right|=\sqrt{{{\left( -3 \right)}^{2}}+{{4}^{2}}}=5 $
$ \overrightarrow{a}.\overrightarrow{b}=2.\left( -3 \right)+\left( -1 \right).4=-10\ne 0 $
Câu 4: Cặp vectơ nào sau đây vuông góc?
- A
- B
- C
- D
Phương án 1: $ \overrightarrow{a}.\overrightarrow{b}=2.\left( -3 \right)+\left( -1 \right).4=-10\ne 0 $
Phương án 2: $ \overrightarrow{a}.\overrightarrow{b}=3.\left( -3 \right)+\left( -4 \right).4\ne 0 $
Phương án 3: $ \overrightarrow{a}.\overrightarrow{b}=-2.\left( -6 \right)-3.4=0\Rightarrow \overrightarrow{a}\bot \overrightarrow{b} $
Phương án 4: $ \overrightarrow{a}.\overrightarrow{b}=7.3+\left( -3 \right).\left( -7 \right)=42\ne 0 $
Câu 5: Cho $ \overrightarrow{a} $ và $ \overrightarrow{b} $ là hai vectơ cùng hướng và đều khác vectơ $ \overrightarrow{0} $ . Trong các kết quả sau đây, hãy chọn kết quả đúng:
- A
- B
- C
- D
Ta thấy vế trái của 4 phương án giống nhau.
Bài toán cho $ \overrightarrow{a} $ và $ \overrightarrow{b} $ là hai vectơ cùng hướng và đều khác vectơ $ \overrightarrow{0} $ suy ra $ \left( \overrightarrow{a},\overrightarrow{b} \right)={{0}^{0}} $
Do đó $ \overrightarrow{a}.\overrightarrow{b}=\left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right|.\cos {{0}^{\text{o}}}=\left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right| $