Hình thang cân
Lý thuyết về Hình thang cân
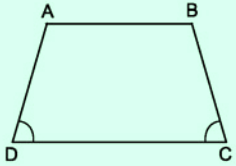
Định nghĩa: Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
ABCD là hình thang cân có hai đáy là AB và CD ⇔ {AB∥CD[ˆC=ˆDˆA=ˆB
Tính chất.
- Trong hình thang cân, hai cạnh bên bằng nhau.
- Trong hình thang cân, hai đường chéo bằng nhau.
Dấu hiệu nhận biết
- Hình thang có hai đường chéo bằng nhau là hình thang cân
- Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
- Hình thang có hai đường chéo bằng nhau là hình thang cân.
Bài tập tự luyện có đáp án
Câu 1: Cho hình thang cân ABCD (AB//CD) có ˆC=600 , DB là tia phân giác góc ˆD . Biết chu vi hình thang bằng 30cm, giá trị của AB bằng
- A
- B
- C
- D

Đặt AB=x(cm)
ˆC=ˆD=2ˆD1=600⇒^D1=^D2=300
^D1=^B1 (so le trong) ⇒^D2=^B1⇒ΔABD cân ở A ⇒AB=AD=BC=x(cm) .
^DBC=1800−^D1−ˆC=900 ⇒ΔDBC vuông ở B. BC là cạnh đối diện góc 300 ⇒BC=12DC⇒DC=2BC=2x
⇒ chu vi hình thang bằng AB+BC+CD+DA=5x=30⇒x=6cm .
Vậy AB=6(m)
Câu 2: Cho hình thang cân ABCD với hai đáy AB∥CD có ˆA=70∘. Khẳng định nào dưới đây đúng?
- A
- B
- C
- D
Do hình thang cân với hai đáy AB,CD nên ta có: ˆA=ˆB=70∘ ⇒ ˆC=ˆD=110∘
Câu 3: Chọn khẳng định sai trong các khẳng định sau
- A
- B
- C
- D
Hình thang không có tâm đối xứng.
Câu 4: Hình thang cân ABCD (AB // CD) có ˆA=700 . Khẳng định nào dưới đây là đúng?
- A
- B
- C
- D
Vì hình thang ABCD là hình thang cân có AB//CD
Nên ˆC=ˆD ( tính chất)
Mà ˆA và ˆD trong cùng phía
⇒ˆA+ˆD=ˆA+ˆC=1800⇒ˆD=ˆC=110o.
Câu 5: Khẳng định sai là
- A
- B
- C
- D
Hình thang có hai cạnh bên bằng nhau chưa chắc đã hình thang cân. (Xem hình vẽ)

Xem thêm các bài tiếp theo bên dưới