Định luật Sác - lơ
Lý thuyết về Định luật Sác - lơ
Quá trình đẳng tích là quá trình biến đổi trạng thái khi thể tích không đổi.
Trong quá trình đẳng tích của một lượng khí nhất định, áp suất tỉ lệ thuận với nhiệt độ tuyệt đối.
p˜ T=pT hằng số hay p1T1=p2T2=.....
p1;p2 là áp suất của khí lí tưởng ở trạng thái 1 và trạng thái 2
T1;T2 là nhiệt độ của khí ở trạng thái 1 và trạng thái 2
Chú ý: Nhiệt độ ở thang nhiệt giai Kelvin (0oC=273K )
Bài tập tự luyện có đáp án
Câu 1: Hiện tượng nào sau đây có liên quan đến định luật Sác-lo?
- A
- B
- C
- D
"Xe đạp để ngoài nắng có thể bị nổ lốp." có liên quan đến định luật Sác-lo.
lốp xe với thể tích không đổi, khi ngoài nawgs nhiệt độ tăng, áp suất cũng tăng, có thể làm nổ lốp.Câu 2: Đồ thị nào trên hình biểu diễn không đúng quá trình biến đổi đẳng tích?
- A
- B
- C
- D
Do đây là quá trình đẳng tích nên PT=const , nên trong hệ trục tọa độ (p,T) thì đồ thị phải có dạng đường thẳng đi qua gốc của hệ trục tọa độ
Câu 3: Hiện tượng nào dưới đây áp dụng được định luật Sác-lơ?
- A
- B
- C
- D
Định luật Sác-lơ áp dụng cho quá trình đẳng tích, dễ nhận thấy trên các đáp án chỉ có một phương án có thể tích cố định.
Câu 4: Trong quá trình chuyển trạng thái đẳng tích của một khối khí, khối lượng riêng của nó.
- A
- B
- C
- D
Với lượng khí nhất định, thể tích không đổi thì mật độ phân tử của chất khí không đổi, hay khối lượng riêng của nó không thay đổi.
Câu 5: Quá trình biến đổi trạng thái của một lượng khí xác định trong đó thể tích được giữ không đổi gọi là quá trình
- A
- B
- C
- D
Quá trình biến đổi trạng thái của một lượng khí xác định trong đó thể tích được giữ không đổi gọi là quá trình đẳng tích.
Câu 6: Giữ thể tích của một khối lượng khí không thay đổi, áp suất tăng lên gấp hai lần thì nhiệt độ tuyệt đối.
- A
- B
- C
- D
Do đây là quá trình đẳng tích nên PT=const , do đó khi tăng áp suất lên hai lần thì nhiệt độ cũng tăng lên hai lần.
Câu 7: Trong quá trình biến đổi đẳng tích của một lượng khí, khi nhiệt độ giảm thì
- A
- B
- C
- D
Với lượng khí nhất định, thể tích không đổi thì mật độ phân tử của chất khí không đổi.
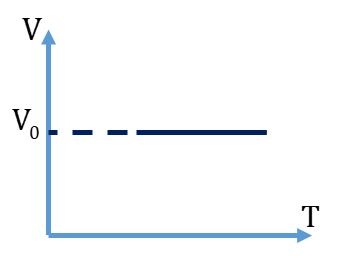
Câu 8: Trên đồ thị (V,T), đường đẳng tích là đường:
- A
- B
- C
- D
Trên đồ thị (V,T), đường đẳng tích là đường thẳng vuông góc với trục V, để thể hiện được thể tích là không đổi.

Câu 9: Quá trình nào sau đây được giải thích nhờ định luật Sác – lơ?
- A
- B
- C
- D
Định luật Sác – lơ là định luật cho quá trình đẳng tích, dễ nhận thấy chỉ có một đáp án thể hiện quá trình đẳng tích là đun nóng khí trong một bình kín.
Câu 10: Quá trình nào sau đây không phải là quá trình đẳng tích:
- A
- B
- C
- D
Bọt khí nổi lên từ đáy một hồ nước thì thể tích sẽ thay đổi, do thay đổi với áp suất bên ngoài khiến thể tích bong bóng sẽ càng ngày càng lớn khi nổi lên từ đáy.
Câu 11: Hệ thức nào sau đây phù hợp với định luật Sác – lơ?
- A
- B
- C
- D
Do đây là quá trình đẳng tích nên PT=const ,
Câu 12: Trong hệ toạ độ (p,T) đường biểu diễn nào sau đây là đường đẳng tích?
- A
- B
- C
- D
Do đây là quá trình đẳng tích nên PT=const , nên trong hệ trục tọa độ (p,T) thì đồ thị phải có dạng đường thẳng đi qua gốc của hệ trục tọa độ
Câu 13: Một lượng khí lí tưởng có nhiệt độ ban đầu là 300C biến đổi đẳng tích. Khi áp suất của khí tăng 2 lần thì nhiệt độ của khí là
- A
- B
- C
- D
Do đây là quá trình đẳng tích nên PT=const , do đó khi tăng áp suất lên hai lần thì nhiệt độ cũng tăng lên hai lần.
T2=2.T1=2.(273+30)=6060K⇒t2=3330C
Câu 14: Áp suất khí trơ trong bóng đèn tăng bao nhiêu lần khi đèn sáng nếu nhiệt độ đèn khi tắt là 250C , khi sáng là 3230C .
- A
- B
- C
- D
Áp dụng công thức:
p2p1=T2T1=323+27325+273=2
Câu 15: Trong quá trình biến đổi đẳng tích của một lượng khí, khi nhiệt độ tăng thì
- A
- B
- C
- D
Với lượng khí nhất định, thể tích không đổi thì mật độ phân tử của chất khí không đổi, hay khối lượng riêng của nó không thay đổi.
Câu 16: Trong hình bên là đường đẳng tích của hai lượng khí giống nhau kết quả nào sau đây là đúng khi so sánh các thể tích V1 và V2 ?


- A
- B
- C
- D
Kết quả V1<V2 là đúng.
Ứng với các thể tích khác nhau của cùng một lượng khí ta có những đường đẳng tích khác nhau. Đường ở trên ứng với thể tích nhỏ hơn.
Câu 17: Trong hệ tọa độ (p,T) đường biểu diễn nào là đường đẳng tích?
- A
- B
- C
- D
Do đây là quá trình đẳng tích nên PT=const , nên trong hệ trục tọa độ (p,T) thì đồ thị phải có dạng đường thẳng đi qua gốc của hệ trục tọa độ
Câu 18: Bơm không khí vào một cái bình cứng, nhiệt độ của không khí trong bình là 200C . Nếu nung nóng bình để nhiệt độ của không khí trong bình là 470C thì áp suất trong bình tăng lên bao nhiêu phần trăm? Bình không dãn nở.
- A
- B
- C
- D
Áp dụng công thức cho quá trình đẳng tích:
p1T1=p2T2⇒p2=p1T2T1Δp=p2−p1=p1(T2T1−1)⇒Δpp1=T2T1−1=47+27320+273−1=0,092=9,20/0