Ứng dụng thực tế của tam giác đồng dạng
Lý thuyết về Ứng dụng thực tế của tam giác đồng dạng
* Ứng dụng thực tế của tam giác đồng dạng:
- Đo gián tiếp chiều cao của vật
-Đo khoảng cách giữa hai địa điểm trong đó có một địa điểm không thể tới được.
Bài tập tự luyện có đáp án
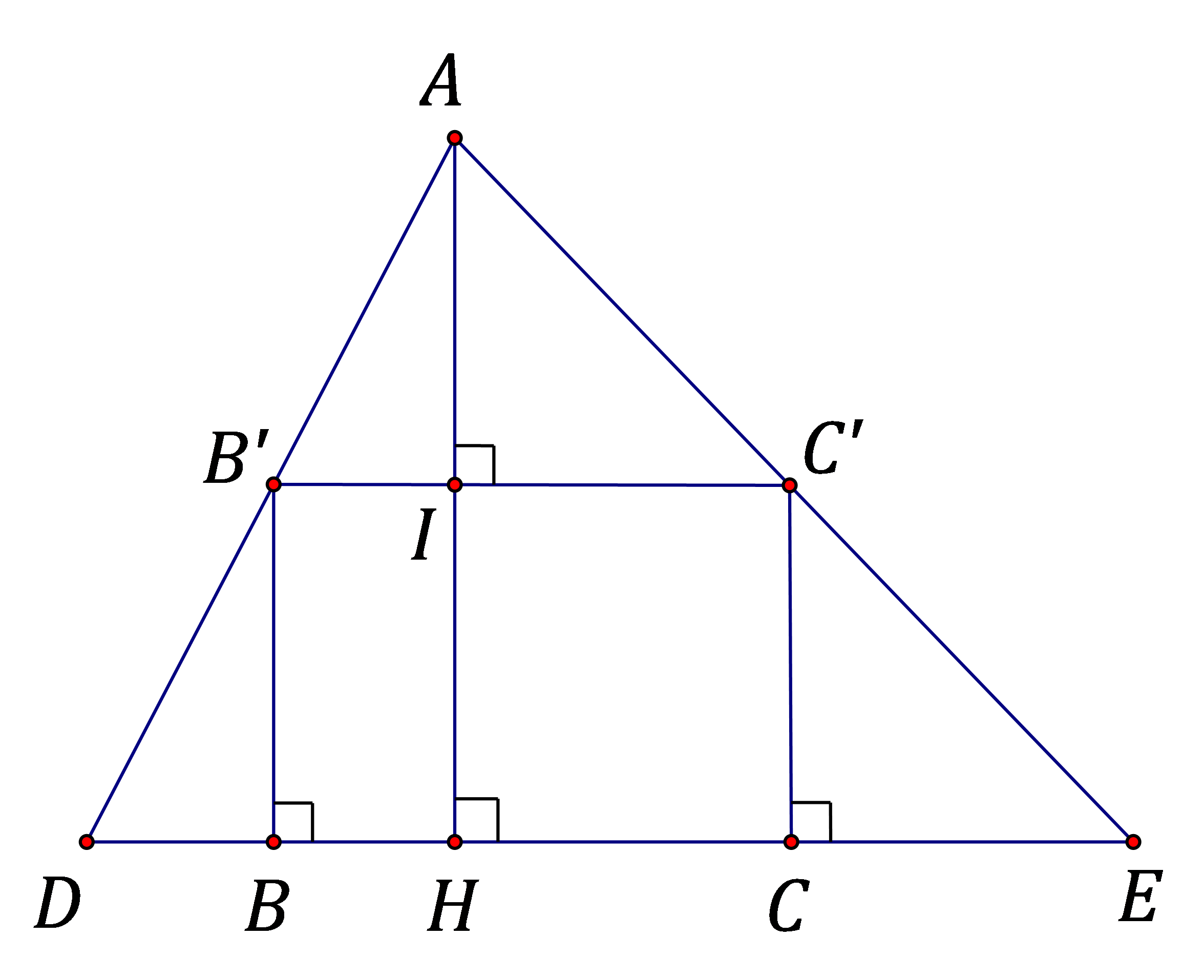
Câu 1: Một ngọn đèn đặt trên cao ở vị trí A, hình chiếu vuông góc của nó trên mặt đất là H. Người ta đặt một chiếc cọc dài 1,6m thẳng đứng ở hai vị trí B,C thẳng hàng với H, khi đó bóng của chiếc cọc dài 0,4m và 0,6m . Biết BC=1,4m , độ cao AH bằng


- A
- B
- C
- D

Gọi BD,CE là bóng của cọc và B′,C′ là vị trí tương ứng của đỉnh cọc.
Ta có BB′=CC′=1,6m,BD=0,4m,CE=0,6m , BC=1,4m . Đặt AH=x(m) .
Gọi I là giao điểm AH∩B′C′
ΔAB′C′ và ΔADE đồng dạng.
⇒AIAH=B′C′DE⇒AH−AIAH=DE−B′C′DE⇔IHAH=BD+CEDE⇒AH=IH.DEBD+CE=1,6.(0,4+1,4+0,6)0,4+0,6=3,84(m)
Câu 2: Một người đo chiều cao của một cây nhờ một cọc chôn xuống đất, cọc cao 2m và đặt xa cây 15m. Sau khi người ấy lùi xa cách cọc 0,8m thì nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng. Biết rằng khoảng cách từ chân đến mắt người ấy là 1,6m, chiều cao của cây là
- A
- B
- C
- D
Ta có hình vẽ như sau.

AB là vị trí đứng của người, M là vị trí mắt người. CD là vị trí đặt cọc, EF là vị trí của cây.
Khi đó ta có MB=1,6m , CD=2m , CB=0,8m , EC=15m .
Gọi EM∩CD=I
ΔEIC và ΔEMB đồng dạng
⇒ECEB=ICMB⇒IC=EC.MBEB=15.1,615+0,8=12079
⇒ID=DC−IC=2−12079=3879
EIEM=ECEB=1515+0,8=7579⇒IMEM=479
ΔMID và ΔMEF đồng dạng
⇒MIME=IDEF⇒EF=ID.MEMI=3879.794=192=9,5(m)
Vậy cây cao 9,5(m)
Câu 3: Một người đứng cách một ngôi nhà 200m, đặt 1 que dài 5cm, cách mắt 40cm theo phương thẳng đứng thì vừa vặn che lấp chiều cao của ngôi nhà. Chiều cao của ngôi nhà là
- A
- B
- C
- D
Ta có hình vẽ. A là vị trí đặt mắt, DE là chiều cao ngôi nhà, BC là độ dài bút, AH và AK lần lượt là khoảng cách của người đến bút và nhà, BC//DE .

Khi đó AK=200(m) , BC=5cm=0,05m,AH=40cm=0,4m
Ta có hai tam giác ABC và ADE đồng dạng ⇒AHAK=BCDE⇒DE=AK.BCAH=200.0,050,4=25(m)
Vậy nhà cao 25(m)
Câu 4: Để do khoẳng cách giữa 2 địa điểm A và B, trong đó B không tới được, người ta tiến hành đo và tính khoảng cách AB như hình sau. AB//DF , AD=15m , DC=10m , DF=8m . Khoảng cách AB bằng


- A
- B
- C
- D

Ta có ΔCDF và ΔCAB đồng dạng
⇒CDCA=DFAB⇒AB=CA.DFCD=(15+10).810=20(m)
Câu 5: Một giếng nước có đường kính DE=0,8m . Để xác định độ sâu BD của giếng, người ta đặt một chiếc gậy ở vị trí AC, A chạm miếng giếng, AC nhìn thẳng tới vị trí E ở góc của đáy giếng. Biết AB=0,9m , BC=0,2m . Độ sâu BD của giếng bằng


- A
- B
- C
- D

Hai tam giác ΔABC và ΔADE đồng dạng
ABAD=BCDE⇒ABAD−AB=BCDE−BC⇒ABBD=BCDE−BC⇒BD=AB.(DE−BC)BC=0,9.(0,8−0,2)0,2=2,7m
Câu 6: Bóng của tòa nhà Keangnam trên mặt đất dài 33,6m. Cùng thời điểm đó người ta quan sất thấy một thanh sắt cắm thẳng đứng trên mặt đất cam 2m có bóng dài 20cm. Chiều cao tòa nhà Keangnam là
- A
- B
- C
- D

BC là chiều cao tòa nhà Keangnam. AB là bóng của tòa nhà
B’C’ là chiều cao cọc sắt, A’B’ là bóng của cọc
Ta có ΔABC và ΔA′B′C′ đồng dạng
⇒A′B′AB=B′C′BC⇒BC=AB.B′C′A′B′=336m