Hình phẳng giới hạn bởi một đường cong và trục hoành
Lý thuyết về Hình phẳng giới hạn bởi một đường cong và trục hoành
Nếu hàm số y=f(x)y=f(x) liên tục trên đoạn [a;b][a;b] thì diện tích SS của hình phẳng giới hạn bởi đồ thị hàm số y=f(x)y=f(x), trục hoành và hai đường thẳng x=a,x=bx=a,x=b là S=b∫a|f(x)|dxS=b∫a|f(x)|dx
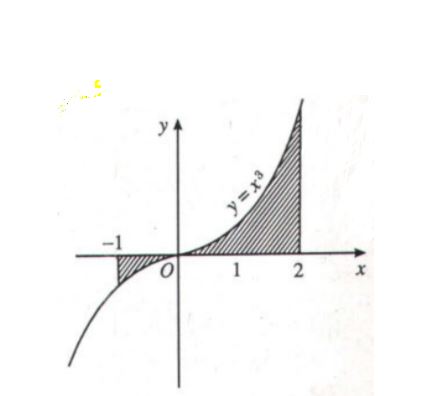
Ví dụ. Tính diện tích hình phẳng được giới hạn bởi đồ thị của hàm số y=x3y=x3, trục hoành và hai đường thẳng x=−1,x=2x=−1,x=2.
Giải. Ta có x3≤0x3≤0 trên đoạn [−1;0][−1;0] và x3≥0x3≥0 trên đoạn [0;2][0;2]. Áp dụng công thức tính diện tích ta có S=2∫−1|x3|dx=0∫−1(−x3)dx+2∫0x3dx=(−x44)|0−1+x44|20=174S=2∫−1∣∣x3∣∣dx=0∫−1(−x3)dx+2∫0x3dx=(−x44)∣∣∣0−1+x44∣∣∣20=174.
Bài tập tự luyện có đáp án
Câu 1: Diện tích hình thang cong T (hình bên) được tính theo công thức nào sau đây:


- A
- B
- C
- D
Do phần hình thang cong nằm toàn bộ phía trên trục hoành
⇒ST=b∫af(x)dx⇒ST=b∫af(x)dx
Chú ý nêú phần diện tích hình thang nằm phía dưới Ox thì
⇒ST=b∫a|f(x)|dx⇒ST=b∫a|f(x)|dx
Câu 2: Cho hàm số y=f(x)y=f(x) liên tục trên R, có đồ thì cắt trục hoành tại hai điểm phân biệt O(0;0),B(2;0). Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x) và trục hoành là
- A
- B
- C
- D
Ta có phương trình hoành độ giao điểm là f(x)=0⇔[x=0x=2
⇒S=2∫0|f(x)|dx
Câu 3: Cho hình vẽ
 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng?
 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng?- A
- B
- C
- D
Dựa vào diện tích các miền giới hạn bởi đường cong y=f(x) để đưa ra được so sánh đúng là a∫0f(x)dx<c∫bf(x)dx