Định nghĩa hai vectơ cùng phương, cùng hướng
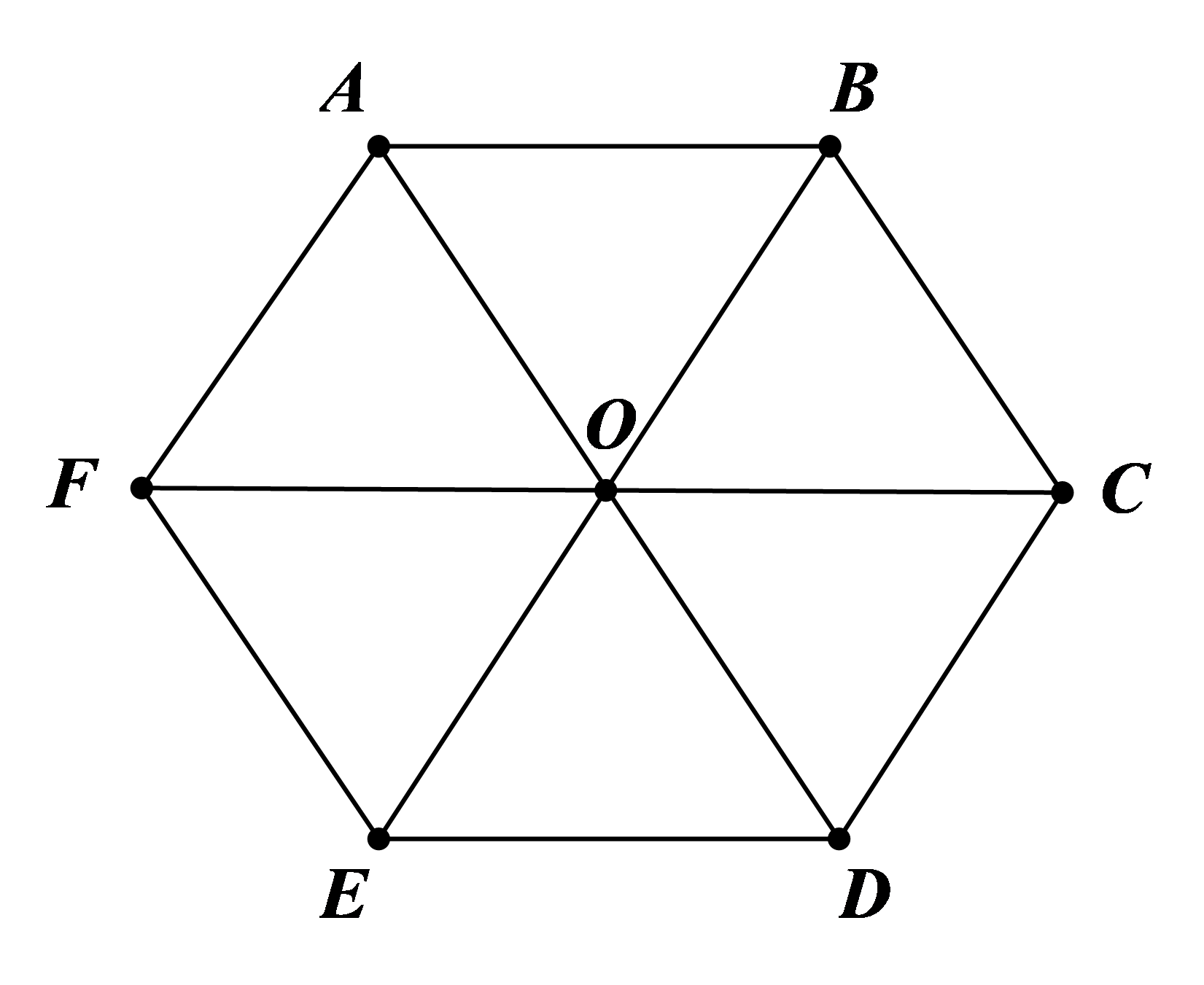
Lý thuyết về Định nghĩa hai vectơ cùng phương, cùng hướng
Hai vectơ cùng phương, cùng hướng
- Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau
Rõ ràng vectơ-không cùng phương với mọi vectơ.
- Nếu hai vectơ cùng phương thì hoặc chúng cùng hướng hoặc chúng ngược hướng
Chú ý: Ta quy ước rằng vectơ-không cùng hướng với mọi vectơ
Bài tập tự luyện có đáp án
Câu 1: Cho lục giác đều ABCDEFABCDEF tâm O . Số các vectơ khác →0 cùng phương với →OC có điểm đầu và cuối là đỉnh của lục giác là
- A
- B
- C
- D
Các vecto thỏa mãn đề bài lần lượt là →AB,→BA,→ED,→DE,→FC,→CF.
Câu 2: Trên đường thẳng MN lấy điểm P sao cho →MN=−3→MP . Hình vẽ nào sau đây xác định đúng vị trí điểm P ?
- A
- B
- C
- D
→MN=−3→MP . Vì −3<0 nên →MN,→MP ngược hướng
⇒M nằm giữa N,P và MN=3MP
Câu 3: Cho tam giác ABC đều cạnh a . Khẳng định nào sau đây đúng?
- A
- B
- C
- D
Vì tam giác ABC đều cạnh a nên |→AB|=AB=a .
Câu 4: Cho ba điểm M,N,P thẳng hàng, trong đó điểm N nằm giữa hai điểm M và P Khi đó các cặp vectơ nào sau đây cùng hướng?
- A
- B
- C
- D
Ta có N nằm giữa hai điểm M và P nên →MN và →MP cùng hướng
Câu 5: Cho tứ giác ABCD. Số các vectơ khác →0 có điểm đầu và cuối là đỉnh của tứ giác bằng:
- A
- B
- C
- D
Các vecto lần lượt là: →AB,→BA,→AC,→CA,→BC,→CB,→AD,→DA,→DC,→CD,→BD,→DB
Câu 6: Cho →AB ≠ →0 và một điểm C, có bao nhiêu điểm D thỏa mãn: |→AB|=|→CD|
- A
- B
- C
- D
Các điểm D thỏa mãn đề bài nằm trên đường tròn tâm C bán kính AB.
Câu 7: Chọn khẳng định đúng.
- A
- B
- C
- D
Theo định nghĩa hai vectơ bằng nhau trong SGK: Hai vectơ bằng nhau là hai vectơ cùng hướng và cùng độ dài.
Câu 8: Cho lục giác đều ABCDEF tâm O . Số các vectơ bằng →OC có điểm đầu và cuối là đỉnh của lục giác là
- A
- B
- C
- D

Các vecto thỏa mãn đề bài lần lượt là →AB,→ED.
Câu 9: Cho tam giác ABC có thể xác định bao nhiêu vectơ khác vectơ →0 có điểm đầu và điểm cuối là đỉnh A,B,C ?
- A
- B
- C
- D
Các vecto lần lượt là →AB,→BA,→AC,→CA,→BC,→CB.
Câu 10: Từ hai điểm A,B phân biệt xác định được bao nhiêu vectơ khác →0 ?
- A
- B
- C
- D
Từ hai điểm A,B phân biệt có hai vectơ khác →0 là →AB và →BA .
Câu 11: Cho tam giác ABC.E,F lần lượt là trung điểm của AB,AC. Gọi B′,C′ lần lượt là điểm đối xứng của B qua F và của C qua E. Khẳng định nào sau đây là sai?
- A
- B
- C
- D

Vì F là trung điểm của AC,BB′ nên ABCB′ là hình bình hành ⇒AB′//BC
Tương tự ta co AC′BC cũng là hình bình hành ⇒AC′//BC
⇒C′,A,B′ thẳng hàng
ΔABC có FE là đường trung bình
Suy ra: B′C′//FE//BC
Mà: {BC=2EFBC=AC′=AB′B′C′=AB′+AC′⇒B′C′=4EF
Câu 12: Cho hai vec tơ →a và →b không cùng phương và hai vectơ →u=→a+2→b , →v=−3→a+(2x−1)→b . Tìm giá trị của x để →u,→v cùng phương?
- A
- B
- C
- D
Vì hai vectơ →u,→v cùng phương nên:
−3→a+(2x−1)→b=k(→a+2→b)
⇔(k+3)→a+(2k−2x+1)→b=→0⇔{k+3=02k−2x+1=0⇔{k=−3x=−52
Câu 13: Cho tứ giác ABCD nội tiếp (O).B′,D′ lần lượt là điểm đối xứng của B,D qua O . H là trực tâm tam giác BCD . Trong các cặp vecto →BD và →D′B′ ; →CD′ và →HB ; →D′B và →CH ; →DH và →B′C có bao nhiêu cặp vecto cùng hướng
- A
- B
- C
- D

Ta có tam giác DD′C vuông tại C⇒D′C⊥DC
H là trực tâm tam giác BDC⇒BH⊥DC
⇒D′C//BH
Tương tự ta có CH//BD′
⇒BD′CH là hình bình hành
Tương tự DHCB′ cũng là hình bình hành
⇒→DH=−→CB′
Câu 14: Cho hình bình hành ABCD . Hai điểm M,N lần lượt là trung điểm DC,AB. Điểm I là giao điểm của AM và DN , K là giao điểm của BM và CN . Khi đó vecto cùng hướng với →NI là:
- A
- B
- C
- D

ABCD là hình bình hành ⇒AB=CD
Vì M, N lần lượt là trung điểm của CD, AB mà AB = CD nên BN=CM(=AB2=DC2)
ABCD là hình bình hành ⇒AB//CD⇒BN//CM
Vậy BCMN là hình bình hành ⇒ K là trung điểm BM.
Xét tam giác ABM có N,K lần lượt là trung điểm của AB,BM⇒NK là đường trung bình của tam giác ABM⇒NK//AB//IM
Tương tự ta có NI//MK
⇒ Tứ giác IMKN là hình bình hành
⇒→NI=→KM
Mà →BK=→KM
⇒→NI=→BK
⇒ →BK,→NI cùng hướng
Câu 15: Cho điểm N thuộc đoạn OM sao cho OM=kON . Vẽ đường tròn (O,ON) . Từ M kẻ hai tiếp tuyến đến (O) tiếp xúc với (O) lần lượt tại A,B . Tìm giá trị của k để →AN cùng phương với →BO
- A
- B
- C
- D

→AN cùng phươngvới →BO ⇔AN//BO
Ta có MA=MB (Tính chất tiếp tuyến)
⇒ΔAOM=ΔBOM⇒^AON=^BON
⇒ΔAON=ΔBON (c−g−c) ⇒^OAN=^OBN
Mà ^OBN+^ANB=1800 (Vì AN//BO ) ⇒^ANB+^OAN=1800
⇒ BN//OA
⇒OANB là hình bình hành ⇒AN=OB
Mà OB=OA=ON ⇒ AN=OA=ON⇒ và ΔOAN đều ⇒^AON=60∘
Lại có ΔOAM vuông tại A ⇒OM=2OA=2ON
⇒k=2
Câu 16: Cho hình thang ABCD có AB//CD và CD=3AB . O là giao điểm hai đường chéo của hình thang. Trên OC,OD lần lượt lấy hai điểm I,J sao cho OIIC=OJJD=k . Tìm giá trị của k để →AJ và →BI cùng hướng?
- A
- B
- C
- D

Theo giả thiết: OIIC=OJJD=1k⇒JI//DC//AB
→AJ và →BI cùng hướng ⇒AJ//BI
⇒ABIJ là hình bình hành ⇒AB=JI
Mà: CD=3AB⇒CD=3JI
⇒OIIC=OJJD=12
Câu 17: Cho hình thang ABCD với CD là đáy lớn. Kẻ BE//AD
(E∈DC) . F là trung điểm của cạnh BC và H là trung điểm của đoạn EC . Cặp vecto không cùng phương là:
- A
- B
- C
- D

Tam giác BEC có F là trung điểm BC và H là trung điểm của EC
⇒FH là đường trung bình của tam giác BCE
⇒FH//BE//AD
Hay các vecto →AD,→BE,→FH cùng phương
Ta có AB≠EH⇒ABHE không là hình bình hành
Khi đó →AE,→BH không cùng phương với nhau
Câu 18: Biết rằng hai vectơ →a và →b không cùng phương nhưng hai vectơ 7→a+3→b và −72→a+(2−x)→b cùng phương. Khi đó giá trị của x là:
- A
- B
- C
- D
Vì hai vectơ 7→a+3→b và −72→a+(2−x)→b cùng phương nên:
−72→a+(2−x)→b=k(7→a+3→b)
⇔(7k+72)→a+(3k+x−2)→b=→0⇔{7k+72=03k+x−2=0⇔{k=−12x=72
Câu 19: Cho tam giác ABC.E,F lần lượt là trung điểm của AB,AC. Gọi B′,C′ lần lượt là điểm đối xứng của B qua F và của C qua E. Số cặp vecto →FE và →B′A ; →FE và →B′C′ ; →C′B′ và →BC ; →FE và →BC cùng hướng là
- A
- B
- C
- D

ΔABCcó FE là đường trung bình
⇒FE//BC và →FE,→BC không cùng hướng
Ta có C′ACB,AB′CB đều là 2 hình bình hành nên
C′,A,B′ thẳng hàng ⇒C′B′//BC
Khi đó cả 3 cặp đề bài cho đều cùng hướng với nhau
Câu 20: Cho tam giác ABC có trực tâm H và O là tâm đường tròn ngoại tiếp. Gọi B′ là điểm đối xứng của B qua O . Cặp vecto cùng hướng là:
- A
- B
- C
- D

Vì H là trực tâm ΔABC⇒ CH⊥AB
Có: ΔBAB′ vuông tại A⇒B′A⊥AB
Suy ra: AB′//CH
Mà lại có: {AH⊥BCB′C⊥BC⇒AH//B′C
Từ đó ta có: AHCB′ là hình bình hành ⇒→AH=→B′C hay →AH và →B′C cùng hướng
Câu 21: Cho tam giác ABC . Trên cạnh AC lấy điểm E sao cho AC=3AE. Kẻ EF//AB . Trên đoạn AB lấy điểm I sao cho AI=2IB . Khi đó khẳng định nào sau đây là đúng?
- A
- B
- C
- D

Ta có EF//AB⇒AI và EF cùng phương
Theo giả thiết: AI=2IB⇒AIAB=23
Mà: FCBC=CEAC=23
⇒IF//AC
⇒ AEFI là hình bình hành.
Câu 22: Biết rằng hai vectơ →a và →b không cùng phương nhưng hai vectơ →a+3→b và x→a+(x2−4)→b cùng hướng. Khi đó giá trị của x là:
- A
- B
- C
- D
Vì hai vectơ →a+3→b và x→a+(x2−4)→b cùng phương nên:
x→a+(x2−4)→b=k(→a+3→b)
⇔(k−x)→a+(3k−x2+4)→b=→0⇔{k−x=03k−x2+4=0⇔{x=kx2−3x−4=0⇔[x=k=−1x=k=4
Mặt khác 2 vecto đã cho cùng hướng nên x>0⇒x=4
Câu 23: Cho N là trung điểm của đoạn OM . Vẽ đường tròn (O,ON) . Từ M kẻ hai tiếp tuyến đến (O) tiếp xúc với (O) lần lượt tại A,B . Chọn khẳng định sai:
- A
- B
- C
- D

+ ΔOAM vuông tại A có AN là trung tuyến ⇒ON=AN=NM
+ OA=ON⇒OA=AN
+ Tương tự với ΔOBN ta có OB=BN
+ OA=OB⇒OA=OB=AN=BN
+ Suy ra: OANB là hình thoi ⇒ →OA=−→NB
Khi đó có OA=ON=NA⇒ΔONA là tam giác đều ⇒^ANO=600
Tương tự có ^BNO=600⇒^ANB=1200
Câu 24: Cho tam giác đều ABC nội tiếp đường tròn (O) . D là điểm đối xứng của B qua O . Khi đó,
- A
- B
- C
- D

Tam giác ABC đều ⇒O là trực tâm tam giác ABC.
⇒CO⊥AB
Mà DA⊥AB⇒CO//DA
Chứng minh tương tự ta có AO//DC.
⇒AOCD là hình bình hành.
⇒→AO,→CD ngược hướng.
Câu 25: Biết rằng hai vec tơ →a và →b không cùng phương nhưng hai vec tơ 2→a−6→b và →a+(x2+x−9)→b cùng phương. Khi đó giá trị của x>0 là:
- A
- B
- C
- D
Vì hai vectơ 2→a−6→b và →a+(x2+x−9)→b cùng nên:
→a+(x2+x−9)→b=k(2→a−6→b)
⇔(2k−1)→a+(−x2−x−6k+9)→b=→0⇔{2k−1=0x2+x+6k−9=0⇔{k=12[x=2>0x=−3
Xem thêm các bài tiếp theo bên dưới