Các trường hợp bằng nhau của tam giác vuông
Lý thuyết về Các trường hợp bằng nhau của tam giác vuông
– Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (theo trường hợp c.g.c)
– Nếu một cạnh của tam giác vuông này và một góc nhọn kề cạnh ấy bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
– Nếu cạnh huyền và môt cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
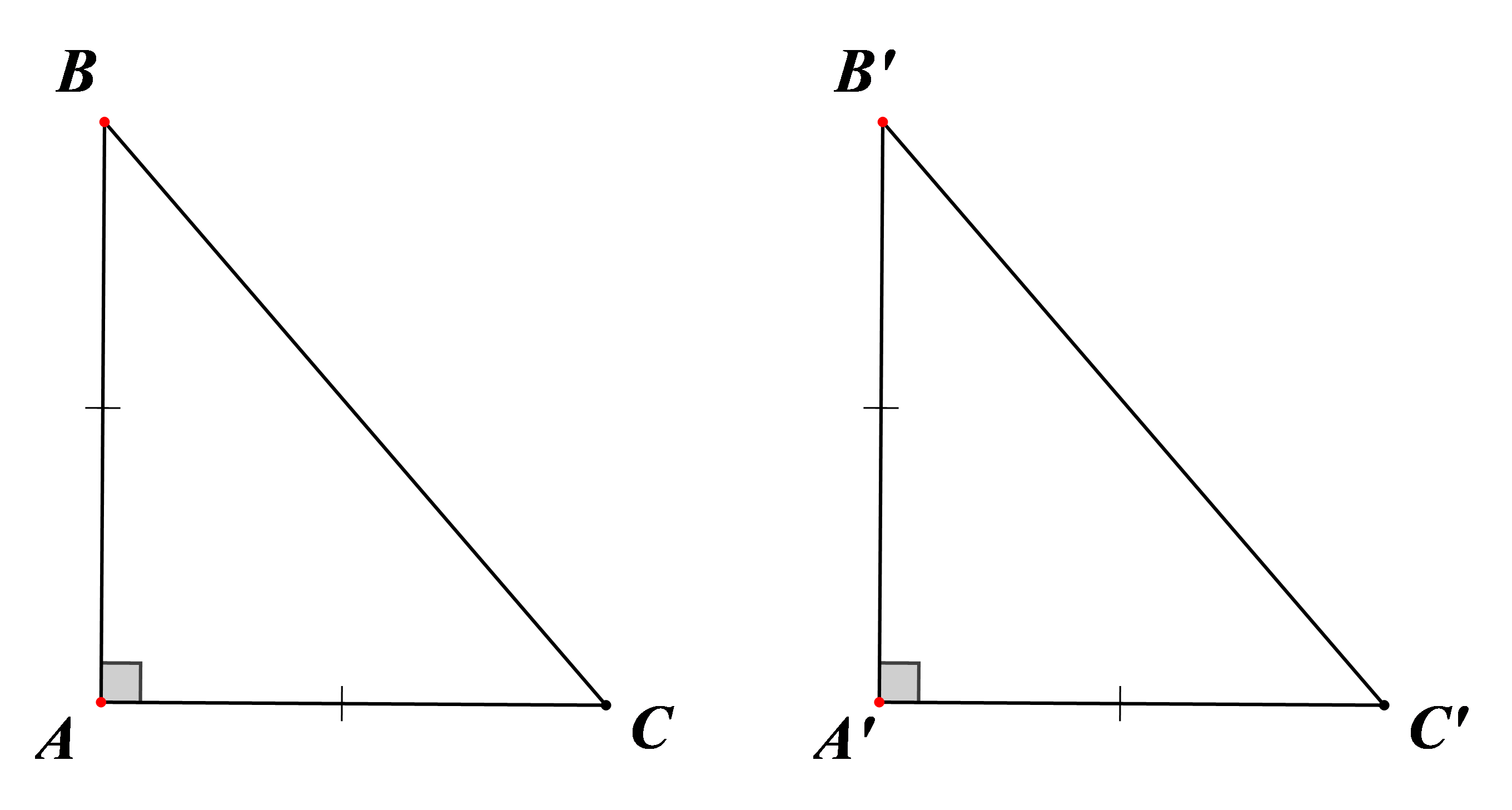
Hai tam giác \[\Delta ABC = \Delta A'B'C'\]
– Nếu \[AB = A'B';AC = A'C'\]
– Nếu \[AB = A'B';\widehat B = \widehat {B'}\] hoặc \[AC = A'C';\widehat B = \widehat {B'}\]
– Nếu \[AB = A'B';BC=B'C'\] hoặc \[AC = A'C';BC=B'C'\]
Bài tập tự luyện có đáp án
Câu 1: Cho hình vẽ bên 
Số đo góc NQM là
Số đo góc NQM là
- A
- B
- C
- D
Xét $ \Delta MNP $ và $ \Delta NMQ $ có
$ \left\{ \begin{array}{l} \widehat{NMP}=\widehat{MNQ}={{90}^{o}} \\ MN\,\,\,chung \\ NP=MQ \end{array} \right.\Rightarrow \Delta MNP=\Delta NMQ $ (cạnh huyền-cạnh góc vuông) $ \Rightarrow \widehat{NQM}=\widehat{MPN}={{48}^{o}} $
Câu 2: Cho tam giác ABC. Các tia phân giác của góc B và C cắt nhau ở I. Kẻ $ ID\bot AB\left( D\in AB \right), $ kẻ $ IE\bot AC\left( E\in AC \right). $
Khẳng định nào sau đây là sai?
- A
- B
- C
- D

Kẻ $ IH\bot BC\,\,(H\in \,BC) $ .
$ \Delta BID=\Delta BIH $ (cạnh huyền-góc nhọn) $ \Rightarrow ID=IH. $ (1)
$ \Delta CIE=\Delta CIH $ (cạnh huyền-góc nhọn) $ \Rightarrow IE=IH. $ (2)
Từ (1) và (2) $ \Rightarrow ID=IE $ .
Khi đó: $ \Delta IAD=\Delta IAE $ (cạnh huyền-cạnh góc vuông) $ \Rightarrow AD=AE\,;\,\widehat{DAI}=\widehat{EAI} $ .
Ta có: $ \,\widehat{DAI}=\widehat{EAI}\Rightarrow $ AI là tia phân giác của $ \widehat{BAC} $ .
Vậy khẳng định sai cần chọn là: " $ \Delta IAD=\Delta IEA $ " (Do viết sai thứ tự đỉnh tương ứng).
Câu 3: Cho hình vẽ.
 Hình vẽ trên có bao nhiêu cặp tam giác vuông bằng nhau?
Hình vẽ trên có bao nhiêu cặp tam giác vuông bằng nhau?
 Hình vẽ trên có bao nhiêu cặp tam giác vuông bằng nhau?
Hình vẽ trên có bao nhiêu cặp tam giác vuông bằng nhau?- A
- B
- C
- D
$ \Delta ADE $ cân tại A (Vì $ AD=AE $ ) $\,\, \Rightarrow \widehat {{D_1}} = \widehat {{E_1}} \Rightarrow \widehat {ADB} = \widehat {AEC}.$
Xét $ \Delta ADB $ và $ \Delta AEC $ có: $ AD=AE;\,\widehat{ADB}=\widehat{AEC}\,;\,BD=EC $
$ \Rightarrow $ $ \Delta ADB=\Delta AEC\left( c.g.c \right)\Rightarrow {{\widehat{A}}_{1}}={{\widehat{A}}_{2}}. $
Khi đó: $ \Delta AHD=\Delta AKE $ (cạnh huyền-góc nhọn) $ \Rightarrow DH=EK. $
$ \Delta DHB=\Delta EKC $ (cạnh huyền-cạnh góc vuông).
Vậy có 2 cặp tam giác vuông bằng nhau.
Câu 4: Cho hình vẽ. 
Khẳng định nào sau đây là đúng?

Khẳng định nào sau đây là đúng?
- A
- B
- C
- D
Xét tam giác OBK và tam giác OAK có:
$ \widehat{OBK}=\widehat{OAK}={{90}^{o}}\,;\,OB=OA $ ; cạnh $ OK $ chung
$ \Rightarrow $ $ \Delta OBK=\Delta OAK $ (cạnh huyền-góc vuông)
$ \Rightarrow {{\widehat{O}}_{1}}={{\widehat{O}}_{2}}\Rightarrow $ OK là tia phân giác của góc $ \widehat{BOA} $ .
Vậy khẳng định đúng cần chọn là: "OK là tia phân giác của $ \widehat{BOA} $ ".
Câu 5: Cho tam giác ABC vuông tại C, có $ \widehat{BAC}={{60}^{o}} $ . Tia phân giác của $ \widehat{BAC} $ cắt BC ở E. Kẻ $ EK\bot AB(K\in AB), $ kẻ $ BD\bot AE(D\in AE) $ . Tam giác BDK là tam giác gì?
- A
- B
- C
- D
Xét $ \Delta DBE $ và $ \Delta KBE $ có $ \left\{ \begin{array}{l} BE\,\,chung \\ \widehat{DBE}=\widehat{KBE}={{30}^{o}} \\ \widehat{B\text{D}E}=\widehat{BKE}={{90}^{o}} \end{array} \right.\Rightarrow \Delta DBE=\Delta KBE $ (cạnh huyền – góc nhọn)
$ \left\{ \begin{array}{l} BD=BK \\ \widehat{DBE}=\widehat{EBK}={{30}^{o}}\Rightarrow \widehat{DBK}={{60}^{o}} \end{array} \right.\Rightarrow \Delta B\text{D}K $ đều.
Câu 6: Cho tam giác ABC có M là trung điểm của BC. Từ B và C kẻ các đường thẳng BE và CF cùng vuông góc với đường thẳng AM (E, F thuộc đường thẳng AM).
Chọn khẳng định sai.
- A
- B
- C
- D

Xét $ \Delta BEM $ và $ \Delta CFM $ có:
$ \widehat{BEM}=\widehat{CFM}={{90}^{o}} $ ;
$ {{\widehat{M}}_{1}}={{\widehat{M}}_{2}} $ (đối đỉnh), $ MB=MC $ (Vì M là trung điểm của BC)
$ \Rightarrow \Delta BEM=\Delta CFM $ (cạnh huyền – góc nhọn).
$ \Rightarrow ME=MF;BE=CF. $
Vì $ BE\bot AM,CF\bot AM\Rightarrow BE//CF. $
Vậy khẳng định sai cần chọn là: " $ \Delta BME=\Delta CFM $ " (Do viết không đúng thứ tự đỉnh tương ứng).
Câu 7: Cho góc xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B. Gọi M là trung điểm của đoạn thẳng AB. Vẽ tia OM.
Từ A và B hạ các đường AE và BF cùng vuông góc với tia OM (E, F thuộc tia OM)
Khẳng định nào sau đây là sai ?
- A
- B
- C
- D

Xét $ \Delta AME $ và $ \Delta BMF $ có:
$ \widehat{AEM}=\widehat{BFM}={{90}^{o}} $ ;
$ MB=MA $ (Vì M là trung điểm của AB);
$ \widehat{AME}=\widehat{BMF} $ (đối đỉnh)
$ \Rightarrow \Delta MAE=\Delta MBF $ (cạnh huyền – góc nhọn)
$ \Rightarrow AE=BF $ .
Vậy khẳng định sai cần chọn là: " $ \widehat{AME}=\widehat{BFM} $ ".
Câu 8: Chọn câu trả lời đúng nhất. Cho hình vẽ bên

$ \Delta ABC=\Delta DBC $ theo trường hợp nào?
Cho hình vẽ bên
$ \Delta ABC=\Delta DBC $ theo trường hợp nào?
- A
- B
- C
- D
Xét $ \Delta ABC $ và $ \Delta DBC $ có
$ \left\{ \begin{array}{l} \widehat{ACB}=\widehat{DCB}={{40}^{o}} \\ \widehat{BAC}=\widehat{B\text{D}C}={{90}^{o}} \\ BC\,\,\,chung \end{array} \right.\Rightarrow \Delta ABC=\Delta DBC $ (cạnh huyền - góc nhọn)
Câu 9: Cho tam giác ABC vuông tại C, có $ \widehat{BAC}={{60}^{o}} $ . Tia phân giác của $ \widehat{BAC} $ cắt BC ở E. Kẻ $ EK\bot AB(K\in AB), $ kẻ $ BD\bot AE(D\in AE) $ . Gọi F là giao điểm của BD và AC. Biết AB = 3 cm. Độ dài BF là
- A
- B
- C
- D
Xét $ \Delta DBE $ và $ \Delta KBE $ có $ \left\{ \begin{array}{l} BE\,\,chung \\ \widehat{DBE}=\widehat{KBE}={{30}^{o}} \\ \widehat{B\text{D}E}=\widehat{BKE}={{90}^{o}} \end{array} \right.\Rightarrow \Delta DBE=\Delta KBE $ (cạnh huyền – góc nhọn)
$ \widehat{DBE}=\widehat{EBK}={{30}^{o}}\Rightarrow \widehat{DBK}={{60}^{o}} $ mà $ \widehat{BAC}={{60}^{o}} $ nên $ \Delta ABF $ đều do đó BF=AB=3cm.
Câu 10: Cho tam giác ABC và DMN có $ \widehat{B}=\widehat{M}={{90}^{0}},\widehat{A}=\widehat{D}. $ Hãy bổ sung thêm một điều kiện bằng nhau để $ \Delta ABC=\Delta DMN. $ Khẳng định nào sau đây là sai?
- A
- B
- C
- D

Bổ sung $ AB=DM $ thì $ \Delta ABC=\Delta DMN $ (g.c.g).
Bổ sung $ BC=MN $ thì $ \Delta ABC=\Delta DMN $ (g.c.g) (vì $ \widehat{A}=\widehat{D}\,\Rightarrow $ $ \widehat{C}=\widehat{N} $ ).
Bổ sung $ AC=DN $ thì $ \Delta ABC=\Delta DMN $ (cạnh huyền-góc nhọn).
Vậy khẳng định sai cần chọn là: " $ AC=DM $ ".
Câu 11: Cho tam giác ABC cân tại C. Các đường trung trực của CA và của CB cắt nhau tại I. Gọi E, F lần lượt là trung điểm của CA, CB. Khi đó khẳng định nào sau đây là khẳng định sai.
- A
- B
- C
- D

Vì IE là đường trung trực của AC nên $ IE\bot AC $ và $ EA=EC=\dfrac{1}{2}AC $ . (1)
Vì IF là đường trung trực của BC nên $ IF\bot BC $ và $ CF=BF=\dfrac{1}{2}BC $ . (2)
Theo đề bài $ \Delta ABC $ cân tại C nên $ AC=BC $ . (3)
Từ (1) (2) và (3) suy ra $ EC=CF. $
Xét $ \Delta ICE $ và $ \Delta ICF $ có:
$ \widehat{CEI}=\widehat{CFI}={{90}^{o}} $ ; cạnh CI chung ; $ CE=CF $ (theo chứng minh trên)
$ \Rightarrow $ $ \Delta ICE=\Delta ICF $ (cạnh huyền-cạnh góc vuông)
$ \Rightarrow {{\widehat{C}}_{1}}={{\widehat{C}}_{2}}\,;\,\widehat{CIE}=\widehat{CIF}\,;\,\,IE=IF $
Ta có: $ {{\widehat{C}}_{1}}={{\widehat{C}}_{2}}\,\Rightarrow $ CI là tia phân giác của góc C.
Vậy khẳng định sai cần chọn là: " $ \Delta ICE=\Delta IFC $ ".(Do viết không đúng thứ tự đỉnh tương ứng).
Câu 12: Cho hai tam giác nhọn ABC và A’B’C’ có $ AB=A'B',AC=A'C',\widehat{B}=\widehat{B'}. $ Vẽ $ AH\bot BC $ tại H, $ A'H'\bot B'C' $ tại H’.
Chọn khẳng định sai.
- A
- B
- C
- D

$ \Delta HBA=\Delta H'B'A' $ (cạnh huyền-góc nhọn) $ \Rightarrow AH=A'H',BH=B'H'. $
$ \Delta HAC=\Delta H'A'C' $ (cạnh huyền-cạnh góc vuông) $ \Rightarrow HC=H'C'. $
Do $ BH+HC=B'H'+H'C'\Rightarrow BC=B'C'. $
Vậy khẳng định sai cần chọn là: $ \Delta HBA=\Delta H'A'B' $ (Do viết sai thứ tự đỉnh tương ứng).
Câu 13: Cho tam giác ABC cân tại B. Qua A kẻ đường vuông góc với AB, qua C kẻ đường vuông góc với CB, chúng cắt nhau tại K.
Chọn khẳng định sai.
- A
- B
- C
- D

Xét $ \Delta ABK $ và $ \Delta CBK $ có:
$ \widehat{BAK}=\widehat{BCK}={{90}^{o}}\,; $ $ BA=BC $ (Vì $ \Delta ABC $ cân tại B); Cạnh $ BK $ chung
$ \Rightarrow $ $ \Delta ABK=\Delta CBK $ (cạnh huyền-cạnh góc vuông)
$ \Rightarrow \,{{\widehat{B}}_{1}}={{\widehat{B}}_{2}}\,;\,\,\widehat{AKB}=\widehat{CKB} $
Ta có: $ {{\widehat{B}}_{1}}={{\widehat{B}}_{2}}\Rightarrow $ BK là tia phân giác của góc B.
Vậy khẳng định sai cần chọn là: " $ \widehat{BAK}=\widehat{BKC} $ ".
Câu 14: Cho góc xOy. Trên tia phân giác của góc đó lấy một điểm M, từ M hạ MB vuông góc với Ox (B thuộc tia Ox), MA vuông góc với Oy (A thuộc tia Oy).
Chọn khẳng định sai.
- A
- B
- C
- D

Xét $ \Delta MOB $ và $ \Delta MOA $ có:
$ \widehat{MBO}=\widehat{MAO}={{90}^{o}} $ ;
$ \widehat{MOB}=\widehat{MOA} $ (Vì OM là tia phân giác);
Cạnh OM chung
$ \Rightarrow $ $ \Delta MOB=\Delta MOA $ (cạnh huyền, góc nhọn).
$ \Rightarrow MA=MB\Rightarrow \Delta MAB $ cân tại M.
Vậy khẳng định sai cần chọn là: " $ \Delta MAB $ cân tại A"/
Xem thêm các bài tiếp theo bên dưới