Thời gian ngắn nhất
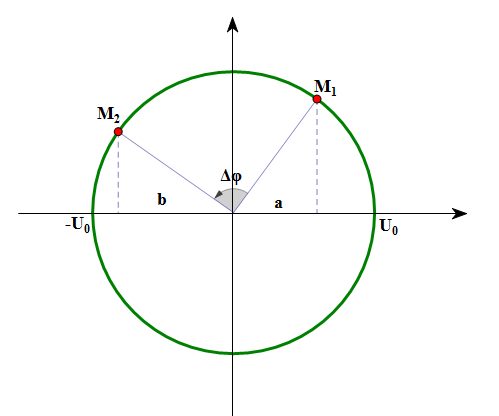
Lý thuyết về Thời gian ngắn nhất
Thời gian ngắn nhất đi từ ${{M}_{1}}\to {{M}_{2}}$
$\Delta \varphi =\omega .\Delta t\Leftrightarrow \Delta \varphi =\dfrac{2\pi }{T}.\Delta t$
Trong đó: $\Delta \varphi =\arcsin\dfrac{a}{{{U}_{0}}}+\arcsin \dfrac{b}{{{U}_{0}}}$
Thời gian ngắn nhất đi từ ${{N}_{1}}\to {{N}_{2}}$
$\Delta \varphi =\omega .\Delta t\Leftrightarrow \Delta \varphi =\dfrac{2\pi }{T}.\Delta t$
Trong đó: $\Delta \varphi =\arccos \dfrac{x}{{{U}_{0}}}+\arccos \dfrac{y}{{{U}_{0}}}$
Bài tập tự luyện có đáp án
Câu 1: Một mạch dao động lí tưởng đang có dao động điện từ tự do với chu kì dao động T. Tại thời điểm $ t=0 $ , điện tích trên một bản tụ điện đạt giá trị cực tiểu. Điện tích trên bản tụ này bằng 0 ở thời điểm đầu tiên (kể từ $ t=0 $ ) là
- A
- B
- C
- D

Dựa vào vòng tròn lượng giác ta có: $ \Delta \varphi =\dfrac{\pi }{2}\Rightarrow \Delta t=\dfrac{T}{4} $
Câu 2: Một mạch dao động điện từ LC lí tưởng gồm cuộn cảm thuần có độ tự cảm $ 0,25H $ và tụ điện có điện dung $ 1\mu F $ . Trong mạch có dao động điện từ tự do. Khoảng thời gian giữa hai lần liên tiếp mà điện tích trên một bản tụ điện có độ lớn bằng 0 là
- A
- B
- C
- D
$ T=2\pi \sqrt{LC}=\pi {{.10}^{-3}}s $
Khoảng thời gian giữa hai lần liên tiếp mà điện tích trên một bản tụ điện có độ lớn bằng 0 là: $ \dfrac{T}{2}=5\pi {{.10}^{-4}}s $Câu 3: Một mạch dao động điện từ LC lí tưởng gồm cuộn cảm thuần có độ tự cảm $ 25\mu H $ và tụ điện có điện dung $ 25\mu F $ . Trong mạch có dao động điện từ tự do. Khoảng thời gian giữa hai lần liên tiếp mà điện áp trên một bản tụ điện có độ lớn cực đại là
- A
- B
- C
- D
$ T=2\pi \sqrt{LC}=5\pi {{.10}^{-5}}s $
Khoảng thời gian giữa hai lần liên tiếp mà điện áp trên một bản tụ điện có độ lớn cực đại là: $ \dfrac{T}{2}=2,5\pi {{.10}^{-5}}s $
Câu 4: Một mạch dao động điện từ LC lí tưởng gồm cuộn cảm thuần có độ tự cảm $ 5\mu H $ và tụ điện có điện dung $ 5\mu F $ . Trong mạch có dao động điện từ tự do. Khoảng thời gian giữa hai lần liên tiếp mà điện tích trên một bản tụ điện có độ lớn cực đại là
- A
- B
- C
- D
$ T=2\pi \sqrt{LC}=\pi {{.10}^{-5}}s $
Khoảng thời gian giữa hai lần liên tiếp mà điện tích trên một bản tụ điện có độ lớn cực đại là: $ \dfrac{T}{2}=5\pi {{.10}^{-6}}s $Câu 5: Một mạch dao động điện từ lí tưởng đang có dao động điện từ tự do, với tần số góc $ \omega =25\pi {{.10}^{4}}rad/s $ . Thời điểm ban đầu điện tích trên tụ điện đạt giá trị cực đại. Thời gian ngắn nhất để tụ phóng hết điện tích là
- A
- B
- C
- D
$ T=\dfrac{2\pi }{\omega }=\dfrac{2\pi }{25\pi {{.10}^{4}}}={{8.10}^{-6}}s=8\mu s $
Thời gian để tụ phóng hết điện tích (khi đó điện tích bằng 0) từ giá trị cực đại là $ \dfrac{T}{4}=2\mu s $
Câu 6: Một mạch dao động lí tưởng đang có dao động điện từ tự do với chu kì dao động T. Tại thời điểm $ t=0 $ , điện tích trên một bản tụ điện đạt giá trị cực đại. Điện tích trên tụ điện có giá trị bằng một nửa giá trị ban đầu sau khoảng thời gian ngắn nhất là
- A
- B
- C
- D

Dựa vào vòng tròn lượng giác ta có: $ \Delta \varphi =\dfrac{\pi }{3}\to \Delta t=\dfrac{T}{6} $
Câu 7: Một mạch dao động lí tưởng đang có dao động điện từ tự do với chu kì dao động T. Tại thời điểm $ t=0 $ , điện tích trên một bản tụ điện đạt giá trị cực đại. Điện tích trên bản tụ này bằng 0 ở thời điểm đầu tiên (kể từ $ t=0 $ ) là
- A
- B
- C
- D

Dựa vào vòng tròn lượng giác ta có:
$ \Delta \varphi =\dfrac{\pi }{2}\Rightarrow \Delta t=\dfrac{T}{4} $
Câu 8: Một mạch dao động lí tưởng đang có dao động điện từ tự do với chu kì dao động T. Khoảng thời gian ngắn nhất để điện tích trên bản tụ giảm từ cực đại về nửa giá trị cực đại là
- A
- B
- C
- D
Khoảng thời gian ngắn nhất để điện tích trên bản tụ giảm từ cực đại về nửa giá trị cực đại là: $ \dfrac{T}{6} $ .
Xem thêm các bài tiếp theo bên dưới