Tính chất ba đường phân giác của tam giác
Lý thuyết về Tính chất ba đường phân giác của tam giác
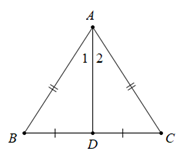
Định lí 1: Trong một tam giác cân, đường phân giác của góc ở đỉnh đồng thời là đường trung tuyến của tam giác đó.
ΔABC:AB=AC^A1=^A2}⇒BD=DC
Định lí 2: Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó.
Tam giác ABC(hình vẽ) có ba đường phân giác giao nhau tại I. Khi đó
{^A1=^A2,^B1=^B2,^C1=^C2ID=IE=IF
Bài tập tự luyện có đáp án
Câu 1: Cho tam giác ABC có ˆC=300 . Tia phân giác của góc B và tia phân giác của góc ngoài đỉnh A cắt nhau ở E. Số đo góc BCE là:
- A
- B
- C
- D

ΔABC có BE là đường phân giác của góc B, AE là đường phân giác ngoài tại A nên CE là đường phân giác góc ngoài tại C.
Do đó: ˆC1=ˆC2=15002=750.
Vậy ^BCE=300+750=1050.
Câu 2: Cho tam giác ABC có các đường phân giác trong của tam giác cắt nhau tại O. Kẻ OD⊥BC (D∈BC) . Kết quả so sánh nào sau đây là đúng?
- A
- B
- C
- D

Kẻ OE⊥AB (E∈AB) .
Vì O là giao điểm của các đường phân giác trong tam giác ABC nên OE=OD . (1)
Xét tam giác AEO vuông tại E có OA là cạnh huyền
⇒OE<OA . (2)
Từ (1) và (2) suy ra OD<OA.
Câu 3: Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Qua I, kẻ đường thẳng song song với AB, cắt AC và BC lần lượt tại D và E. Chọn khẳng định sai.
Chọn khẳng định sai.
- A
- B
- C
- D

Vì các tia phân giác của góc B và góc C cắt nhau tại I nên AI là tia phân giác của góc A
⇒ˆA1=ˆA2.
DE//AB⇒ˆA1=ˆD1⇒ˆA2=ˆD1.
⇒ΔADI cân tại D ⇒AD=DI (1)
Chứng minh tương tự: BE=EI. (2)
Từ (1) và (2) suy ra: AD+BE=DI+EI=DE.
Vậy khẳng định sai cần chọn là: " AD=EI ".
Câu 4: Cho ΔABC có AD là đường phân giác, biết BD=9cm , DC=8cm, AC=10cm . Độ dài cạnh AB bằng
- A
- B
- C
- D
Áp dụng tính chất của tia phân giác trong tam giác ta có
BDCD=ABAC⇒AB=BD.ACCD=9.108=454 cm.
Câu 5: Cho tam giác ABC có các đường phân giác trong của góc B và góc C cắt nhau tại O. Nếu ^BOC=135o thì khẳng định nào sau đây là đúng ?
- A
- B
- C
- D

Xét tam giác BOC có ^BOC=135o ⇒ˆB1+ˆC1=180o−135o=45o
Vì BO là tia phân giác của góc B, CO là tia phân giác của góc C nên ta có:
^ABC+^ACB=2ˆB1+2ˆC1=2(ˆB1+ˆC1)=2.45o=90o .
⇒ΔABC vuông tại A.
Câu 6: Cho tam giác ABC có ˆA=120o có các đường phân giác AD, BE, CF (hình vẽ): 
Cho biết DE=8cm;DF=6cm. Khi đó độ dài EF là:

Cho biết DE=8cm;DF=6cm. Khi đó độ dài EF là:
- A
- B
- C
- D
Vì ^BAC=120o , AD là tia phân giác của ^BAC nên: ˆA1=ˆA2=ˆA3=ˆA4=60o .
- Xét tam giác ABD có AC là tia phân giác ngoài tại đỉnh A, tia BE là tia phân giác trọng của góc B, hai tia phân giác này cắt nhau tại E nên DE là tia phân giác ngoài tại đỉnh D.
- Xét tam giác ADC, chứng minh tương tự ta có DF là tia phân giác ngoài tại đỉnh D.
Từ đó suy ra DE⊥DF tại D ⇒ΔDEF vuông tại D.
Theo định lí Py-ta-go ta có: EF=√DF2+DE2=√82+62=10(cm).
Câu 7: Cho ΔABC đường phân giác AD , biết AB=6cm; AC=9cm; BD=4cm . Độ dài cạnh DC bằng
- A
- B
- C
- D
Áp dụng tính chất của tia phân giác trong tam giác ta có:
BDCD=ABAC⇒CD=BD.ACAB=4.96=6 cm.
Câu 8: Cho tam giác cân ABC có các đường phân giác BD và CE (D∈AC,E∈AB) . Khi đó :
- A
- B
- C
- D

Xét ΔABD và ΔACE có:
AB=AC,ˆB1=ˆC1 (Vì ^ABC=^ACB ), ˆA chung.
⇒ ΔABD=ΔACE(g.c.g)
⇒BD=CE;^AEC=^ADB .
Câu 9: Cho hình vẽ sau, trong đó KO là tia phân giác của ^IKL , LO là tia phân giác của ^ILK . 
Số đo góc ^KOL là:

Số đo góc ^KOL là:
- A
- B
- C
- D
^IKL+^ILK=1800−ˆI=1800−620=1180.
Vì KO, LO lần lượt là tia phân giác của ^IKL và ^ILK nên
ˆK1+ˆL1=ˆK+ˆL2=590.⇒^KOL=1800−(ˆK1+ˆL1)=1800−590=1210.
Câu 10: Cho ΔABC cân tại A . Gọi G là trọng tâm tam giác, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Khẳng định nào dưới đây là đúng?
- A
- B
- C
- D
Do I nằm trong tam giác và cách đều ba cạnh của tam giác nên I thuộc trung tuyến kẻ từ A .
ΔABC cân tại A mà G là trọng tâm nên G thuộc trung tuyến kẻ từ A .
⇒ A, G, I thẳng hàng.
Câu 11: Cho tam giác ABC có I là giao điểm của các tia phân giác của các góc B và góc C. Gọi D là giao điểm của AI và BC. Kẻ IH vuông góc với BC (H∈BC) . Khi đó:
- A
- B
- C
- D

Vì các đường phân giác của góc B và góc C cắt nhau tại I nên AI là tia phân giác của ^BAC .
Ta có: ^BIH=900−ˆB1=900−^ABC2 (1)
^CID=ˆA2+ˆC2=^BAC2+^ACB2=900−^ABC2. (2)
Từ (1) và (2) suy ra ^BIH=^CID.
Câu 12: Cho ΔABC cân tại A , đường trung tuyến AM và đường phân giác BD cắt nhau tại K . Gọi E là giao điểm của CK và AB . Khẳng định nào dưới đây là sai?
- A
- B
- C
- D
Do ΔABC cân tại A nên AM vừa là đường trung tuyến, vừa là phân giác kẻ từ đỉnh A của ΔABC⇒K cách đều các cạnh của ΔABC .
K là giao của 3 đường phân giác của tam giác ΔABC
CE là đường phân giác của ^ACB .
Câu 13: Cho tam giác ABC có ˆA=1000,ˆB=500. Tia phân giác trong tại đỉnh B cắt tia phân giác ngoài tại đỉnh C của tam giác ABC tại O. Số đo ^BCO là:
- A
- B
- C
- D

Gọi I là giao điểm của ba đường phân giác trong của ΔABC.
Xét ΔABC có ˆA=1000,ˆB=500⇒ˆC=300⇒ˆC1=150.
Ta có: CO⊥CI (hai tia phân giác của hai góc kề bù).
⇒^OCI=900.
Khi đó: ^BCO=ˆC1+^OCI=150+900=1050 .
Câu 14: Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H∈BC) . Các tia phân giác của ^HAC và ^AHC cắt nhau ở I. Tia phân giác của ^HAB cắt BC ở D. Chọn khẳng định sai.
Chọn khẳng định sai.
- A
- B
- C
- D

^CAD phụ với góc ˆA1,^ADC phụ với góc ˆA2 mà ˆA1=ˆA2 nên ^CAD=^ADC.
Suy ra ΔACD cân tại C. (1)
Tam giác AHC có các đường phân giác AI và HI cắt nhau ở I nên CI là đường phân giác của góc C. (2)
Từ (1) và (2) suy ra CI đi qua trung điểm của cạnh đáy AD.