Động lượng
Lý thuyết về Động lượng
Động lượng $\overrightarrow{p}$của một vật là một véc tơ cùng hướng với vận tốc và được xác định bởi công thức:$\overrightarrow{p}=m\overrightarrow{v}$
Đơn vị động lượng là \[kgm/s=N.s\]
Độ biến thiên động lượng của một vật trong khoảng thời gian \[\Delta t\] bằng xung lượng của tổng các lực tác dụng lên vật trong khoảng thời gian đó.
$\overrightarrow{{{p}_{2}}}-\overrightarrow{{{p}_{1}}}=\overrightarrow{F}\Delta t$ hay $\Delta \overrightarrow{p}=\overrightarrow{F}\Delta t$
- Một hệ nhiều vật được gọi là cô lập khi không có ngoại lực tác dụng lên hệ hoặc nếu có thì các ngoại lực ấy cân bằng nhau.
- Trong hệ cô lập chỉ có nội lực tương tác giữa các vật trong hệ trực đối nhau từng đôi một.
Động lượng của hệ vật.
$\overrightarrow{p}=\overrightarrow{{{p}_{1}}}+\overrightarrow{{{p}_{2}}}$
Khi $\overrightarrow{{{p}_{1}}}\uparrow \uparrow \overrightarrow{{{p}_{2}}}\Rightarrow p={{p}_{1}}+{{p}_{2}}$
Khi $\overrightarrow{{{p}_{1}}}\uparrow \downarrow \overrightarrow{{{p}_{2}}}\Rightarrow p=\left| {{p}_{1}}-{{p}_{2}} \right|$
Khi $\overrightarrow{{{p}_{1}}}\bot \overrightarrow{{{p}_{2}}}\Rightarrow p=\sqrt{p_{1}^{2}+p_{2}^{2}}$
Khi $\left( \overrightarrow{{{p}_{1}}};\overrightarrow{{{p}_{2}}} \right)=\alpha \Rightarrow {{p}^{2}}=p_{1}^{2}+p_{2}^{2}+2{{p}_{1}}{{p}_{2}}\cos \alpha $
Bài tập tự luyện có đáp án
Câu 1: Một hòn đá được ném xiên một góc $ {{30}^ 0 } $ so với phương ngang với động lượng ban đầu có độ lớn bằng 2 kg.m/s từ mặt đất, bỏ qua sức cản của không khí. Bỏ qua sức cản của môi trường, độ biến thiên động lượng khi hòn đá rơi tới mặt đất có giá trị là:
- A
- B
- C
- D
Độ biến thiên động lượng của vật là: $ \Delta \overrightarrow p =\overrightarrow{p'}-\overrightarrow p $
Xét theo phương ngang, vật chuyển động thẳng đều nên động lượng theo phương Ox không đổi, ta có: $ \Delta { p _ x }=0 $
Xét theo phương thẳng đứng, vận tốc lúc ném lên và lúc chạm đất có độ lớn bằng nhau và ngược hướng. Ta có:
$ \begin{array}{l} & { p _ y }=p.\sin {{30}^ 0 }=2.\sin {{30}^ 0 }=1\left( kg.m/s \right) \\ & { p _ y }'=-{ p _ y }=-1\left( kg.m/s \right) \\ & \Delta p=\Delta { p _ y }={ p _ y }'-{ p _ y }=-1-1=-2\left( kg.m/s \right) \\ \end{array} $
Độ biến thiên động lượng khi hòn đá rơi tới mặt đất có giá trị là 2 kg.m/s
Câu 2: Phương trình của định luật bảo toàn động lượng cho trường hợp hệ nhiều vật :
- A
- B
- C
- D
Ở trạng thái 1, tổng động lượng của hệ n vật là: $ \overrightarrow p =\overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }}+...+\overrightarrow{{ p _ n }} $
Ở trạng thái 2, tổng động lượng của hệ n vật là: $ \overrightarrow{p'}=\overrightarrow{{ p _ 1 }}'+\overrightarrow{{ p _ 2 }}'+...+\overrightarrow{{ p _ n }}' $
Định luật bảo toàn động lượng: $ \overrightarrow p =\overrightarrow{p'}\Leftrightarrow \overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }}+...+\overrightarrow{{ p _ n }}=\overrightarrow{{ p _ 1 }}'+\overrightarrow{{ p _ 2 }}'+...+\overrightarrow{{ p _ n }}' $
Câu 3: Một hệ gồm hai vật A và B có khối lượng lần lượt là 2 kg và 4 kg. Vật A chuyển động theo chiều âm của trục tọa độ Ox với tốc độ 3 m/s. Vật B chuyển động theo chiều dương của trục tọa độ Oy với tốc độ 2 m/s. Động lượng của cả hệ có giá trị là:
- A
- B
- C
- D
Động lượng của vật A là: $ { p _ 1 }={ m _ 1 }{ v _ 1 } $
Động lượng của vật B là: $ { p _ 2 }={ m _ 2 }{ v _ 2 } $
Động lượng của hệ 2 vật là: $ \overrightarrow p =\overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }} $
$ \Rightarrow \overrightarrow{{ v _ 1 }}\bot \overrightarrow{{ v _ 2 }}\Rightarrow \overrightarrow{{ p _ 1 }}\bot \overrightarrow{{ p _ 2 }}\Rightarrow p=\sqrt{{{\left( { m _ 1 }{ v _ 1 } \right)}^ 2 }+{{\left( { m _ 2 }{ v _ 2 } \right)}^ 2 }}=\sqrt{{{\left( 2.3 \right)}^ 2 }+{{\left( 4.2 \right)}^ 2 }}=10\left( kg.m/s \right) $
Câu 4: Tổng động lượng của một hệ không bảo toàn khi nào?
- A
- B
- C
- D
Hệ chuyển động có ma sát: trong quá trình chuyển động, vật chịu tác dụng của lực ma sát là ngoại lực nên hệ không phải là hệ cô lập, tổng động lượng của hệ không bảo toàn.
Câu 5: Một hệ gồm hai vật A và B có khối lượng lần lượt là 2 kg và 3 kg. Vật A chuyển động theo chiều âm của trục tọa độ Ox với tốc độ 5 m/s. Vật B chuyển động theo chiều dương của trục tọa độ Ox với tốc độ 7 m/s. Động lượng của cả hệ có giá trị là:
- A
- B
- C
- D
Động lượng của vật A là: $ { p _ 1 }={ m _ 1 }{ v _ 1 } $
Động lượng của vật B là: $ { p _ 2 }={ m _ 2 }{ v _ 2 } $
Động lượng của hệ 2 vật là: $ \overrightarrow p =\overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }} $
Chiếu lên trục Ox, ta có: $ p=-{ p _ 1 }+{ p _ 2 }=-{ m _ 1 }{ v _ 1 }+{ m _ 2 }{ v _ 2 }=-2.5+3.7=11\left( kg.m/s \right) $
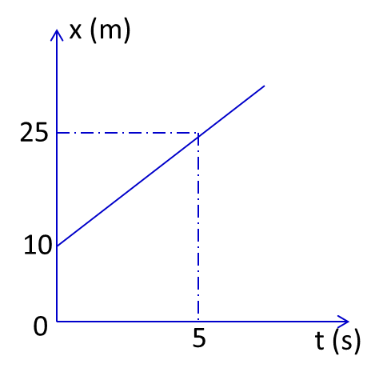
Câu 6: Trên hình vẽ bên là đồ thị tọa độ – thời gian của một vật có khối lượng 2 kg. Động lượng của vật tại thời điểm t = 5 s là


- A
- B
- C
- D
Thời điểm t = 0 đến thời điểm t = 5 s, vật chuyển động thẳng đều với vận tốc là:
$ v=\dfrac{\Delta x}{\Delta t}=\dfrac{25-10} 5 =3\left( m/s \right) $
Động lượng của vật tại thời điểm t = 5 s là: $ p=mv=2.3=6\left( kg.m/s \right) $
Câu 7: Hệ gồm hai vật có động lượng là $ { m _ 1 }=3kg $ , chuyển động với vận tốc $ { v _ 1 }=2m/s $ , vật thứ hai có khối lượng $ { m _ 2 }=2kg $ chuyển động với vận tốc $ { v _ 2 }=4m/s $ . Động lượng tổng cộng của hệ là 14 kg.m/s nếu:
- A
- B
- C
- D
Động lượng của vật 1 có độ lớn là: $ { p _ 1 }={ m _ 1 }{ v _ 1 }=3.2=6\left( kg.m/s \right) $
Động lượng của vật 2 có độ lớn là: $ { p _ 2 }={ m _ 2 }{ v _ 2 }=2.4=8\left( kg.m/s \right) $
Động lượng của hệ 2 vật là: $ \overrightarrow p =\overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }} $
$ \left( \widehat{\overrightarrow{{ v _ 1 }};\overrightarrow{{ v _ 2 }}} \right)=\alpha \Rightarrow \left( \widehat{\overrightarrow{{ p _ 1 }};\overrightarrow{{ p _ 2 }}} \right)=\alpha \Rightarrow p=\sqrt{p_ 1 ^ 2 +p_ 2 ^ 2 +2{ p _ 1 }{ p _ 2 }\text{cos}\alpha } $
$ \Leftrightarrow 14=\sqrt{{ 6 ^ 2 }+{ 8 ^ 2 }+2.6.8.\text{cos}\alpha }\Leftrightarrow \text{cos}\alpha =1\Rightarrow \alpha ={ 0 ^ 0 } $
→ Hai véctơ $ \overrightarrow{{ v _ 1 }} $ và $ \overrightarrow{{ v _ 2 }} $ cùng phương, cùng chiều.
Câu 8: Chọn câu phát biểu đúng. Định luật bảo toàn động lượng chỉ đúng trong trường hợp:
Định luật bảo toàn động lượng chỉ đúng trong trường hợp:
- A
- B
- C
- D
Sách giáo khoa VL 10, trang 125: "Động lượng của một hệ cô lập là một đại lượng bảo toàn".
Câu 9: Đơn vị của động lượng là
- A
- B
- C
- D
Độ lớn của động lượng được xác định theo công thức: \(p = mv\).
Đơn vị của động lượng là: \(kg.m/s\).
Câu 10: Khi gia tốc của vật tăng gấp 3 lần thì động lượng.
- A
- B
- C
- D
Động lượng không phụ thuộc vào gia tốc.
Câu 11: Một vật có khối lượng m = 2kg, chuyển động theo phương trình: $ x=7-8t+{ t ^ 2 } $ (m và s). Động lượng của vật tại thời điểm t = 2 s là:
- A
- B
- C
- D
Ta có: $ x=7-8t+{ t ^ 2 }\Rightarrow \left\{ \begin{array}{l} & { v _ 0 }=-8m/s \\ & \dfrac{a}{2} =1\Rightarrow a=2m/{ s ^ 2 } \\ \end{array} \right. $
Phương trình vận tốc: $ v={ v _ 0 }+at=-8+2t\ (m/s) $
Tại thời điểm t = 2 s, vận tốc của vật là: $ v=-8+2.2=-4\ (m/s) $
Động lượng của vật là: $ p=mv=2.\left( -4 \right)=-8\ (kgm/s) $
Câu 12: Định luật bảo toàn động lượng phát biểu:
- A
- B
- C
- D
Sách giáo khoa VL 10, trang 125: "Động lượng của một hệ cô lập là một đại lượng bảo toàn".
Câu 13: Một vật có khối lượng 20kg bắt đầu chuyển động không ma sát trên mặt phẳng nằm ngang dưới tác dụng của một lực kéo có độ lớn F = 20 N. Tính động lượng của vật khi nó chuyển động được quãng đường 8 m.
- A
- B
- C
- D
Áp dụng định luật II Niutơn ta có: $ a=\dfrac{F}{m} =\dfrac{20}{20}=1\left( m/{ s ^ 2 } \right) $
Từ biểu thức: $ { v ^ 2 }-v_ 0 ^ 2 =2\text{as}\Rightarrow v=\sqrt{2\text{as}}=\sqrt{2.1.8}=4\left( m/s \right) $
Động lượng của vật là: $ p=mv=20.4=80\left( kg.m/s \right) $
Câu 14: Phát biểu nào dưới đây là không đúng? Trong một hệ kín
- A
- B
- C
- D
Trong một hệ cô lập, chỉ có các nội lực tương tác với nhau và chúng trực đối từng đôi một. Hệ cô lập không có ngoại lực tác động hoặc nếu có thì các ngoại lực cân bằng nhau.
Câu 15: Động lượng của hệ được bảo toàn khi.
- A
- B
- C
- D
Động lượng của hệ cô lập được bảo toàn. Hệ vật được coi là hệ cô lập khi không chịu tác dụng của ngoại lực.
Câu 16: Phát biểu nào sau đây không đúng?
- A
- B
- C
- D
Đơn vị của động lượng là kg. m/s
Câu 17: Chọn hình vẽ thể hiện đúng mối quan hệ giữa vectơ động lượng và véctơ vận tốc của một chất điểm.
- A
- B
- C
- D
Biểu thức động lượng: $ \overrightarrow p =m\overrightarrow v $
Do m là một đại lượng vô hướng và luôn dương, do đó véctơ động lượng luôn cùng phương, cùng chiều với véctơ vận tốc.
Câu 18: Một hệ gồm hai vật: vật thứ nhất có khối lượng $ { m _ 1 }=2kg $ , chuyển động với vận tốc $ { v _ 1 }=3m/s $ , vật thứ hai có khối lượng $ { m _ 2 } $ chuyển động với vận tốc $ { v _ 2 }=4m/s $ theo hướng vuông góc với hướng chuyển động của vật thứ nhất. Động lượng của hệ có độ lớn là 10 kg.m/s. Giá trị của $ { m _ 2 } $ là
- A
- B
- C
- D
Động lượng của vật 1 có độ lớn là: $ { p _ 1 }={ m _ 1 }{ v _ 1 }=2.3=6\left( kg.m/s \right) $
Động lượng của vật 2 có độ lớn là: $ { p _ 2 }={ m _ 2 }{ v _ 2 }=8{ m _ 2 }\left( kg.m/s \right) $
Động lượng của hệ 2 vật là: $ \overrightarrow p =\overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }} $
$ \overrightarrow{{ v _ 1 }}\bot \overrightarrow{{ v _ 2 }}\Rightarrow \overrightarrow{{ p _ 1 }}\bot \overrightarrow{{ p _ 2 }}\Rightarrow p=\sqrt{p_ 1 ^ 2 +p_ 2 ^ 2 }=\sqrt{{ 6 ^ 2 }+{{\left( 4{ m _ 2 } \right)}^ 2 }}=10\Rightarrow { m _ 2 }=2(kg) $
Câu 19: Một hệ gồm hai vật có độ lớn động lượng lần lượt là $ { p _ 1 }=6kg.m/s $ và $ { p _ 2 }=4kg.m/s $ . Biết vận tốc của chúng cùng phương, ngược chiều nhau. Độ lớn động lượng của hệ là:
- A
- B
- C
- D
Động lượng của hệ là: $ \overrightarrow p =\overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }} $
$ \overrightarrow{{ v _ 1 }}\uparrow \downarrow \overrightarrow{{ v _ 2 }}\Rightarrow \overrightarrow{{ p _ 1 }}\uparrow \downarrow \overrightarrow{{ p _ 2 }}\Rightarrow p=\left| { p _ 1 }-{ p _ 2 } \right|=6-4=2\left( kg.m/s \right) $
Câu 20: Một máy bay có khối lượng 160000kg, bay với vận tốc 870km/h thì động lượng của máy bay là bao nhiêu ?
- A
- B
- C
- D
$ v=870\left( km/h \right)=\dfrac{725} 3 \left( m/s \right) $
Động lượng của máy bay là: $ p=mv=160000.\dfrac{725} 3 =38,{{7.10}^ 6 }\left( kg.m/s \right) $
Câu 21: Ném một vật từ độ cao h theo phương thẳng đứng xuống đất với vận tốc ban đầu là 20 m/s. Tìm h để động lượng của vật lúc chạm đất gấp 3 lần động lượng của nó lúc ở độ cao h. Lấy $ g=10m/{ s ^ 2 } $ .
- A
- B
- C
- D
Động lượng của vật khi ở độ cao h là: $ p=m{ v _ 0 }=20m $ .
Tốc độ của vật lúc chạm đất là: $ { v ^ 2 }-v_ 0 ^ 2 =2\text g h\Rightarrow v=\sqrt{v_ 0 ^ 2 +2\text a h}=\sqrt{{{20}^ 2 }+2.\text{10}\text . h} $
Động lượng của vật khi chạm đất là: $ p'=m\sqrt{{{20}^ 2 }+2.\text{10}\text . h} $ .
Để p’ = 3p, ta có:
$ m\sqrt{{{20}^ 2 }+2.\text{10}\text . h}=3.20m\Leftrightarrow {{20}^ 2 }+2.\text{10}\text . h={{60}^ 2 }\Rightarrow h=160m $
Câu 22: $ \sum{{{\overrightarrow p }_ t }} $ là tổng động lượng của hệ lúc đầu, $ \sum{{{\overrightarrow p }_ s }} $ là tổng động lượng của hệ lúc sau. Coi hệ là hệ cô lập, ta có.
- A
- B
- C
- D
Động lượng của hệ cô lập được bảo toàn, nên tổng động lượng lúc đầu bằng tổng động lượng lúc sau.
Câu 23: Chọn câu phát biểu sai :
- A
- B
- C
- D
Hệ vật – Trái Đất chỉ gần đúng là hệ kín vì vẫn luôn tồn tại các lực hấp dẫn từ các thiên thể trong vũ trụ tác dụng lên hệ.
Câu 24: Hệ vật –Trái Đất chỉ gần đúng là hệ kín vì:
- A
- B
- C
- D
Hệ vật – Trái Đất chỉ gần đúng là hệ kín vì vẫn luôn tồn tại các lực hấp dẫn từ các thiên thể trong vũ trụ tác dụng lên hệ.
Câu 25: Ném một vật từ độ cao 20 m theo phương thẳng đứng xuống đất với vận tốc ban đầu là v0. Tìm v0 để động lượng của vật lúc chạm đất gấp 4 lần động lượng của nó lúc ở độ cao h. Lấy $ g=10m/{ s ^ 2 } $ .
- A
- B
- C
- D
Động lượng của vật khi ở độ cao 20 m là: $ p=m{ v _ 0 } $ .
Tốc độ của vật lúc chạm đất là: $ { v ^ 2 }-v_ 0 ^ 2 =2\text g h\Rightarrow v=\sqrt{v_ 0 ^ 2 +2\text a h}=\sqrt{v_ 0 ^ 2 +2.\text{10}.20}=\sqrt{v_ 0 ^ 2 +400} $
Động lượng của vật khi chạm đất là: $ p'=m\sqrt{v_ 0 ^ 2 +400} $ .
Để p’ = 4p, ta có:
$ m\sqrt{v_ 0 ^ 2 +400}=4.m{ v _ 0 }\Leftrightarrow v_ 0 ^ 2 +400=16v_ 0 ^ 2 \Rightarrow { v _ 0 }=26,7\left( m/s \right) $
Câu 26: Trong các trường hợp nào sau đây động lượng của vật được bảo toàn:
- A
- B
- C
- D
+ Vật chuyển động thẳng đều: theo định luật III Niutơn, tổng các lực tác dụng lên vật triệt tiêu nên hệ là hệ kín, động lượng của vật được bảo toàn.
+ Vật được ném thẳng đứng lên cao, vật rơi tự do, vật ném ngang: trong quá trình chuyển động vật chịu tác dụng của ngoại lực là trọng lực nên hệ không phải là kín, động lượng của vật không bảo toàn.
Câu 27: Trường hợp nào động lượng không thay đổi theo thời gian?
- A
- B
- C
- D
Chỉ trong trường hợp chuyển động thẳng đều, vecto vận tốc không đổi nên vecto động lượng cũng không đổi.
Câu 28: Động lượng của một vật không phụ thuộc vào
- A
- B
- C
- D
Động lượng của một vật chỉ phụ thuộc vào khối lượng, vận tốc và hệ qui chiếu được chọn.
Câu 29: Hai viên đạn khối lượng lần lượt là 5g và 10g được bắn với cùng vận tốc. Tỉ số động lượng viên đạn thứ hai so với viên đạn 1 là:
- A
- B
- C
- D
$ { v _ 1 }={ v _ 2 }=v\Rightarrow \left\{ \begin{array}{l} & { p _ 1 }={ m _ 1 }v \\ & { p _ 2 }={ m _ 2 }v \\ \end{array} \right.\Rightarrow \dfrac{{ p _ 2 }}{{ p _ 1 }}=\dfrac{{ m _ 2 }}{{ m _ 1 }}=\dfrac{10} 5 =2 $
Câu 30: Một ô tô con có khối lượng 2 tấn chạy nhanh dần đều, sau 50s đi được 400m. Tiếp ngay sau đó 10s ô tô có động lượng là
- A
- B
- C
- D
Chọn chiều dương là chiều chuyển động của ô tô.
Ở thời điểm $ { t _ 1 }=50s $ , ta có: $ s=\dfrac{a{ t ^ 2 }} 2 \Leftrightarrow 400=\dfrac{a{{.50}^ 2 }} 2 \Rightarrow a=0,32\left( m/{ s ^ 2 } \right) $ .
Ở thời điểm $ { t _ 2 }={ t _ 1 }+10=50+10=60\left( \text s \right) $ thì $ v=at=0,32.60=19,2\left( m/s \right) $
Động lượng: $ p=mv=2000.19,2=38400\left( kg.m/s \right) $
Câu 31: Một vật khối lượng 1 kg chuyển động tròn đều với tốc độ 10 m/s. Độ biến thiên động lượng của vật sau 1/4 chu kì kể từ lúc bắt đầu chuyển động bằng
- A
- B
- C
- D

Vật chuyển động tròn đều nên động lượng của vật không đổi: p = mv = 1.10 = 10 (kg.m/s)
Biến thiên động lượng của vật là: $ \Delta \overrightarrow p =\overrightarrow{{ p _ 2 }}-\overrightarrow{{ p _ 1 }} $
Khi chất điểm chuyển động trên đường tròn thì vectơ vận tốc tại mỗi vị trí có phương tiếp tuyến với quỹ đạo.
Sau 1/4 chu kì kể từ lúc bắt đầu chuyển động thì góc quay của bán kính là $ {}^{\pi }/{}_ 2 $
Nên $ \overrightarrow{{ v _ 1 }}\bot \overrightarrow{{ v _ 2 }}\Rightarrow \overrightarrow{{ p _ 1 }}\bot \overrightarrow{{ p _ 2 }}\Rightarrow \Delta p=\sqrt{p_ 1 ^ 2 +p_ 2 ^ 2 }=p\sqrt{2} =10\sqrt{2} \left( kg.m/s \right) $
Câu 32: Một hệ gồm hai vật: vật thứ nhất có khối lượng $ { m _ 1 } $ , chuyển động với vận tốc $ { v _ 1 }=2m/s $ , vật thứ hai có khối lượng $ { m _ 2 }=1kg $ chuyển động với vận tốc $ { v _ 2 }=4m/s $ cùng hướng với hướng chuyển động của vật thứ nhất. Động lượng của hệ có độ lớn là 7 kg.m/s. Giá trị của $ { m _ 1 } $ là
- A
- B
- C
- D
Động lượng của vật 1 có độ lớn là: $ { p _ 1 }={ m _ 1 }{ v _ 1 }=2{ m _ 1 }\left( kg.m/s \right) $
Động lượng của vật 2 có độ lớn là: $ { p _ 2 }={ m _ 2 }{ v _ 2 }=1.4=4\left( kg.m/s \right) $
Động lượng của hệ 2 vật là: $ \overrightarrow p =\overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }} $
$ \overrightarrow{{ v _ 1 }}\uparrow \uparrow \overrightarrow{{ v _ 2 }}\Rightarrow \overrightarrow{{ p _ 1 }}\uparrow \uparrow \overrightarrow{{ p _ 2 }}\Rightarrow p={ p _ 1 }+{ p _ 2 }=2{ m _ 1 }+4=7\Rightarrow { m _ 1 }=1,5\left( kg \right) $
Câu 33: Một quả bóng khối lượng 200 g đang bay với vận tốc v = 20 m/s thì đập vào một bức tường thẳng đứng theo phương nghiêng góc $ {{30}^ 0 } $ so với mặt tường. Biết rằng vận tốc của quả bóng ngay sau khi bật trở lại là v’ = 20 m/s và cũng nghiêng với tường một góc $ {{30}^ 0 } $ . Độ biến thiên động lượng của quả bóng có giá trị là:
- A
- B
- C
- D

Động lượng của bóng trước va chạm có độ lớn bằng độ lớn động lượng sau va chạm, ta có: $ { p _ 1 }={ p _ 2 }={ m _ 1 }{ v _ 1 }=0,2.20=4\left( kg.m/s \right) $
Độ biến thiên động lượng của vật là: $ \Delta \overrightarrow p =\overrightarrow{{ p _ 2 }}-\overrightarrow{{ p _ 1 }} $
$ \left( \widehat{\overrightarrow{{ v _ 1 }};\overrightarrow{{ v _ 2 }}} \right)={{60}^ 0 }\Rightarrow \left( \widehat{\overrightarrow{{ p _ 1 }};\overrightarrow{{ p _ 2 }}} \right)={{60}^ 0 } $
$ \Rightarrow \Delta p=\sqrt{p_ 1 ^ 2 +p_ 2 ^ 2 -2{ p _ 1 }{ p _ 2 }\text{cos}{{60}^ 0 }}=\sqrt{{ 4 ^ 2 }+{ 4 ^ 2 }-2.4.4.\text{cos}{{60}^ 0 }}=4\left( kg.m/s \right) $
Câu 34: Một quả bóng khối lượng 200 g đang bay với vận tốc v = 20 m/s thì đập vào một bức tường thẳng đứng theo phương nghiêng góc $ {{60}^ 0 } $ so với mặt tường. Biết rằng vận tốc của quả bóng ngay sau khi bật trở lại là v’ = 20 m/s và cũng nghiêng với tường một góc $ {{60}^ 0 } $ . Độ biến thiên động lượng của quả bóng có giá trị là:
- A
- B
- C
- D

Động lượng của bóng trước va chạm có độ lớn bằng độ lớn động lượng sau va chạm, ta có: $ { p _ 1 }={ p _ 2 }={ m _ 1 }{ v _ 1 }=0,2.20=4\left( kg.m/s \right) $
Độ biến thiên động lượng của vật là: $ \Delta \overrightarrow p =\overrightarrow{{ p _ 2 }}-\overrightarrow{{ p _ 1 }} $
$ \left( \widehat{\overrightarrow{{ v _ 1 }};\overrightarrow{{ v _ 2 }}} \right)={{120}^ 0 }\Rightarrow \left( \widehat{\overrightarrow{{ p _ 1 }};\overrightarrow{{ p _ 2 }}} \right)={{120}^ 0 } $
$ \Rightarrow \Delta p=\sqrt{p_ 1 ^ 2 +p_ 2 ^ 2 -2{ p _ 1 }{ p _ 2 }\text{cos}{{120}^ 0 }}=\sqrt{{ 4 ^ 2 }+{ 4 ^ 2 }-2.4.4.\text{cos}{{120}^ 0 }}=4\sqrt{3} \left( kg.m/s \right) $
Câu 35: Một viên đá khối lượng 500 g rơi tự do từ độ cao 20 m so với mặt đất. Lấy $ g=10m/{ s ^ 2 } $ . Động lượng của viên đá khi chạm đất là
- A
- B
- C
- D
Tốc độ của viên đá khi chạm đất là: $ v=\sqrt{2gh}=\sqrt{2.10.20}=20\left( m/s \right) $
Động lượng của viên đá khi chạm đất là: $ p=mv=0,5.20=10\left( kg.m/s \right) $
Câu 36: Chọn câu phát biểu sai :
- A
- B
- C
- D
Biểu thức động lượng: $ \overrightarrow p =m\overrightarrow v $
Do m là một đại lượng vô hướng và luôn dương, do đó véctơ động lượng luôn cùng hướng với véctơ vận tốc.
Câu 37: Hệ gồm hai vật có động lượng là $ { m _ 1 }=3kg $ , chuyển động với vận tốc $ { v _ 1 }=2m/s $ , vật thứ hai có khối lượng $ { m _ 2 }=2kg $ chuyển động với vận tốc $ { v _ 2 }=4m/s $ . Động lượng tổng cộng của hệ là $ 2\sqrt{37} $ kg.m/s nếu:
- A
- B
- C
- D
Động lượng của vật 1 có độ lớn là: $ { p _ 1 }={ m _ 1 }{ v _ 1 }=3.2=6\left( kg.m/s \right) $
Động lượng của vật 2 có độ lớn là: $ { p _ 2 }={ m _ 2 }{ v _ 2 }=2.4=8\left( kg.m/s \right) $
Động lượng của hệ 2 vật là: $ \overrightarrow p =\overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }} $
$ \left( \widehat{\overrightarrow{{ v _ 1 }};\overrightarrow{{ v _ 2 }}} \right)=\alpha \Rightarrow \left( \widehat{\overrightarrow{{ p _ 1 }};\overrightarrow{{ p _ 2 }}} \right)=\alpha \Rightarrow p=\sqrt{p_ 1 ^ 2 +p_ 2 ^ 2 +2{ p _ 1 }{ p _ 2 }\text{cos}\alpha } $
$ \Leftrightarrow 2\sqrt{37}=\sqrt{{ 6 ^ 2 }+{ 8 ^ 2 }+2.6.8.\text{cos}\alpha }\Leftrightarrow \text{cos}\alpha =\dfrac{1}{2} \Rightarrow \alpha ={{60}^ 0 } $
→ Hai véctơ $ \overrightarrow{{ v _ 1 }} $ và $ \overrightarrow{{ v _ 2 }} $ hợp với nhau góc $ {{60}^ 0 } $
Câu 38: Một vật trọng lượng 1N có động lượng 1kg.m/s, lấy $ g=10m/{ s ^ 2 } $ khi đó vận tốc của vật bằng bao nhiêu?
- A
- B
- C
- D
Biểu thức trong lượng: P = mg
Biểu thức động lượng: p = mv
Ta có: $ \dfrac{p}{P} =\dfrac{v}{g} \Rightarrow v=g.\dfrac{p}{P} =10.\dfrac{1}{1} =10\left( m/s \right) $.
Câu 39: Một hòn đá được ném xiên một góc $ {{30}^ 0 } $ so với phương ngang với động lượng ban đầu có độ lớn bằng 2 kg.m/s từ mặt đất, bỏ qua sức cản của không khí. Bỏ qua sức cản của môi trường, độ biến thiên động lượng khi hòn đá lên đến độ cao cực đại có giá trị là:
- A
- B
- C
- D
Độ biến thiên động lượng của vật là: $ \Delta \overrightarrow p =\overrightarrow{p'}-\overrightarrow p $
+ Xét theo phương ngang, vật chuyển động thẳng đều nên động lượng theo phương Ox không đổi, ta có: $ \Delta { p _ x }=0\quad \left( 1 \right) $
+ Xét theo phương thẳng đứng:
Động lượng lúc ném vật lên là:
$ { p _ y }=p.\sin {{30}^ 0 }=2.\sin {{30}^ 0 }=1\left( kg.m/s \right) $
Khi lên đến độ cao cực đại, vận tốc của vật theo phương thẳng đứng bằng 0 nên:
$ { p _ y }'=0\Rightarrow \Delta { p _ y }={ p _ y }'-{ p _ y }=0-1=-1\left( kg.m/s \right)\quad \left( 2 \right) $
Từ (1) và (2) ta có:
$ \Delta { p _ y }=\sqrt{{{\left( \Delta { p _ x } \right)}^ 2 }+{{\left( \Delta { p _ y } \right)}^ 2 }}=1\left( kg.m/s \right) $
Độ biến thiên động lượng khi hòn đá lên tới độ cao cực đại có giá trị là 1 kg.m/s
Câu 40: Khi một tên lửa chuyển động thì cả vận tốc và khối lượng của nó đều thay đổi. Khi khối lượng giảm một nửa, vận tốc tăng gấp 4 lần thì động lượng của tên lửa
- A
- B
- C
- D
Ta có: $ \left\{ \begin{array}{l} & m'=\dfrac{m}{2} \\ & v'=4v \\ \end{array} \right.\Rightarrow p'=m'v'=\dfrac{m}{2} .4v=2mv $
Khi khối lượng giảm một nửa, vận tốc tăng gấp đôi thì động lượng tăng gấp đôi.
Câu 41: Hai ô tô có cùng khối lượng, chuyển động với các tốc độ 36km/h và 20m/s. Tỉ số động lượng của ô tô 1 so với ô tô 2 là:
- A
- B
- C
- D
36km/h = 10 m/s
$ { m _ 1 }={ m _ 2 }=m\Rightarrow \left\{ \begin{array}{l} & { p _ 1 }=m{ v _ 1 } \\ & { p _ 2 }=m{ v _ 2 } \\ \end{array} \right.\Rightarrow \dfrac{{ p _ 1 }}{{ p _ 2 }}=\dfrac{{ v _ 1 }}{{ v _ 2 }}=\dfrac{10}{20}=\dfrac{1}{2} $
Câu 42: Khi một tên lửa chuyển động thì cả vận tốc và khối lượng của nó đều thay đổi. Khi khối lượng giảm một nửa, vận tốc tăng gấp đôi thì động lượng của tên lửa
- A
- B
- C
- D
Ta có: $ \left\{ \begin{array}{l} & m'=\dfrac{m}{2} \\ & v'=2v \\ \end{array} \right.\Rightarrow p'=m'v'=\dfrac{m}{2} .2v=mv $
Khi khối lượng giảm một nửa, vận tốc tăng gấp đôi thì động lượng của tên lửa không đổi.
Câu 43: Một hệ gồm hai vật: vật thứ nhất có khối lượng $ { m _ 1 }=3kg $ , chuyển động với vận tốc $ { v _ 1 }=4m/s $ , vật thứ hai có khối lượng $ { m _ 2 }=2kg $ chuyển động với vận tốc $ { v _ 2 }=8m/s $ cùng hướng với hướng chuyển động của vật thứ nhất. Động lượng của hệ có độ lớn là:
- A
- B
- C
- D
Động lượng của vật 1 có độ lớn là: $ { p _ 1 }={ m _ 1 }{ v _ 1 }=3.4=12\left( kg.m/s \right) $
Động lượng của vật 2 có độ lớn là: $ { p _ 2 }={ m _ 2 }{ v _ 2 }=2.8=16\left( kg.m/s \right) $
$ \overrightarrow{{ v _ 1 }}\uparrow \uparrow \overrightarrow{{ v _ 2 }}\Rightarrow \overrightarrow{{ p _ 1 }}\uparrow \uparrow \overrightarrow{{ p _ 2 }}\Rightarrow p={ p _ 1 }+{ p _ 2 }=12+16=28\left( kg.m/s \right) $
Câu 44: Quá trình nào sau đây, động lượng của ôtô được bảo toàn?
- A
- B
- C
- D
+ Ô tô tăng tốc: Độ lớn động lượng của ô tô tăng dần do vận tốc tăng.
+ Ô tô chuyển động tròn: Hướng của vectơ vận tốc thay đổi nên động lượng của ô tô không bảo toàn.
+ Ô tô giảm tốc: Độ lớn động lượng của ô tô giảm dần do vận tốc giảm.
+ Ô tô chuyển động thẳng đều: Vectơ động lượng không đổi cả về hướng và độ lớn.
Câu 45: Hệ gồm hai vật có động lượng là $ { m _ 1 }=1,5kg $ , chuyển động với vận tốc $ { v _ 1 }=2m/s $ , vật thứ hai có khối lượng $ { m _ 2 } $ chuyển động với vận tốc $ { v _ 2 }=4m/s $ theo hướng hợp với hướng chuyển động của vật thứ nhất một góc $ {{60}^ 0 } $ . Động lượng tổng cộng của hệ là $ \sqrt{37} $ kg.m/s. Giá trị của $ { m _ 2 } $ là
- A
- B
- C
- D
Động lượng của vật 1 có độ lớn là: $ { p _ 1 }={ m _ 1 }{ v _ 1 }=1,5.2=3\left( kg.m/s \right) $
Động lượng của vật 2 có độ lớn là: $ { p _ 2 }={ m _ 2 }{ v _ 2 }=4{ m _ 2 }\left( kg.m/s \right) $
Động lượng của hệ 2 vật là: $ \overrightarrow p =\overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }} $
$ \left( \widehat{\overrightarrow{{ v _ 1 }};\overrightarrow{{ v _ 2 }}} \right)={{60}^ 0 }\Rightarrow \left( \widehat{\overrightarrow{{ p _ 1 }};\overrightarrow{{ p _ 2 }}} \right)={{60}^ 0 } $
$ \begin{array}{l} & \Rightarrow p=\sqrt{p_ 1 ^ 2 +p_ 2 ^ 2 +2{ p _ 1 }{ p _ 2 }\text{cos}{{60}^ 0 }} \\ & \Leftrightarrow \sqrt{{ 3 ^ 2 }+{{(4{ m _ 2 })}^ 2 }+2.3.4{ m _ 2 }.\text{cos}{{60}^ 0 }}=\sqrt{37} \\ & \Leftrightarrow 16m_ 2 ^ 2 +12{ m _ 2 }-28=0\Rightarrow \left[ \begin{array}{l} & { m _ 2 }=1(kg) \\ & { m _ 2 }=-1,75(kg)\Rightarrow loai \\ \end{array} \right. \\ \end{array} $
Giá trị của $ { m _ 2 } $ là 1 kg.
Câu 46: Động lượng của một vật khối lượng m đang chuyển động với vận tốc $ \overrightarrow v $ là đại lượng được xác định bởi công thức
- A
- B
- C
- D
Sách giáo khoa VL 10, trang 123, biểu thức (23.2):
Động lượng của một vật có khối lượng m, đang chuyển động với vận tốc $ \overrightarrow v $ là đại lượng được xác định bởi công thức: $ \overrightarrow p =m\overrightarrow v $
Câu 47: Một xe tải khối lượng m đang chuyển động với vận tốc v thì tăng tốc. Khi vận tốc của xe tăng gấp 3 lần thì động lượng của vật:
- A
- B
- C
- D
$ v'=3v\Rightarrow p'=mv'=m.3v=3mv $
Câu 48: Một vật có khối lượng m = 1kg đang chuyển động với vận tốc v = 2m/s, động lượng của vật là
- A
- B
- C
- D
Động lượng của vật là: p = mv = 1.2 = 2 (kg.m/s).
Câu 49: Một hệ vật được gọi là hệ kín (hệ cô lập ) nếu :
- A
- B
- C
- D
Sách giáo khoa VL 10, trang 124, mục II.1. Hệ cô lập: "Một hệ nhiều vật được gọi là cô lập khi không có ngoại lực tác dụng lên hệ hoặc nếu có thì các ngoại lực ấy cân bằng nhau".
Câu 50: Một hệ gồm hai vật: vật thứ nhất có khối lượng $ { m _ 1 }=3kg $ , chuyển động với vận tốc $ { v _ 1 }=4m/s $ , vật thứ hai có khối lượng $ { m _ 2 }=2kg $ chuyển động với vận tốc $ { v _ 2 }=8m/s $ theo hướng vuông góc với hướng chuyển động của vật thứ nhất. Động lượng của hệ có độ lớn là:
- A
- B
- C
- D
Động lượng của vật 1 có độ lớn là: $ { p _ 1 }={ m _ 1 }{ v _ 1 }=3.4=12\left( kg.m/s \right) $
Động lượng của vật 2 có độ lớn là: $ { p _ 2 }={ m _ 2 }{ v _ 2 }=2.8=16\left( kg.m/s \right) $
$ \overrightarrow{{ v _ 1 }}\bot \overrightarrow{{ v _ 2 }}\Rightarrow \overrightarrow{{ p _ 1 }}\bot \overrightarrow{{ p _ 2 }}\Rightarrow p=\sqrt{p_ 1 ^ 2 +p_ 2 ^ 2 }=\sqrt{{{12}^ 2 }+{{16}^ 2 }}=20(kg.m/s) $
Câu 51: Một vật có khối lượng m = 2kg, chuyển động theo phương trình: $ x=7-8t+{ t ^ 2 } $ (m và s). Độ biến thiên động lượng của vật từ thời điểm t1 =2s đến thời điểm t2 = 5 s là:
- A
- B
- C
- D
Ta có: $ x=7-8t+{ t ^ 2 }\Rightarrow \left\{ \begin{array}{l} & { v _ 0 }=-8m/s \\ & \dfrac{a}{2} =1\Rightarrow a=2m/{ s ^ 2 } \\ \end{array} \right. $
Phương trình vận tốc: $ v={ v _ 0 }+at=-8+2t\ (m/s) $
Tại thời điểm t1 = 2 s, vận tốc của vật là: $ { v _ 1 }=-8+2.2=-4\ (m/s) $
Tại thời điểm t2 = 5 s, vận tốc của vật là: $ { v _ 2 }=-8+2.5=2\ (m/s) $
Độ biến thiên động lượng của vật từ thời điểm t1 =2s đến thời điểm t2 = 5 s là:
$ \Delta p=m\left( { v _ 2 }-{ v _ 1 } \right)=2\left[ 2-\left( -4 \right) \right]=12\left( kg.m/s \right) $
Câu 52: Chọn câu phát biểu sai.
- A
- B
- C
- D
Sách giáo khoa VL 10, trang 125: "Động lượng của một hệ cô lập (hệ kín) là một đại lượng bảo toàn".
Câu 53: Chọn câu phát biểu đúng. Định luật bảo toàn động lượng tương đương với
Định luật bảo toàn động lượng tương đương với
- A
- B
- C
- D
Định luật bảo toàn động lượng không tương đương với các định luật Niu-tơn
Câu 54: Trường hợp nào sau đây là hệ kín (hệ cô lập ) ?
- A
- B
- C
- D
+ Hai viên bi chuyển động trên mặt phẳng nằm ngang không phải hệ kín vì có lực ma sát là ngoại lực.
+ Hai viên bi chuyển động trên mặt phẳng nghiêng không phải hệ kín vì hai ngoại lực là trọng lực và phản lực không triệt tiêu nhau.
+ Hai viên bi rơi thẳng đứng trong không khí không phải là hệ kín vì hai ngoại lực là trọng lực và lực cản của không khí không triệt tiêu nhau.
+ Hai viên bi chuyển động không ma sát trên mặt phẳng nằm ngang thì hai ngoại lực là trọng lực và phản lực triệt tiêu nhau nên hệ có thể coi là hệ kín.
Câu 55: Một hệ gồm hai vật có độ lớn động lượng lần lượt là $ { p _ 1 }=6kg.m/s $ và $ { p _ 2 }=4kg.m/s $ . Biết vận tốc của hai vật có hướng hợp với nhau một góc $ {{45}^ 0 } $ . Độ lớn động lượng của hệ là:
- A
- B
- C
- D
Động lượng của hệ là: $ \overrightarrow p =\overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }} $
$ \left( \widehat{\overrightarrow{{ v _ 1 }};\overrightarrow{{ v _ 2 }}} \right)={{45}^ 0 }\Rightarrow \left( \widehat{\overrightarrow{{ p _ 1 }};\overrightarrow{{ p _ 2 }}} \right)={{45}^ 0 } $ $ \Rightarrow p=\sqrt{p_ 1 ^ 2 +p_ 2 ^ 2 +2{ p _ 1 }{ p _ 2 }\text{cos}{{45}^ 0 }}=\sqrt{{ 6 ^ 2 }+{ 4 ^ 2 }+2.6.4.\text{cos}{{45}^ 0 }}=9,27(kg.m/s) $
Câu 56: Một hệ gồm hai vật có độ lớn động lượng lần lượt là $ { p _ 1 }=6kg.m/s $ và $ { p _ 2 }=4kg.m/s $ . Biết vận tốc của chúng cùng phương, cùng chiều nhau. Độ lớn động lượng của hệ là:
- A
- B
- C
- D
Động lượng của hệ là: $ \overrightarrow p =\overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }} $
$ \overrightarrow{{ v _ 1 }}\uparrow \uparrow \overrightarrow{{ v _ 2 }}\Rightarrow \overrightarrow{{ p _ 1 }}\uparrow \uparrow \overrightarrow{{ p _ 2 }}\Rightarrow p={ p _ 1 }+{ p _ 2 }=6+4=10\left( kg.m/s \right) $
Câu 57: Một hệ gồm hai vật: vật thứ nhất có khối lượng $ { m _ 1 }=2kg $ , chuyển động với vận tốc $ { v _ 1 }=3m/s $ , vật thứ hai có khối lượng $ { m _ 2 } $ chuyển động với vận tốc $ { v _ 2 }=8m/s $ theo hướng vuông góc với hướng chuyển động của vật thứ nhất. Động lượng của hệ có độ lớn là 10 kg.m/s. Giá trị của $ { m _ 2 } $ là
- A
- B
- C
- D
Động lượng của vật 1 có độ lớn là: $ { p _ 1 }={ m _ 1 }{ v _ 1 }=2.3=6\left( kg.m/s \right) $
Động lượng của vật 2 có độ lớn là: $ { p _ 2 }={ m _ 2 }{ v _ 2 }=8{ m _ 2 }\left( kg.m/s \right) $
Động lượng của hệ 2 vật là: $ \overrightarrow p =\overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }} $
$ \overrightarrow{{ v _ 1 }}\bot \overrightarrow{{ v _ 2 }}\Rightarrow \overrightarrow{{ p _ 1 }}\bot \overrightarrow{{ p _ 2 }}\Rightarrow p=\sqrt{p_ 1 ^ 2 +p_ 2 ^ 2 }=\sqrt{{ 6 ^ 2 }+{{\left( 8{ m _ 2 } \right)}^ 2 }}=10\Rightarrow { m _ 2 }=1(kg) $
Câu 58: Một hệ gồm hai vật: vật thứ nhất có khối lượng $ { m _ 1 }=3kg $ , chuyển động với vận tốc $ { v _ 1 }=4m/s $ , vật thứ hai có khối lượng $ { m _ 2 }=2kg $ chuyển động với vận tốc $ { v _ 2 }=8m/s $ ngược hướng với hướng chuyển động của vật thứ nhất. Động lượng của hệ có độ lớn là:
- A
- B
- C
- D
Động lượng của vật 1 có độ lớn là: $ { p _ 1 }={ m _ 1 }{ v _ 1 }=3.4=12\left( kg.m/s \right) $
Động lượng của vật 2 có độ lớn là: $ { p _ 2 }={ m _ 2 }{ v _ 2 }=2.8=16\left( kg.m/s \right) $
$ \overrightarrow{{ v _ 1 }}\uparrow \downarrow \overrightarrow{{ v _ 2 }}\Rightarrow \overrightarrow{{ p _ 1 }}\uparrow \downarrow \overrightarrow{{ p _ 2 }}\Rightarrow p=\left| { p _ 1 }-{ p _ 2 } \right|=\left| 12-16 \right|=4\left( kg.m/s \right) $
Câu 59: Hệ gồm hai vật có động lượng là $ { m _ 1 }=3kg $ , chuyển động với vận tốc $ { v _ 1 }=2m/s $ , vật thứ hai có khối lượng $ { m _ 2 }=2kg $ chuyển động với vận tốc $ { v _ 2 }=4m/s $ . Động lượng tổng cộng của hệ là 10 kg.m/s nếu:
- A
- B
- C
- D
Động lượng của vật 1 có độ lớn là: $ { p _ 1 }={ m _ 1 }{ v _ 1 }=3.2=6\left( kg.m/s \right) $
Động lượng của vật 2 có độ lớn là: $ { p _ 2 }={ m _ 2 }{ v _ 2 }=2.4=8\left( kg.m/s \right) $
Động lượng của hệ 2 vật là: $ \overrightarrow p =\overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }} $
$ \left( \widehat{\overrightarrow{{ v _ 1 }};\overrightarrow{{ v _ 2 }}} \right)=\alpha \Rightarrow \left( \widehat{\overrightarrow{{ p _ 1 }};\overrightarrow{{ p _ 2 }}} \right)=\alpha \Rightarrow p=\sqrt{p_ 1 ^ 2 +p_ 2 ^ 2 +2{ p _ 1 }{ p _ 2 }\text{cos}\alpha } $
$ \Leftrightarrow 10=\sqrt{{ 6 ^ 2 }+{ 8 ^ 2 }+2.6.8.\text{cos}\alpha }\Leftrightarrow \text{cos}\alpha =0\Rightarrow \alpha ={{90}^ 0 } $
→ Hai véctơ $ \overrightarrow{{ v _ 1 }} $ và $ \overrightarrow{{ v _ 2 }} $ vuông góc với nhau.
Câu 60: Phát biểu nào sau đây là sai ?
- A
- B
- C
- D
Một hệ gọi là hệ kín khi không có ngoại lực hoặc tổng các ngoại lực bằng 0.
Câu 61: Phương trình của định luật bảo toàn động lượng cho trường hợp hệ hai vật :
- A
- B
- C
- D
Ở trạng thái 1, tổng động lượng của hệ 2 vật là: $ \overrightarrow p ={ m _ 1 }\overrightarrow{{ v _ 1 }}+{ m _ 2 }\overrightarrow{{ v _ 2 }} $
Ở trạng thái 2, tổng động lượng của hệ 2 vật là: $ \overrightarrow{p'}={ m _ 1 }\overrightarrow{{ v _ 1 }'}+{ m _ 2 }\overrightarrow{{ v _ 2 }'} $
Định luật bảo toàn động lượng: $ \overrightarrow p =\overrightarrow{p'}\Leftrightarrow { m _ 1 }\overrightarrow{{ v _ 1 }}+{ m _ 2 }\overrightarrow{{ v _ 2 }}={ m _ 1 }\overrightarrow{{ v _ 1 }'}+{ m _ 2 }\overrightarrow{{ v _ 2 }'} $
Câu 62: Một người đứng yên ở vĩ độ $ {{60}^ 0 } $ của Trái đất có động lượng là 11629,63 kg.m/s đối với hệ quy chiếu gắn với tâm Trái đất. Coi Trái đất hình cầu có bán kính 6400 km và chu kì tự quay của Trái đất là 24 giờ. Khối lượng của người đó là?
- A
- B
- C
- D
Khoảng cách từ người đến trục quay của trái đất là:
$ r=R.cos{{60}^ 0 }=6400.cos{{60}^ 0 }=3200km $
Trong hệ quy chiếu gắn với tâm trái đất, người thực hiện chuyển động tròn đều quanh tâm nằm trên trục quay của trái đất, bán kính quỹ đạo là 3200 km. Tốc độ chuyển động của người là:
$ v=\omega R=\dfrac{2\pi } T .R=\dfrac{2\pi }{24.3600}{{.3200.10}^ 3 }=\dfrac{2000\pi }{27}\left( m/s \right) $
Khối lượng của người là: $ m=\dfrac{p}{v} =\dfrac{11629,63}{\dfrac{2000\pi }{27}}=50\left( kg \right) $
Câu 63: Một viên đạn khối lượng 10 g đang bay với vận tốc 100 m/s thì gặp bức tường. Sau khi xuyên qua bức tường thì vận tốc viên đạn còn 60 m/s. Độ biến thiên động lượng của viên đạn có giá trị là:
- A
- B
- C
- D
m = 10 g = 0,01 kg; v = 100 m/s; v’ = 60 m/s;
Độ lớn động lượng của đạn trước khi xuyên tường là: $ p=mv=0,01.100=1\left( kg.m/s \right) $
Độ lớn động lượng của đạn sau khi xuyên tường là: $ p'=mv'=0,01.60=0,6\left( kg.m/s \right) $
Độ biến thiên động lượng của vật là: $ \Delta \overrightarrow p =\overrightarrow{p'}-\overrightarrow p $
$ \overrightarrow v \uparrow \uparrow \overrightarrow{v'}\Rightarrow \overrightarrow p \uparrow \uparrow \overrightarrow{p'}\Rightarrow p=p'-p=0,6-1=-0,4(kg.m/s) $
Câu 64: Một vật khối lượng 1 kg chuyển động tròn đều với tốc độ 10 m/s. Độ biến thiên động lượng của vật sau 1 chu kì kể từ lúc bắt đầu chuyển động bằng
- A
- B
- C
- D
Vật chuyển động tròn đều nên động lượng của vật không đổi: p = mv = 1.10 = 10 (kg.m/s)
Biến thiên động lượng của vật là: $ \Delta \overrightarrow p =\overrightarrow{{ p _ 2 }}-\overrightarrow{{ p _ 1 }} $
Sau một chu kì, vật trở lại đúng trạng thái ban đầu nên $ \overrightarrow{{ p _ 2 }}=\overrightarrow{{ p _ 1 }}\Rightarrow \Delta \overrightarrow p =0 $
Câu 65: Chọn câu phát biểu đúng. Hai vật có cùng khối lượng m, chuyển động với vận tốc có độ lớn bằng nhau. Động lượng của hệ hai vật sẽ được tính theo biểu thức nào sau đây?
- A
- B
- C
- D
Động lượng của vật 1: $ \overrightarrow{{ p _ 1 }}={ m _ 1 }\overrightarrow{{ v _ 1 }} $
Động lượng của vật 2: $ \overrightarrow{{ p _ 2 }}={ m _ 2 }\overrightarrow{{ v _ 2 }} $
Do hai vật có cùngkhối lượng: $ { m _ 1 }={ m _ 2 }=m $ nên: $ \overrightarrow p =m\left( \overrightarrow{{ v _ 1 }}+\overrightarrow{{ v _ 2 }} \right) $
Câu 66: Một vật khối lượng m = 500g chuyển động thẳng theo chiều âm trục tọa độ x với vận tốc 43,2 km/h. Động lượng của vật có giá trị là:
- A
- B
- C
- D
43,2km/h = 12 m/s
Do vật chuyển động theo chiều âm của trục Ox nên v = - 12 m/s.
Giá trị động lượng của vật là: p = mv = 0,5.(-12) = - 6 kg.m/s.
Câu 67: Một vật có khối lượng m = 2kg, chuyển động theo phương trình: $ x=7-8t+{ t ^ 2 } $ (m và s). Động lượng của vật tại thời điểm t = 5 s là:
- A
- B
- C
- D
Ta có: $ x=7-8t+{ t ^ 2 }\Rightarrow \left\{ \begin{array}{l} & { v _ 0 }=-8m/s \\ & \dfrac{a}{2} =1\Rightarrow a=2m/{ s ^ 2 } \\ \end{array} \right. $
Phương trình vận tốc: $ v={ v _ 0 }+at=-8+2t\ (m/s) $
Tại thời điểm t = 5 s, vận tốc của vật là: $ v=-8+2.5=2\ (m/s) $
Động lượng của vật là: $ p=mv=2.2=4\ (kgm/s) $
Câu 68: Phát biểu nào sau đây không đúng?
- A
- B
- C
- D
Biểu thức động lượng: $ \overrightarrow p =m\overrightarrow v $
Do chuyển động tròn đều có tốc độ không đổi nhưng hướng của vận tốc thay đổi trong quá trình chuyển động do đó hướng của động lượng cũng thay đổi, chỉ có độ lớn là không đổi.
Câu 69: Đặc điểm của các nội lực trong một hệ cô lập là.
- A
- B
- C
- D
Theo định luật III Niuton, các nội lực trực đối nhau từng đôi một.
Câu 70:
Trên hình vẽ bên là đồ thị tọa độ – thời gian của một vật có khối lượng 3 kg. Động lượng của vật tại thời điểm $ { t _ 1 }=1s $ và thời điểm $ { t _ 2 }=5s $ lần lượt bằng:


- A
- B
- C
- D
Thời điểm t = 0 đến thời điểm t = 3 s, vật chuyển động thẳng đều với vận tốc là:
$ { v _ 1 }=\dfrac{\Delta x}{\Delta t}=\dfrac{4}{3} \left( m/s \right) $
Động lượng của vật tại thời điểm $ { t _ 1 }=1s $ là: $ { p _ 1 }=m{ v _ 1 }=3.\dfrac{4}{3} =4\left( kg.m/s \right) $
Từ thời điểm t = 3s trở đi, vật đứng yên không chuyển động.
Động lượng tại thời điểm $ { t _ 2 }=5s $ là: $ { p _ 2 }=m{ v _ 2 }=0 $
Câu 71: Chọn câu phát biểu sai :
- A
- B
- C
- D
Vận tốc là đại lượng có tính tương đối, do đó khi ở trạng thái cân bằng tốc độ của vật có thể khác giá trị 0, do đó động lượng của vật có thể khác 0
Câu 72: Hệ gồm hai vật có động lượng là $ { m _ 1 }=3kg $ , chuyển động với vận tốc $ { v _ 1 }=2m/s $ , vật thứ hai có khối lượng $ { m _ 2 }=2kg $ chuyển động với vận tốc $ { v _ 2 }=4m/s $ . Động lượng tổng cộng của hệ là 2 kg.m/s nếu:
- A
- B
- C
- D
Động lượng của vật 1 có độ lớn là: $ { p _ 1 }={ m _ 1 }{ v _ 1 }=3.2=6\left( kg.m/s \right) $
Động lượng của vật 2 có độ lớn là: $ { p _ 2 }={ m _ 2 }{ v _ 2 }=2.4=8\left( kg.m/s \right) $
Động lượng của hệ 2 vật là: $ \overrightarrow p =\overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }} $
$ \left( \widehat{\overrightarrow{{ v _ 1 }};\overrightarrow{{ v _ 2 }}} \right)=\alpha \Rightarrow \left( \widehat{\overrightarrow{{ p _ 1 }};\overrightarrow{{ p _ 2 }}} \right)=\alpha \Rightarrow p=\sqrt{p_ 1 ^ 2 +p_ 2 ^ 2 +2{ p _ 1 }{ p _ 2 }\text{cos}\alpha } $
$ \Leftrightarrow 2=\sqrt{{ 6 ^ 2 }+{ 8 ^ 2 }+2.6.8.\text{cos}\alpha }\Leftrightarrow \text{cos}\alpha =-1\Rightarrow \alpha ={{180}^ 0 } $
→ Hai véctơ $ \overrightarrow{{ v _ 1 }} $ và $ \overrightarrow{{ v _ 2 }} $ cùng phương, ngược chiều.
Câu 73: Khi tăng khối lượng vật lên 2 lần và giảm vận tốc đi 4 lần, thì động lượng thay đổi như thế nào?
- A
- B
- C
- D
Ta có $ p=mv $
$ p'=m'v'=2m.\dfrac v 4 =\dfrac{mv} 2 =\dfrac{p}{2} $
Vậy động lượng giảm 2 lần.
Câu 74: Động lượng là đại lượng véc tơ
- A
- B
- C
- D
Biểu thức động lượng: $ \overrightarrow p =m\overrightarrow v $
Do m là một đại lượng vô hướng và luôn dương, do đó véctơ động lượng luôn cùng phương, cùng chiều với véctơ vận tốc.
Câu 75: Một vật chuyển động thẳng đều thì:
- A
- B
- C
- D
Một vật chuyển động thẳng đều thì:
+ Vận tốc của vật không đổi cả về hướng và độ lớn nên động lượng của vật không đổi.
+ Độ biến thiên động lượng và xung lượng của hợp lực bằng 0: $ \Delta \overrightarrow p =\overrightarrow F .\Delta t=\overrightarrow 0 $
Câu 76: Một vật nặng 0,2 kg được thả rơi tự do từ độ cao 45 m. Sau khi chạm đất, vật nẩy lên với vận tốc bằng 2/3 vận tốc lúc chạm đất. Lấy $ g=10m/{ s ^ 2 } $ . Độ biến thiên động lượng của vật có giá trị là:
- A
- B
- C
- D
m = 0,2 kg; h = 45 m; v’ = 2v/3
Tốc độ của vật trước khi chạm đất là: $ v=\sqrt{2gh}=\sqrt{2.10.45}=30\left( m/s \right) $
Động lượng của vật trước khi chạm đất là: $ p=mv=0,2.30=6\left( kg.m/s \right) $
Tốc độ của vật sau khi va chạm với sàn nhà là: v’ = 2v/3 = 20 m/s
Động lượng của vật sau khi va chạm với sàn nhà là: $ p'=mv'=0,2.20=4\left( kg.m/s \right) $
Độ biến thiên động lượng của vật là: $ \Delta \overrightarrow p =\overrightarrow{p'}-\overrightarrow p $
$ \overrightarrow v \uparrow \downarrow \overrightarrow{v'}\Rightarrow \overrightarrow p \uparrow \downarrow \overrightarrow{p'}\Rightarrow p=p'+p=4+6=10(kg.m/s) $
Câu 77: Một hệ gồm hai vật: vật thứ nhất có khối lượng $ { m _ 1 }=3kg $ , chuyển động với vận tốc $ { v _ 1 }=4m/s $ , vật thứ hai có khối lượng $ { m _ 2 }=2kg $ chuyển động với vận tốc $ { v _ 2 }=8m/s $ hợp với hướng chuyển động của vật thứ nhất một góc $ {{45}^ 0 } $ . Động lượng của hệ có độ lớn là:
- A
- B
- C
- D
Động lượng của vật 1 có độ lớn là: $ { p _ 1 }={ m _ 1 }{ v _ 1 }=3.4=12\left( kg.m/s \right) $
Động lượng của vật 2 có độ lớn là: $ { p _ 2 }={ m _ 2 }{ v _ 2 }=2.8=16\left( kg.m/s \right) $
$ \left( \widehat{\overrightarrow{{ v _ 1 }};\overrightarrow{{ v _ 2 }}} \right)={{45}^ 0 }\Rightarrow \left( \widehat{\overrightarrow{{ p _ 1 }};\overrightarrow{{ p _ 2 }}} \right)={{45}^ 0 } $ $ \Rightarrow p=\sqrt{p_ 1 ^ 2 +p_ 2 ^ 2 +2{ p _ 1 }{ p _ 2 }\text{cos}{{45}^ 0 }}=\sqrt{{{12}^ 2 }+{{16}^ 2 }+2.12.16.\text{cos}{{45}^ 0 }}=25,9(kg.m/s) $
Câu 78: Một vật có khối lượng m = 2kg, có động lượng 6kg.m/s, vật đang chuyển động với vận tốc là
- A
- B
- C
- D
Từ biểu thức động lượng:
$ p=mv\Rightarrow v=\dfrac{p}{m} =\dfrac{6}{2} =3\left( m/s \right) $
Câu 79: Đặc điểm của hệ cô lập là.
- A
- B
- C
- D
Hệ cô lập là hệ không chịu tác dụng của ngoại lực hoặc các ngoại lực cân bằng lẫn nhau.
Câu 80: Chất điểm m chuyển động không vận tốc đầu dưới tác dụng của lực không đổi $ \overrightarrow F $ . Động lượng chất điểm ở thời điểm t là:
- A
- B
- C
- D
Áp dụng biểu thức biến thiên động lượng: $ \Delta \overrightarrow p =\overrightarrow F \Delta t $ .
Tại thời điểm ban đầu vật không có vận tốc, nên động lượng của vật tại thời điểm t là: $ \overrightarrow p =\overrightarrow F t $
Câu 81: Một hệ gồm hai vật có độ lớn động lượng lần lượt là $ { p _ 1 }=6kg.m/s $ và $ { p _ 2 }=4kg.m/s $ . Biết vận tốc của hai vật có hướng vuông góc với nhau. Độ lớn động lượng của hệ là:
- A
- B
- C
- D
Động lượng của hệ là: $ \overrightarrow p =\overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }} $
$ \overrightarrow{{ v _ 1 }}\bot \overrightarrow{{ v _ 2 }}\Rightarrow \overrightarrow{{ p _ 1 }}\bot \overrightarrow{{ p _ 2 }}\Rightarrow p=\sqrt{p_ 1 ^ 2 +p_ 2 ^ 2 }=\sqrt{{ 6 ^ 2 }+{ 4 ^ 2 }}=7,2(kg.m/s) $
Câu 82: Chọn câu phát biểu sai:
- A
- B
- C
- D
Sách giáo khoa VL 10, trang 124, mục II.1. Hệ cô lập: "Một hệ nhiều vật được gọi là cô lập (hệ kín) khi không có ngoại lực tác dụng lên hệ hoặc nếu có thì các ngoại lực ấy cân bằng nhau".
Câu 83: Một hệ gồm hai vật: vật thứ nhất có khối lượng $ { m _ 1 } $ , chuyển động với vận tốc $ { v _ 1 }=3m/s $ , vật thứ hai có khối lượng $ { m _ 2 }=1kg $ chuyển động với vận tốc $ { v _ 2 }=8m/s $ ngược hướng với hướng chuyển động của vật thứ nhất. Động lượng của hệ có độ lớn là 2 kg.m/s. Giá trị của $ { m _ 1 } $ là
- A
- B
- C
- D
Động lượng của vật 1 có độ lớn là: $ { p _ 1 }={ m _ 1 }{ v _ 1 }=3{ m _ 1 }\left( kg.m/s \right) $
Động lượng của vật 2 có độ lớn là: $ { p _ 2 }={ m _ 2 }{ v _ 2 }=1.8=8\left( kg.m/s \right) $
Động lượng của hệ 2 vật là: $ \overrightarrow p =\overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }} $
$ \begin{array}{l} & \overrightarrow{{ v _ 1 }}\uparrow \downarrow \overrightarrow{{ v _ 2 }}\Rightarrow \overrightarrow{{ p _ 1 }}\uparrow \downarrow \overrightarrow{{ p _ 2 }}\Rightarrow p=\left| { p _ 1 }-{ p _ 2 } \right|=\left| 3{ m _ 1 }-8 \right|=2 \\ & \Leftrightarrow {{\left( 3{ m _ 1 }-8 \right)}^ 2 }={ 2 ^ 2 }\Leftrightarrow 9m_ 1 ^ 2 -48{ m _ 1 }+64={ 2 ^ 2 } \\ & 9m_ 1 ^ 2 -48{ m _ 1 }+60=0\Rightarrow \left[ \begin{array}{l} & { m _ 1 }=2\left( kg \right) \\ & { m _ 1 }=\dfrac{10} 3 \left( kg \right) \\ \end{array} \right. \\ \end{array} $
Câu 84: Một tàu ngầm từ độ sâu 500 m dưới đáy biển chuyển động đều theo phương hợp với phương ngang một góc $ {{30}^ 0 } $ để nổi lên mặt nước. Khối lượng của tàu là 1500 tấn. Thành phần động lượng theo phương ngang của tàu là $ {{130.10}^ 5 }kgm{ s ^{-1}} $ . Thời gian tàu nổi lên đến mặt nước là:
- A
- B
- C
- D

Thành phần động lượng theo phương ngang là: $ { p _ X }={{130.10}^ 5 }kgm{ s ^{-1}} $
Thành phần động lượng theo phương thẳng đứng là: $ { p _ Y }={ p _ X }.\tan \alpha \Leftrightarrow m{ v _ y }={ p _ X }.\tan \alpha \Rightarrow { v _ y }=\dfrac{{ p _ X }.\tan \alpha } m $
Thời gian tàu nổi lên đến mặt nước là: $ t=\dfrac{h}{{}{ v _ y }}=\dfrac{mh}{{ p _ X }.\tan \alpha }=\dfrac{{{1500.10}^ 3 }.500}{{{130.10}^ 5 }.\tan {{30}^ 0 }}=100\left( s \right) $
Câu 85: Khi khối lượng vật giảm 2 lần thì động lượng.
- A
- B
- C
- D
Động lượng tỉ lệ với khối lượng của vật nên khi khối lượng giảm 2 lần thì động lượng cũng giảm 2 lần.
Câu 86: Khi vận tốc của một vật tăng gấp đôi thì
- A
- B
- C
- D
Biểu thức động lượng. p = m. v
Động lượng tỉ lệ với vận tốc nên khi vận tốc tăng gấp đôi thì động lượng cũng tăng gấp đôi.
Câu 87: Đơn vị của động lượng là
- A
- B
- C
- D
Biểu thức biến thiên động lượng \[ \Delta p=F.\Delta t\,\,(N.s) \]
Câu 88: Điều nào sau đây là không đúng khi nói về động lượng?
- A
- B
- C
- D
Đơn vị của động lượng là kg. m/s
Câu 89: Một vật khối lượng 1 kg chuyển động tròn đều với tốc độ 10 m/s. Độ biến thiên động lượng của vật sau 1/2 chu kì kể từ lúc bắt đầu chuyển động bằng
- A
- B
- C
- D

Vật chuyển động tròn đều nên động lượng của vật không đổi: p = mv = 1.10 = 10 (kg.m/s)
Biến thiên động lượng của vật là: $ \Delta \overrightarrow p =\overrightarrow{{ p _ 2 }}-\overrightarrow{{ p _ 1 }} $
Khi chất điểm chuyển động trên đường tròn thì vectơ vận tốc tại mỗi vị trí có phương tiếp tuyến với quỹ đạo.
Sau 1/2 chu kì kể từ lúc bắt đầu chuyển động thì góc quay của bán kính là $ \pi $
Nên $ \overrightarrow{{ v _ 1 }}\uparrow \downarrow \overrightarrow{{ v _ 2 }}\Rightarrow \overrightarrow{{ p _ 1 }}\uparrow \downarrow \bot \overrightarrow{{ p _ 2 }}\Rightarrow \Delta p={ p _ 1 }+{ p _ 2 }=2p=20\left( kg.m/s \right) $
Câu 90: Chọn câu phát biểu đúng nhất :
- A
- B
- C
- D
Sách giáo khoa VL 10, trang 125: "Động lượng của một hệ cô lập là một đại lượng bảo toàn".
Động lượng là một đại lượng vectơ nên phát biểu đúng nhất là: "Véc tơ động lượng toàn phần của hệ kín được bảo toàn"
Câu 91: Phát biểu nào sau đây SAI.
- A
- B
- C
- D
Động lượng của vật trong chuyển động tròn đều không đổi về độ lớn, nhưng hướng đổi liên tục.
Câu 92: Trường hợp nào vật có độ lớn động lượng không thay đổi?
- A
- B
- C
- D
Khi chuyển động tròn đều, độ lớn vận tốc không đổi nên độ lớn động lượng cũng không đổi.
Câu 93: Một đoàn tàu khối lượng 50 tấn đang chạy với vận tốc 54 km/h thì hãm phanh. Sau đó đi thêm 125 m nữa thì dừng hẳn. Hỏi 5 s sau lúc hãm phanh, động lượng của đoàn tàu là
- A
- B
- C
- D
v = 54 km/h = 15 m/s.
Từ biểu thức: $ { v ^ 2 }-v_ 0 ^ 2 =2\text{as}\Rightarrow 0-{{15}^ 2 }=2\text a \text{.125}\Rightarrow a=-0,9\left( m/{ s ^ 2 } \right) $
Vận tốc của vật sau 5s kể từ khi hãm phanh là: $ v={ v _ 0 }+at=15-0,9.5=10,5\left( m/s \right) $
Động lượng của vật sau 5s kể từ khi hãm phanh là: $ p=mv=50000.10,5=52,{{5.10}^ 4 }\left( kg.m/s \right) $
Câu 94: Chọn phát biểu đúng. Động lượng của một hệ cô lập là một đại lượng:
Động lượng của một hệ cô lập là một đại lượng:
- A
- B
- C
- D
Sách giáo khoa VL 10, trang 125: "Động lượng của một hệ cô lập là một đại lượng bảo toàn".
Câu 95: Trong quá trình nào sau đây, động lượng của ôtô không thay đổi
- A
- B
- C
- D
Biểu thức động lượng: $ \overrightarrow p =m\overrightarrow v $
Ôtô chuyển động thẳng đều trên đoạn đường có ma sát có vận tốc không thay đổi cả về hướng và độ lớn nên động lượng của ô tô trong trường hợp này không thay đổi
Câu 96: Một chiếc ô tô tải và một chiếc ô tô con có khối lượng lần lượt là 4 tấn và 1,5 tấn, chuyển động với các tốc độ 36km/h và 20m/s. Tỉ số động lượng của ô tô con so với ô tô tải là:
- A
- B
- C
- D
36km/h = 10 m/s
$ \left\{ \begin{array}{l} & { p _ 1 }={ m _ 1 }{ v _ 1 } \\ & { p _ 2 }={ m _ 2 }{ v _ 2 } \\ \end{array} \right.\Rightarrow \dfrac{{ p _ 2 }}{{ p _ 1 }}=\dfrac{{ m _ 2 }{ v _ 2 }}{{ m _ 1 }{ v _ 1 }}=\dfrac{1,5.20}{4.10}=\dfrac{3}{4} $
Câu 97: Trái đất có khối lượng $ 5,{{98.10}^{24}}kg $ chuyển động trên quỹ đạo tròn quanh Mặt trời với tốc độ $ 2,{{98.10}^ 4 }m/s $ . Động lượng của Trái đất là:
- A
- B
- C
- D
Động lượng của trái đất là: $ p=mv=5,{{98.10}^{24}}.2,{{98.10}^ 4 }=17,{{82.10}^{28}}\left( kg.m/s \right)=1,{{782.10}^{29}}\left( kg.m/s \right) $
Câu 98: Một vật nhỏ khối lượng m =2 kg trượt xuống một đường dốc thẳng nhẳn tại một thời điểm xác định có vận tốc 3m/s, sau đó 4s có vận tốc 7m/s, tiếp ngay sau đó 3s vật có động lượng (kgm/s) là
- A
- B
- C
- D
Chọn chiều dương là chiều chuyển động của vật.
Phương trình vận tốc của vật là: $ v={ v _ 0 }+at=3+at $ .
Ở thời điểm $ { t _ 1 }=4s $ thì v = 7 m/s, ta có: 7 = 3 + a.4 → a = 1 $ m/{ s ^ 2 } $ .
Ở thời điểm $ { t _ 2 }={ t _ 1 }+3=7\text s $ thì $ v=3+1.7=10\left( m/s \right) $
Động lượng: $ p=mv=2.10=20\left( kg.m/s \right) $
Xem thêm các bài tiếp theo bên dưới