Trong không gian với hệ trục tọa độ $\Large Oxyz$, cho các điểm $\Larg

Trong không gian với hệ trục tọa độ $\Large Oxyz$, cho các điểm $\Large A(1; 0; 1), B(1; -3; -5), C(3; -4; -3)$ và mặt phẳng $\Large (P): 2x-y+2z+5=0$. Xét các đường thẳng $\Large \Delta$ qua $\Large A$ và tạo với đường thẳng $\Large BC$ một góc $\Large 45^{\circ}$. Gọi $\Large M$ là giao điểm của $\Large \Delta$ với $\Large (P)$. Khi $\Large BM$ lớn nhất, $\Large \Delta$ có một véc-tơ chỉ phương là $\Large \overrightarrow{u_{\Delta}}=(1; a; b)$. Giá trị của $\Large a^2+b^2$ bằng

• A.

  1.

• B.

  2.

• C.

  10.

• D.

  5.

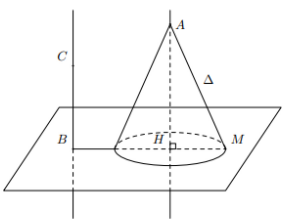
Ta có $\Large \overrightarrow{BC}=(2; -1; 2)$.

Mặt phẳng $\Large (P)$ có véc-tơ pháp tuyến $\Large \overrightarrow{n_(P)}=(2; -1; 2)=\overrightarrow{BC}$.

Suy ra $\Large BC\perp (P)$.

Gọi $\Large d$ là đường thẳng đi qua $\Large A$ và vuông góc mặt phẳng $\Large (P)$.

Khi đó $\Large d||BC$ suy ra $\Large d: \left\{\begin{align} & x=1+2t\\ & y=-t\\ & z=1+2t \end{align}\right.$

Gọi $\Large H=d\cap (P)\Rightarrow H(1+2t; -t; 1+2t)$.

Mà $\Large H\in (P)\Rightarrow 2(1+2t)-(-t)+2(1+2t)+5=0$ $\Large \Leftrightarrow t=-1\Rightarrow H(-1; 1; -1)$ và $\Large AH=3$.

Ta có $\Large \left(\widehat{\Delta, d}\right)=\left(\Delta, {d}'\right)=\widehat{HAM}=45^{\circ}$

Xét tam giác $\Large AHM$ vuông tại $\Large H$ có $\Large MH=AH.\tan 45^{\circ}=3$.

Suy ra $\Large M$ nằm trên đường tròn tâm $\Large H$ bán kính $\Large R=MH=3$.

Ta có $\Large BM$ lớn nhất khi $\Large B, H, M$ thẳng hàng và $\Large H$ ở giữa $\Large B, M$.

Suy ra $\Large IM$ đạt lớn nhất khi $\Large BM=BH+HM=\sqrt{(-1-1)^2+(1+3)^2+(-1+5)^2}+3=9$.

Ta lại có $\Large 2BM=3BH\Rightarrow 2\overrightarrow{BM}=3\overrightarrow{BH}$ $\Large \Leftrightarrow \left\{\begin{align} & 2(x_M-1)=3.(-2)\\ & 2(y_M+3)=3.4\\ & 2(z_M+5)=3.4 \end{align}\right.$ $\Large \Leftrightarrow \left\{\begin{align} & x_M=-2 \\ & y_M=3\\ & z_M=1 \end{align}\right.$

Suy ra $\Large M(-2; 3; 1)$ và véc-tơ chỉ phương $\Large \overrightarrow{u_{\Delta}}=\overrightarrow{MA}=(3; -3; 0)=3(1; -1; 0)$.

Vậy $\Large a=-1, b=0$ nên ta được $\Large a^2+b^2=1$.

Chọn đáp án A