Trong không gian tọa độ $\Large Oxyz$, cho hai mặt cầu $\Large (S_1):

Trong không gian tọa độ $\Large Oxyz$, cho hai mặt cầu $\Large (S_1): x^2+(y-1)^2+(z-2)^2=16$, $\Large (S_2): (x-1)^2+(y+1)^2+z^2=1$ và điểm $\Large A\left(\dfrac{4}{3}; \dfrac{7}{3}; -\dfrac{14}{3}\right)$. Gọi $\Large I$ là tâm của mặt cầu $\Large (S_1)$ và $\Large (P)$ là mặt phẳng tiếp xúc với cả hai mặt cầu $\Large (S_1)$ và $\Large (S_2)$. Xét các điểm $\Large M$ thay đổi và thuộc mặt phẳng $\Large (P)$ sao cho đường thẳng $\Large IM$ tiếp xúc với mặt cầu $\Large (S_2)$. Khi đoạn thẳng $\Large AM$ ngắn nhất thì $\Large M=(a; b; c)$. Tính giá trị của $\Large T=a+b+c$.

• A. $\Large T=1$.
• B. $\Large T=-1$.
• C. $\Large T=\dfrac{7}{3}$.
• D. $\Large T=-\dfrac{7}{3}$.

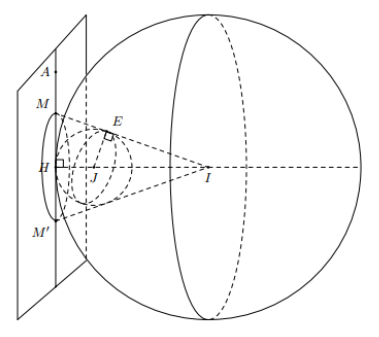
Ta có $\Large (S_1)$ có tâm là $\Large I(0; 1; 2)$ và bán kính là $\Large R_1=4$.

Và $\Large (S_2)$ có tâm là $\Large J(1; -1; 0)$ và bán kính là $\Large R_2=1$.

Ta lại có $\Large \overrightarrow{IJ}=(1; -2; -2)\Rightarrow IJ=3=R_1-R_2$ nên hai mặt cầu $\Large (S_1), (S_2)$ tiếp xúc trong.

Gọi $\Large H$ là tiếp điểm thì $\Large (P)$ là mặt phẳng qua $\Large H$ và nhận $\Large \overrightarrow{IJ}(-1; 2; 2)$ làm véc-tơ pháp tuyến.

Từ quan hệ $\Large \overrightarrow{IH}=4.\overrightarrow{JH}$ tìm được $\Large H=\left(\dfrac{4}{3}; -\dfrac{5}{3}; -\dfrac{2}{3}\right)$.

Suy ra $\Large (P): x-2y-2z-6=0$.

Nhận xét $\Large A\in (P)$ và $\Large \overrightarrow{HA}=(0; 4; -4)$, $\Large HA=4\sqrt{2}$.

Tập hợp các điểm $\Large M$ thỏa mãn $\Large IM$ tiếp xúc với mặt cầu $\Large (S_2)$ là một đường tròn nằm trong mp $\Large (P)$, đường tròn này có tâm $\Large H$ và bán kính là $\Large HM=\dfrac{JE}{EI}.HI=\dfrac{1}{\sqrt{3^2-1^2}}.4=\sqrt{2}$.

Ta có $\Large A$ nằm ngoài đường tròn này và $\Large AM$ đạt nhỏ nhất khi và chỉ khi $\Large M$ là giao điểm của đoạn thẳng $\Large HA$ và đường tròn.

Khi đó có $\Large \overrightarrow{HM}=\dfrac{\sqrt{2}}{HA}.\overrightarrow{HA}=\dfrac{1}{4}.\overrightarrow{HA}$ $\Large \Rightarrow M=\left(\dfrac{4}{3}; -\dfrac{2}{3}; -\dfrac{5}{3}\right)$ $\Large \Rightarrow a+b+c=-1$.

Chọn đáp án B