Quả cầu nhỏ khối lượng $\Large m$ mang điện tích $\Large +q$ trượt khô

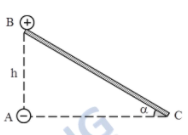
Quả cầu nhỏ khối lượng $\Large m$ mang điện tích $\Large +q$ trượt không ma sát với vận tốc $\Large v_0=0$ tại đỉnh B có độ cao $\Large h$ của mặt phẳng nghiêng BC. Tại đỉnh góc vuông A của tam giác ABC có một điện tích $\Large -q$. Giá trị nhỏ nhất của $\Large \alpha$ để quả cầu có thể tới được C là:

• A.

  $\Large tan \alpha_{min}=\dfrac{mgh^2}{kq^2}$.

• B.

  $\Large tan \alpha_{min}=1-\dfrac{mgh^2}{kq^2}$.

• C.

  $\Large tan \alpha_{min}=\dfrac{mgh}{kq}$.

• D.

  $\Large tan \alpha_{min}=1-\dfrac{mgh}{kq}$.

Chọn gốc thế năng ở chân mặt phẳng nghiêng; mốc thế năng điện ở vô cùng. Khi đó năng lượng của điện tích +q:

+ Tại B: $\Large E_B=\underset{E_d=0}{0}+mgh+\left(-\dfrac{kq^2}{h}\right)$.

+ Tại C: $\Large E_C=\dfrac{1}{2}mv^2+\underset{E_t=0}{0}+\left(-\dfrac{kq^2}{AC}\right)$ $\Large =\dfrac{1}{2}mv^2+\left(-\dfrac{kq^2tan\alpha}{h}\right)$.

Áp dụng bảo toàn cơ năng $\Large E_B=E_C$ $\Large \Rightarrow v=\sqrt{2\left[gh-(1-tan\alpha)\dfrac{kq^2}{mh}\right]}$.

Để quả cầu có thể C thì $\Large v\geq 0$ $\Large \Rightarrow tan\alpha \geq 1-\dfrac{mgh^2}{kq^2}$.

Đáp án B.