Một vật nhỏ đang dao động điều hoà với tần số góc là $\Large \omega=\p

Một vật nhỏ đang dao động điều hoà với tần số góc là $\Large \omega=\pi (rad/s)$. Tại thời điểm t = 0, vật nhỏ qua vị trí cân bằng theo chiều dương. Tại thời điểm nào thì vận tốc v và li độ x của vật nhỏ thoả mãn $\Large v=\omega x$ lần thứ 2019?

• A. A. 1009,25 s
• B. B. 2018,75 s
• C. C. 1008,75 s
• D. D. 2018,25 s

Chu kì dao động $\Large \dfrac{2\pi}{\omega}=\dfrac{2\pi}{\pi}=2s$

Ta có: $\Large v=\omega x \Leftrightarrow \omega\sqrt{A^2-x^2}=\omega x \Leftrightarrow A^2-x^2=x^2 \Leftrightarrow x=\pm \dfrac{A}{\sqrt{2}}$

Vì $\Large \omega >0$ nên v cùng dấu với x. Do đó, mỗi chu kì có 2 lần vật đi qua vị trí thoả mãn yêu cầu bài toán, đó là:

+ Vật đi qua vị trí $\Large x=\dfrac{A}{\sqrt{2}}$ theo chiều dương

+ Vật đi qua vị trí $\Large x=-\dfrac{A}{\sqrt{2}}$ theo chiều âm

Ta có hình vẽ

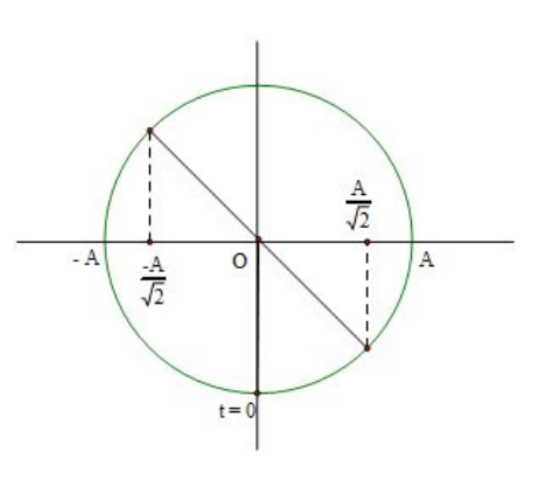
Thời gian để vật đi qua vị trí thoả mãn điều kiện bài toán lần thứ 2019 là:

$\Large t = 1009 T +\delta t$

Từ hình vẽ ta thấy $\Large \delta t = T/8$

Do đó, thay số vào ta tìm được t = 2018,25 s