Một mạch dao động điện từ lý tưởng đang dao động tự do. Tại thời điểm

Một mạch dao động điện từ lý tưởng đang dao động tự do. Tại thời điểm $\Large t = 0,$ điện tích trên một bản tụ điện cực đại. Sau khoảng thời gian ngắn nhất $\Large 10^{-6} s$ thì điện tích trên bản tụ này bằng nửa giá trị cực đại. Chu kì dao động riêng của mạch dao động này là 

• A.

  $\Large 12.10^{-6}s.$

• B.

  $\Large 6.10^{-6}s.$

• C.

  $\Large 4.10^{-6}s.$

• D.

  $\Large 3.10^{-6}s.$

Phương pháp: 
Sử dụng vòng tròn lượng giác và công thức: $\Large \Delta \varphi=\dfrac{2\pi}{T}.\Delta t$
Cách giải: 
Ta có vòng tròn lượng giác: 

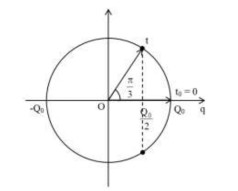
Từ vòng tròn lượng giác, ta thấy ở thời điểm đầu tiên điện tích trên bản tụ bằng nửa giá trị cực đại, vecto quay được góc: $\Large \Delta \varphi=\dfrac{\pi}{3} (rad) \Rightarrow \dfrac{\pi}{3}=\dfrac{2\pi}{T}.10^{-6} \Rightarrow T=6.10^{-6} (s)$  
Chọn B.