Một con lắc đơn gồm vật có khối lượng m, dây treo có chiều dài $\large

Một con lắc đơn gồm vật có khối lượng m, dây treo có chiều dài $\large l=2m$, lấy $\large g=\pi^2 (m/s^2)$.  Con lắc dao động điều hòa dưới tác dụng của ngoại lực có biểu thức $\large F=F_0.\cos\left(\omega t+\dfrac{\pi}{2}\right) (N)$. Nếu chu kì của ngoại lực tăng từ 4s lên 8s thì biên độ dao động cưỡng bức của vật sẽ .

• A. A. luôn tăng
• B. B. giảm rồi tăng.
• C. C. luôn giảm
• D. D. tăng rồi giảm

Phương pháp: 
+ Vận dụng lí thuyết về dao động cưỡng bức 
+ Cộng hưởng dao động 
Cách giải: 
+ Tần số cộng hưởng dao động:  $\large f_0=\dfrac{1}{2\pi}\sqrt{\dfrac{g}{l}}=\dfrac{1}{2\sqrt{2}} (Hz)=0,354 Hz$
+ Khi chu kì tăng từ 4s lên 8s tương ứng với tần số giảm từ $\large f_1=0,25 Hz$ đến $\large f_2=0,125 Hz$  
Ta có đồ thị:

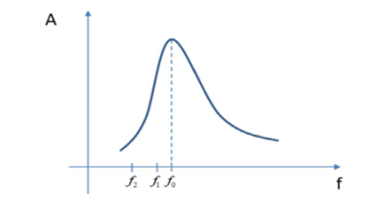
Từ đồ thị, ta thấy khi chu kì tăng từ 4s lên 8s thì biên độ dao động cưỡng bức luôn giảm. 
Chọn C.