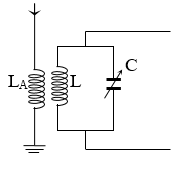
Mạch chọn sóng của một máy thu vô tuyến gồm một cuộn dây và một tụ xoa

Mạch chọn sóng của một máy thu vô tuyến gồm một cuộn dây và một tụ xoay. Điện trở thuần của mạch là R (R có giá trị rất nhỏ). Điều chỉnh điện dung của tụ điện đến giá trị ${{C}_{o}}$ để bắt được sóng điện từ có tần số góc $\omega $. Sau đó xoay tụ một góc nhỏ để suất điện động cảm ứng có giá trị hiệu dụng không đổi nhưng cường độ hiệu dụng của dòng điện trong mạch thì giảm xuống n lần. Hỏi điện dung của tụ thay đổi một lượng bao nhiêu?

• A. 2nR$\omega$$C_o$.
• B. nR$\omega$${{C}_{o}}^{2}$
• C. 2nR$\omega$${{C}_{o}}^{2}$ .
• D. nR$\omega$${C}_{o}$ .

Giải:  Để bắt được sóng điện từ tần số góc $\omega$, cần phải điều chỉnh tụ điện C đến giá trị $C_o$ thì trong mạch dao động điện từ có hiện tượng cộng hưởng: $Z_L$ = $Z_CO$ $\to$ $\omega$ L = $\large\dfrac{1}{\omega {{C}_{0}}}$. Suất điện động xuất hiện trong  mạch có giá trị hiệu dụng E$\to$  I = $\frac{\text{E}}{R}$---> Khi C=${{C}_{o}}+\Delta C$$\to $

Tổng trở Z = $\sqrt{{{R}^{2}}+{{(\omega L-\dfrac{1}{\omega C})}^{2}}}$ tăng lên, (với $\delta$C độ biến dung của tụ điện)

Cường độ hiệu dụng trong mạch  I’ = $\large\dfrac{\text{E}}{Z}$-----> $\dfrac{\text{I}}{n}$ = $\dfrac{\text{E}}{Z}$ = $\dfrac{\text{E}}{\sqrt{{{R}^{2}}+{{(\omega L-\frac{1}{\omega C})}^{2}}}}$=$\large\dfrac{\text{E}}{nR}$ $\to$ $R^2$ + ${{(\omega L-\dfrac{1}{\omega C})}^{2}}={{n}^{2}}{{R}^{2}}$$\to$$\large({{n}^{2}}-1){{R}^{2}}={{\left( \dfrac{1}{\omega {{C}_{o}}}-\dfrac{1}{\omega C} \right)}^{2}}=\dfrac{1}{{{\omega }^{2}}}{{\left( \dfrac{1}{{{C}_{o}}}-\dfrac{1}{{{C}_{o}}+\Delta C} \right)}^{2}}\to \dfrac{1}{{{\omega }_{2}}}\dfrac{{{(\Delta C)}^{2}}}{{{C}_{o}}^{2}{{({{C}_{o}}+\Delta C)}^{2}}}={{n}^{2}}{{R}^{2}}-{{R}^{2}}$

Vì R rất nhỏ nên $\large{{R}^{2}}\approx 0$  và  tụ xoay một góc nhỏ nên   $C_o$ + $\delta C$ $\large\approx {{C}_{o}}$  $\frac{1}{\omega }$$\large\dfrac{\Delta \text{C}}{C_{0}^{2}}$= n R $\to \Delta C=nR\omega {{C}_{o}}^{2}$.