Hai điểm sáng A và B dao động điều hòa cùng tần số trên trục Ox với cù

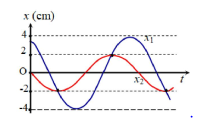
Hai điểm sáng A và B dao động điều hòa cùng tần số trên trục Ox với cùng vị trí cân bằng O. Hình bên là đồ thị li độ $\Large x _{1} \text { và } x _{2}$ của A và B phụ thuộc vào thời gian t. Trong quá trình dao động, khoảng cách xa nhất giữa hai điểm sáng là 

• A. $\Large 2 \sqrt{2} cm$
• B. $\Large 2 \sqrt{3} cm$
• C. $\Large 3\sqrt{3} cm$
• D. $\Large 3\sqrt{2} cm$

Phương pháp: 
Sử dụng kĩ năng đọc đồ thị để viết phương trình dao động 
Khoảng cách giữa hai vật: $\Large x = x _{1}- x _{2}= A \cos (\omega t +\varphi)$
Khoảng cách xa nhất giữa hai vật: $\Large x _{\max }= A$ 
Cách giải: 
Từ đồ thị, ta thấy hai dao động cùng tần số 
Ở thời điểm đầu, vật 2 có li độ $\Large x _{2}=0$ và đang giảm, ta có phương trình dao động:
$\Large x _{2}=2 \cos \left(\omega t +\dfrac{\pi}{2}\right)( cm )$ 
Vật 2 đến biên âm lần đầu tiên ở thời điểm $\Large t =\dfrac{ T }{4}$ khi đó vật 1 có li độ là $\Large x _{1}=-\dfrac{ A _{1}}{2}$
Ta có vòng tròn lượng giác cho vật 1:

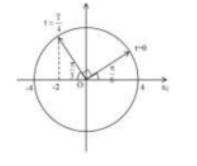
Từ vòng tròn lượng giác, ta thấy pha ban đầu của vật 1 là $\Large \varphi_{1}=\dfrac{\pi}{6}( rad )$
Phương trình li độ của vật 1 là: $\Large x _{1}=4 \cos \left(\omega t +\dfrac{\pi}{6}\right)$
Khoảng cách giữa hai vật là: 

$\Large \begin{array}{l}
x=x_{1}-x_{2}=4 \cos \left(\omega t+\dfrac{\pi}{6}\right)-2 \cos \left(\omega t+\dfrac{\pi}{2}\right) \\
\Rightarrow x=4 \cos \left(\omega t+\dfrac{\pi}{6}\right)+2 \cos \left(\omega t-\dfrac{\pi}{2}\right)
\end{array}$
Biên độ dao động tổng hợp là: 

$\Large A =\sqrt{ A _{1}^{2}+ A _{2}^{2}+2 A _{1} A _{2} \cos \left(\dfrac{\pi}{6}+\dfrac{\pi}{2}\right)}=2 \sqrt{3}( cm )$

Khoảng cách xa nhất giữa hai vật là $\Large A =2 \sqrt{3} cm$
Chọn B.