Giả sử $\Large z_1$, $\Large z_2$ là hai số phức thỏa mãn $\Large |z_1

Giả sử $\Large z_1$, $\Large z_2$ là hai số phức thỏa mãn $\Large |z_1-2-3i|=1$ và $\Large |z_2+2+5i|=2$ và số phức $\Large z$ thỏa mãn $\Large |z-3-i|=|z-1+i|$. Tìm giá trị nhỏ nhất của biểu thức $\Large T=|z-z_1|+|z-z_2|$.

• A. $\Large 4\sqrt{5}$.
• B. $\Large 2\sqrt{5}$.
• C. $\Large 4\sqrt{5}-3$.
• D. $\Large 2\sqrt{5}-1$.

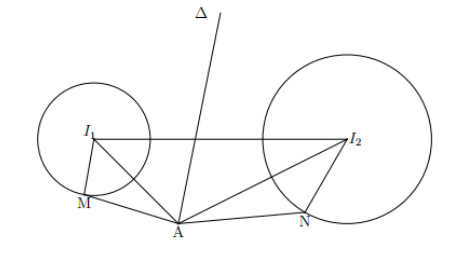
Gọi $\Large M(z_1)$, khi đó $\Large |z_1-2-3i|=1\Leftrightarrow M\in (C_1)$ với $\Large (C_1)$ là đường tròn $\Large I_1(2; 3)$ với $\Large R_1=1$.

Gọi $\Large N(z_2)$, khi đó $\Large |z_2+2+5i|=2\Leftrightarrow N\in (C_2)$ với $\Large (C_2)$ là đường tròn tâm $\Large I_2(-2; -5)$ và $\Large R_2=2$.

Gọi $\Large A(z)$ và $\Large z=x+yi$, khi đó

$\Large |z-3-i|=|z-1+i|\Leftrightarrow (x-3)^2+(y-1)^2=(x-1)^2+(y+1)^2\Leftrightarrow x+y-2=0$.

Suy ra $\Large A\in \Delta: x+y-2=0$. Ta có

$\Large T=AM+AN=(AM+MI_1)+(AN+NI_2)-3\geq AI_1+AI_2-3\geq I_1I_2-3=4\sqrt{5}-3$.

Dấu "=" xảy ra khi $\Large \begin{Bmatrix}
A
\end{Bmatrix}=I_1I_2\cap \Delta$. Vậy $\Large T_{\min}=4\sqrt{5}-3$.