Đặt điện áp $\Large u=U\sqrt{2}cos2\pi ft$ (U không đổi, f thay đổi đư

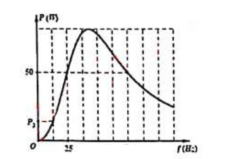
Đặt điện áp $\Large u=U\sqrt{2}cos2\pi ft$ (U không đổi, f thay đổi được) vào hai đầu đoạn mạch AB nối tiếp gồm điện trở R, cuộn cảm thuần L và tụ điện C. Khi $\Large f = 25 Hz$ thì u sớm pha hơn $\Large u_C$ là $\Large 60^{\circ}.$ Hình vẽ bên là đồ thị phụ thuộc f của công suất mạch tiêu thụ. Giá trị $\Large P_3$ gần giá trị nào nhất sau đây? 

• A. 10 W.
• B. 9,2 W.
• C. 6,5 W.
• D. 18 W.

Phương pháp: 
Sử dụng kĩ năng đọc đồ thị 
Công suất tiêu thụ: $\Large P=\dfrac{U^2R}{R^2+(Z_L-Z_C)^2}$
Độ lệch pha giữa cường độ dòng điện và hiệu điện thế giữa hai đầu đoạn mạch: $\Large cos\varphi=\dfrac{R}{\sqrt{R^2+(Z_L-Z_C)^2}}$
Cách giải: 
Từ đồ thị ta thấy 2 ô ứng với tần số 25 Hz $\Large \rightarrow$ 1 ô ứng với tần số 12,5 Hz 
Với $\Large f_1 = 25 Hz$ và $\Large f_2 = 75 Hz,$ công suất tiêu thụ trên mạch có cùng giá trị: 
$\Large P_1=P_2=\dfrac{U^2R}{R^2+(Z_L-Z_C)^2}=\dfrac{U^2R}{R^2+(Z_L-Z_C)^2}$
$\Large \Rightarrow (Z_{L_{1}}-Z_{C_1})^2=(Z_{L_2}-Z_{C_2})^2 $ 
Lại có: $\Large f_2=3f_1$ $\Large \Rightarrow \left\{\begin{align} & Z_{L_2}=3Z_{L_1} \\ & Z_{C_2}=\dfrac{1}{3}Z_{C_1} \end{align}\right.$
$\Large \Rightarrow (Z_{L_1}-Z_{C_1})^2=\left(3Z_{L_1}-\dfrac{1}{3}Z_{C_1}\right)^2$
$\Large \Rightarrow \left[\begin{align} & Z_{L_1}-Z_{C_1}=3Z_{L_1}-\dfrac{1}{3}Z_{C_1} \Rightarrow -2Z_{L_1}=\dfrac{2}{3}Z_{C_1} (loai) \\ & Z_{L_1}-Z_{C_1}=-3Z_{L_1}+\dfrac{1}{3}Z_{C_1} \Rightarrow 4Z_{L_1}=\dfrac{4}{3}Z_{C_1} \Rightarrow Z_{C_1}=3Z_{L_1}=3m (t/m)  \end{align}\right.$
Khi tần số $\Large f_1 = 25 Hz,$ độ lệch pha giữa cường độ dòng điện và điện áp giữa hai đầu đoạn mạch là: 
$\Large \varphi=\dfrac{\pi}{2}-\dfrac{\pi}{3}=\dfrac{\pi}{6}\Rightarrow cos\dfrac{\pi}{6}=\dfrac{R}{\sqrt{R^2+(m-3m)^2}}$
$\Large \Rightarrow \dfrac{\sqrt{3}}{2}=\dfrac{R}{\sqrt{R^2+4m^2}}\Rightarrow 3R^2+12m^2=4R^2 \Rightarrow R=2\sqrt{3}m$ 
Khi tần số $\Large f_3 = 12,5 (Hz) = 0,5f_1$ công suất tiêu thụ trên mạch là: 
$\Large \left\{\begin{align} & P_3=\dfrac{U^2.2\sqrt{3}m}{(2\sqrt{3}m)^2+(0,5m-6m)^2}=\dfrac{U^2.2\sqrt{3}m}{42,25m^2} \\ & P_1=\dfrac{U^2.2\sqrt{3}m}{(2\sqrt{3}m)^2+4m^2}=\dfrac{U^2.2\sqrt{3}m}{16m^2}=50 \end{align}\right.$
$\Large \Rightarrow \dfrac{P_3}{P_1}=\dfrac{16m^2}{42,25m^2}=\dfrac{16}{42,25} \Rightarrow P_3=\dfrac{16}{42,25}P_1=18,93 (W)$
Chọn D.