: Cho số phức z thỏa mãn $\large |z-2-3i|=1$. Giá trị lớn nhất của $\l

: Cho số phức z thỏa mãn $\large |z-2-3i|=1$. Giá trị lớn nhất của $\large |\bar{z}+1+i \mid$ là

• A.

  A. 4

• B.

  B. 6

• C.

  C. $\large \sqrt{13}+1$

• D.

  D. $\large \sqrt{13}+2$

Chọn C
Cách 1:
Gọi $\large z=x+y i$, với $\large x, y \in \mathbb{R}$
Ta có $\large z-2-3 i=x+y i-2-3 i=x-2+(y-3) i$.
Theo giả thiết $\large |z-2-3 i|=1 \Leftrightarrow(x-2)^{2}+(y-3)^{2}=1$ nên điểm M biểu diễn cho số phức z nằm trên đường tròn (C) tâm I(2;3), bán kính R=1

$\large |\bar{z}+1+i|=|x-y i+1+i|=|x+1+(1-y) i|=\sqrt{(x+1)^{2}+(y-1)^{2}}$
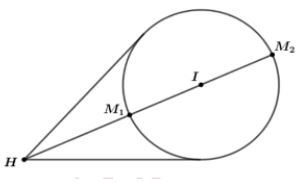
Gọi M(x;y) và H(-1;1) thì $\large H M=\sqrt{(x+1)^{2}+(y-1)^{2}}$
Do M chạy trên đường tròn (C), H cố định và H nằm ngoài đường tròn (C) nên MH lớn nhất khi M là giao của HI với đường tròn (C) sao cho I nằm giữa H và M.
Phương trình $\large H I:\left\{\begin{array}{l}
x=2+3 t \\
y=3+2 t
\end{array}\right.$
Giao của HI với đường tròn ứng với t thỏa mãn: $\large 9 t^{2}+4 t^{2}=1 \Leftrightarrow t=\pm \dfrac{1}{\sqrt{13}}$
Suy ra $\large M\left(2+\dfrac{3}{\sqrt{13}} ; 3+\dfrac{2}{\sqrt{13}}\right), M\left(2-\dfrac{3}{\sqrt{13}} ; 3-\dfrac{2}{\sqrt{13}}\right)$
Với $\large M\left(2+\dfrac{3}{\sqrt{13}} ; 3+\dfrac{2}{\sqrt{13}}\right)$, ta có $\large M H=\sqrt{13}+1$
Với $\large M\left(2-\dfrac{3}{\sqrt{13}} ; 3-\dfrac{2}{\sqrt{13}}\right)$, ta có $\large M H \approx 1,92$. Vậy GTLN của $\large |\bar{z}+1+t|=\sqrt{13}+1$.