Cho mạch điện xoay chiều nối tiếp R, C. Đặt vào hai đầu đoạn mạch một

Cho mạch điện xoay chiều nối tiếp R, C. Đặt vào hai đầu đoạn mạch một hiệu điện thế $\large u=120\sqrt{2}.\cos(100\pi t) (V)$  thì $\large Z_C=\dfrac{R}{\sqrt{3}}$. Tại thời điểm  $\large t=\dfrac{1}{150}s$ thì hiệu điện thế trên tụ có giá trị bằng 

• A. A.$\large 60\sqrt{2} V$
• B. B. $\large 60\sqrt{6} V$
• C. C. $\large 30\sqrt{2} V$
• D. D. $\large 30\sqrt{6} V$

Phương pháp: 
+ Sử dụng biểu thức tính điện áp giữa hai đầu đoạn mạch 
+ Sử dụng giản đồ pha 
+ Thay t vào phương trình điện áp 
Cách giải: 
Ta có: $\large Z_c=\dfrac{R}{\sqrt{3}}\Rightarrow U_{0C}=\dfrac{U_{OR}}{\sqrt{3}}$ (1)
Lại có: $\large U_0^2=U_{OR}^2+U_{OC}^2$ (2)  
Từ (1) và (2) suy ra: $\large \left\{\begin{align}& U_{OR}=60\sqrt{6} V\\& U_{OC}=60\sqrt{2} V\\\end{align}\right.$

 $\large tan\varphi =\frac{U_{C}}{U_{R}}=\frac{1}{\sqrt{3}}\Rightarrow \varphi =\dfrac{\pi }{6}$

Ta có giản đồ vecto: 

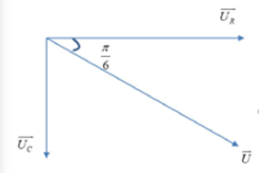
Phương trình điện áp giữa 2 đầu tụ điện: $\large u_C=60\sqrt{2}\cos \left(100\pi t-\dfrac{\pi}{3}\right) V$  
Tại $\large t=\dfrac{1}{150} s$ thì $\large u_C=60\sqrt{2}\cos\left( 100\pi. \dfrac{1}{150}-\dfrac{\pi}{3}\right)=30\sqrt{2} V$  
Chọn C.