Cho khối chóp S.ABCD có đáy là hình vuông cạnh a,SA
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho khối chóp S.ABCD có đáy là hình vuông cạnh a,SA vuông góc với đáy và SC tạo với mặt phẳng (SAB) một góc 30∘. Tính thể tích V của khối chóp đã cho.
Đáp án án đúng là: B
Lời giải chi tiết:
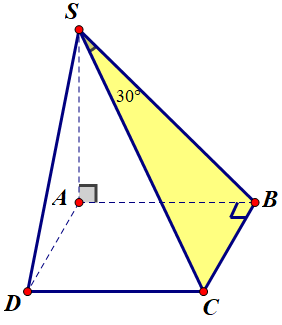
Do CB⊥(SAB), suy ra SB là hình chiếu vuông góc của SC lên (SAB)⇒(SC,(SAB))=^CSB=30∘
(có thể thấy góc giữa SC với (SAB) là góc tạo bởi cạnh bên và mặt đứng).
Ta có: SB=CB⋅cot30∘=a√3
⇒SA=√SB2−AB2=√(a√3)2−a2=a√2
Suy ra V=13SA.SABCD=13⋅a√2.a2=√2a33
Đáp án B
Xem thêm các bài tiếp theo bên dưới