Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC). Tam giác ABC

Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC). Tam giác ABC đều cạnh bằng $\large a\sqrt{ 3}$, tam giác SAC cân. Tính khoảng cách h từ A đến (SBC) .

• A. A. $\large h=\dfrac{3a}{\sqrt{7}}$
• B. B. $\large h=\dfrac{a\sqrt{3}}{4}$
• C. C. $\large h=\dfrac{a}{\sqrt{7}}$
• D. D. $\large h=\dfrac{a\sqrt{3}}{7}$

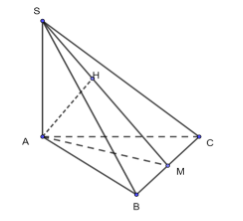
Gọi M là trung điểm của BC. Kẻ $\large AH\perp SM, (H\in SM)$ (1)

Ta có: $\large \left\{\begin{align}& BC\perp SA, ( SA\perp (ABC))\\& BC\perp AM, (\Delta ABC \text{ đều })\\\end{align}\right. $ $\large \Rightarrow BC\perp (SAM)\Rightarrow BC\perp AH$ (2)

Từ (1), (2) $\large AH\perp (SBC)\Rightarrow h=AH$

Vì $\large \Delta ABC$ đều cạnh $\large a\sqrt{3}\Rightarrow AM=\sqrt{3}.\dfrac{\sqrt{3}}{2}=\dfrac{3a}{2}$

Vì $\large \Delta SAC$ cân mà $\large SA\perp AC\Rightarrow SA=AC=a\sqrt{3}$

Xét $\large \Delta SAM$ vuông tại A ta có: $\large \dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AM^2}=\dfrac{1}{3a^2}+\dfrac{4}{9a^2}=\dfrac{7}{9a^2}\Rightarrow AH=\dfrac{3a}{\sqrt{7}}$

Vậy $\large h=\dfrac{3a}{\sqrt{7}}$