Cho hình chóp $\large S.ABC$ có đáy $\large ABC$ là tam giác vuông cân

Cho hình chóp $\large S.ABC$ có đáy $\large ABC$ là tam giác vuông cân tại $\large C,SA$ vuông góc với đáy, $\large SC=a$. Gọi $\large\alpha $ là góc giữa hai mặt phẳng $\large (SBC)$ và $\large (ABC)$. Tính $\large\sin \alpha $ để thể tích khối chóp $\large S.ABC$ lớn nhất

• A.

  A. $\large\sin \alpha =\dfrac{\sqrt{3}}{4}$

• B.

  B. $\large\sin \alpha =\dfrac{\sqrt{3}}{6}$

• C.

  C. $\large\sin \alpha =\dfrac{2}{3 \sqrt{3}}$

• D.

  D. $\large\sin \alpha =\dfrac{1}{\sqrt{3}}$

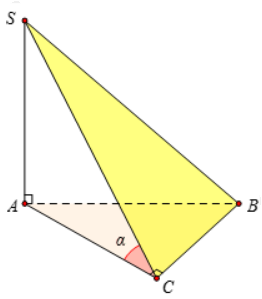
Do $\large SA\perp (ABC)\Rightarrow((SBC),(ABC))=\widehat{SCA}=\alpha $

Trong tam giác vuông $\large SAC$ có 

$\large\left\{\begin{align}BC=AC=SC\cos \alpha =a\cos \alpha \\ SA=SC\sin \alpha =a\sin \alpha\end{align}\right.$

Khi đó thể tích khối chóp $\large S.ABC$ là $\large V=\dfrac{1}{3} SA\cdot  S_{ABC}=\dfrac{1}{6}.a^{3}\cos ^{2}\alpha.\sin \alpha$

Theo bất đẳng thức $\large AM-GM$ (Cauchy) ta có:

$\large V^{2}=\dfrac{1}{36}a^{6}\cdot \cos ^{4}\alpha \cdot \sin ^{2}\alpha =\dfrac{1}{36}a^{6}\left(1-\sin ^{2}\alpha\right)^{2}\cdot \sin ^{2} \alpha$

$\large =\dfrac{4a^{6}}{36}\cdot \dfrac{1-\sin ^{2} \alpha}{2} \dfrac{1-\sin ^{2} \alpha}{2} \sin ^{2} \alpha \leq \dfrac{4a^{6}}{36}.\left(\dfrac{\dfrac{1-\sin ^{2}\alpha}{2}+\dfrac{1-\sin ^{2} \alpha}{2}+\sin ^{2} \alpha}{3}\right)^{3}=\dfrac{a^{6}}{243}\Rightarrow V \leq \dfrac{a^{3} \sqrt{3}}{27}$

Dấu "=" xảy ra khi $\large\dfrac{1-\sin ^{2} \alpha}{2}=\sin ^{2}\alpha \Leftrightarrow \sin \alpha=\dfrac{1}{\sqrt{3}}$

Đáp án D