Cho hình chóp đều S.ABC có $\Large \widehat{A S B}=30^{\circ}$. Một mặ

Cho hình chóp đều S.ABC có $\Large \widehat{A S B}=30^{\circ}$. Một mặt phẳng thay đổi qua A cắt SB, SC tại M, N. Tính tỷ số thể tích của khối chóp S.AMN và khối chóp S.ABC khi chu vi tam giác AMN đạt giá trị nhỏ nhất. 

• A.

  $\Large 2(\sqrt{3}-1)$

• B.

  $\Large \dfrac{3+\sqrt{2}}{5}$

• C.

  $\Large \dfrac{2(\sqrt{3}-1)}{4}$

• D.

  $\Large 2(2-\sqrt{3})$

Chọn D

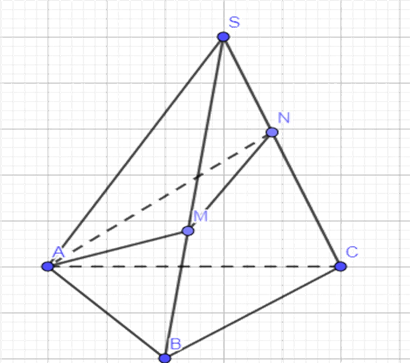
Cắt tứ diện theo cạnh SA sau đó trải trên mặt phẳng (SBC)

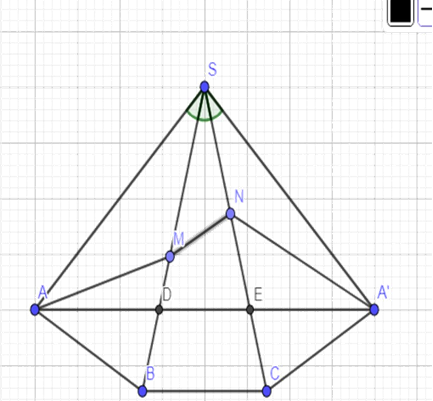
Ta có chu vi tam giác $\Large C_{A M N}=A M+M N+A N=AM + MN + NA' \geq AA'$

Đặt $\Large S A=a$ ta có $\Large A A^{\prime 2}=S A^{2}+S A'^{2}-2 S A S A' \cos 90^{\circ}=2 a^{2} \Rightarrow A A'=a \sqrt{2}$

Dấu bằng khi $\Large A, M, N, A'$ thẳng hàng

Xét tam giác SAE có $\Large \hat{S}=30^{0}, \widehat{S A E}=45^{0}$ vì tam giác SAE' cân tại S

Suy ra $\Large \widehat{S E A}=105^{\circ}$ vậy $\Large \dfrac{S E}{\sin 45^{0}}=\dfrac{S A}{\sin 105^{0}} \Rightarrow \dfrac{S E}{S A}=\dfrac{\sin 45^{0}}{\sin 105^{0}}$

Tương tự trong tam giác SA'F có $\Large \dfrac{S F}{S A^{\prime}}=\dfrac{\sin 45^{0}}{\sin 105^{0}}$

Vậy $\Large \dfrac{V_{S A M N}}{V_{S A B C}}=\dfrac{S E}{S B} \cdot \dfrac{S F}{S C}=\dfrac{S E}{S A} \cdot \dfrac{S F}{S A'}=\left(\dfrac{\sin 45^{\circ}}{\sin 105^{\circ}}\right)^{2}=2(2-\sqrt{3})\left(S A=S B=S C=S A^{\prime}\right)$