Cho hàm số $\Large y=f(x)=ax^3+bx^2+cx+d (a; b; c; d \in \mathbb{R})$

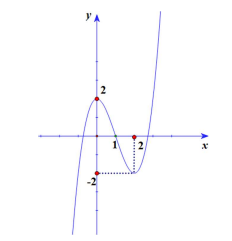
Cho hàm số $\Large y=f(x)=ax^3+bx^2+cx+d  (a; b; c; d \in \mathbb{R})$ có đồ thị như hình vẽ bên. Số nghiệm của phương trình $\Large 4f(x)+3=0$ là

• A. 3.
• B. 0.
• C. 1.
• D. 2.

Chọn A

Số nghiệm của phương trình $\Large 4f(x)+3=0 \Leftrightarrow f(x)=-\dfrac{3}{4}$ chính là số giao điểm của đồ thị hàm số $\Large f(x)$ và đường thẳng $\Large y=-\dfrac{3}{4}.$

Quan sát đồ thị hàm số ta thấy đồ thị hàm số $\Large f(x)$ cắt đường thẳng $\Large y=-\dfrac{3}{4}$ tại 3 điểm phân biệt.

Vậy phương trình $\Large 4f(x)+3=0$ có ba nghiệm.