Cho hàm số $\Large y=f(x)$ liên tục trên $\Large \mathbb{R}$ và có đồ

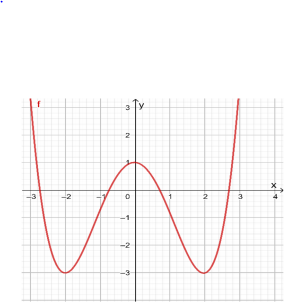
Cho hàm số $\Large y=f(x)$ liên tục trên $\Large \mathbb{R}$ và có đồ thị như hình vẽ bên dưới.

Số nghiệm của phương trình $\Large 2f(x)+1=0$.

• A. 1.
• B. 2.
• C. 3.
• D. 4.

Chọn D

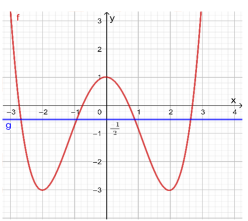
Ta có $\Large 2f(x)+1=0$ $\Large \Leftrightarrow f(x)=\dfrac{-1}{2}$ (*). Ta có số nghiệm của phương trình (*) chính là số giao điểm của đồ thị hàm số $\Large y=f(x)$ và $\Large y=-\dfrac{1}{2}$. Vẽ đồ thị hàm số $\Large y=-\dfrac{1}{2}$ và $\Large y=f(x)$ trên cùng 1 hệ trục tọa độ ta được như sau. Từ đó ta thấy đường thẳng $\Large y=-\dfrac{1}{2}$ cắt đồ thị hàm số $\Large y=f(x)$ tại 4 điểm phân biệt.

Vậy phương trình (*) có 4 nghiệm phân biệt.