Cho hai hàm số $\large y=f(x), y=g(x)$ có đồ thị của hàm số $\large y=

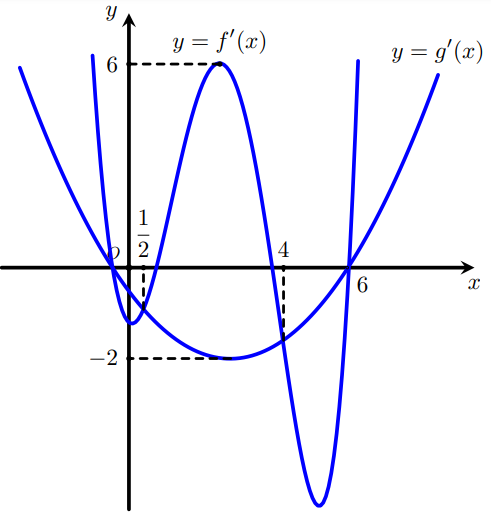
Cho hai hàm số $\large y=f(x), y=g(x)$ có đồ thị của hàm số $\large y=f^{\prime}(x), y=g^{\prime}(x)$ như hình vẽ bên. Hàm số $\large y=f\left(2 x+\frac{1}{2}\right)-g(3 x+6)-18 x$ nghịch biến trên khoảng nào dưới đây?

• A.

  A. $\large \left(-\infty ;-\dfrac{1}{4}\right)$

• B.

  B. $\large \left(\dfrac{11}{4} ;+\infty\right)$

• C.

  C. $\large \left(-2 ; \dfrac{5}{4}\right)$

• D.

  D. $\large \left(-\dfrac{1}{4} ; \dfrac{11}{4}\right)$

Ta có $\Large y^{\prime}=2 f^{\prime}\left(2 x+\dfrac{1}{2}\right)-3 g^{\prime}(3 x+6)-18$

Xét đáp án D.

$\Large -\dfrac{1}{4} < x < \dfrac{11}{4} \Leftrightarrow 0 < 2 x+\dfrac{1}{2} < 6 \Rightarrow f^{\prime}\left(2 x+\dfrac{1}{2}\right) < 6 \Leftrightarrow 2 f^{\prime}\left(2 x+\dfrac{1}{2}\right) < 12$

$\Large -\dfrac{1}{4} < x < \dfrac{11}{4} \Leftrightarrow 5,25 < 3 x+6 < 14,25 \Rightarrow g^{\prime}(3 x+6) > -2 \Leftrightarrow-3 g^{\prime}(3 x+6) < 6$

Suy ra $\Large 2 f^{\prime}\left(2 x+\dfrac{1}{2}\right)-3 g^{\prime}(3 x+6) < 12+6=18$ $\Large \Leftrightarrow y^{\prime}=2 f^{\prime}\left(2 x+\dfrac{1}{2}\right)-3 g^{\prime}(3 x+6)-18 < 0$

Vậy hàm số nghịch biến trên $\Large \left(-\dfrac{1}{4} ; \dfrac{11}{4}\right)$