Cho hai dao động điều hòa cùng phương với các phương trình dao động lầ

MỤC LỤC
Câu hỏi:
Cho hai dao động điều hòa cùng phương với các phương trình dao động lần lượt là $\Large \text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }{{\text{x}}_{1}}={{\text{A}}_{1}}\text{cos}\left( \text{ }\!\!\omega\!\!\text{ t}+\dfrac{\text{ }\!\!\pi\!\!\text{ }}{2} \right)$(cm) và $\Large {{\text{x}}_{2}}={{\text{A}}_{2}}\text{cos}\left( \text{ }\!\!\omega\!\!\text{ t}+\text{ }\!\!~\!\!\text{ }\dfrac{\text{ }\!\!\pi\!\!\text{ }}{6} \right)$(cm). Dao động tổng hợp của hai dao động này có phương trình là $\Large x=\text{ }30cos(\omega t+\varphi )\text{ }\left( cm \right).$. Giá trị cực đại của ($\Large {{\text{A}}_{1}}+\text{ }\!\!~\!\!\text{ }{{\text{A}}_{2}}$) gần nhất với giá trị nào sau đây
Đáp án án đúng là: D
Lời giải chi tiết:
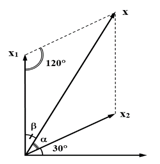
Từ hình vẽ ta có: $\Large \dfrac{A}{\sin 120{}^\circ }=\dfrac{{{A}_{1}}}{\sin \alpha }=\dfrac{{{A}_{2}}}{\sin \beta }=\dfrac{{{A}_{1}}+{{A}_{2}}}{\sin \alpha +\sin \beta }=\dfrac{{{A}_{1}}+{{A}_{2}}}{2\sin \dfrac{\alpha +\beta }{2}\cos \dfrac{\alpha -\beta }{2}}.$
Suy ra $\Large {{A}_{1}}+{{A}_{2}}=\dfrac{2A\sin \dfrac{180-120}{2}\sin \dfrac{\alpha -\beta }{2}}{\sin 120{}^\circ } \dfrac{2A\sin 30{}^\circ }{\sin 120{}^\circ }\approx 35 cm.$
Xem thêm các bài tiếp theo bên dưới
- Treo một vật vào đầu dưới của lò xo có đầu trên được giữ cố định. Khi
- Con lắc lò xo được treo thẳng đứng tại vị trí cân bằng lò xo dãn $\Lar
- Một con lắc lò xo gồm vật nặng có khối lượng 300g gắn vào lò xo. Đồ th
- Vận tốc của chất điểm dao động điều hòa có độ lớn cực đại khi nào? A.
- Một vật dao động điều hòa với phương trình: $\Large x=5\cos (\pi t-\df