Tập hợp tất cả các số thực của tham số m để phương trình $\large x^6 +

Tập hợp tất cả các số thực của tham số m để phương trình $\large x^6 + 6x^4 - m^3x^3 + (15- 3m^2)x^2-6mx + 10=0$ có đúng hai nghiệm phân biệt thuộc đoạn $\large \left[\dfrac{1}{2}; 2\right] $ là: 

• A. $\large 2 < m \leq \dfrac{5}{2}$
• B. $\large \dfrac{7}{5}\leq m < 3$
• C. $\large \dfrac{11}{5} < m < 4$
• D. $\large 0 < m < \dfrac{9}{4}$

Chọn A

Ta có: 

$\large x^6 + 6x^4 - m^3x^3 + (15- 3m^2)x^2-6mx + 10=0$

$\large \Leftrightarrow (x^2+ 2)^3+3(x^2+2)= (mx+1)^3+ 3(mx+1)$

$\large \Leftrightarrow f(x^2+2)= f(mx+1)\, (*)$

Với $\large f(t) = t^3+3t$. Do: $\large f'(t) = 3t^2+ 3 > 0, \forall t \in \mathbb{R}$

Hàm số f(t) đồng biến trên $\large \mathbb{R}$. Nên $\large (*) \Leftrightarrow x^2 + 2 = mx + 1$

$\large \Leftrightarrow x^2 - mx+ 1= 0\Leftrightarrow m =\dfrac{x^2+1}{x}$

Xét hàm số $\large g(x) = \dfrac{x^2+1}{x}$ trên $\large \left[\dfrac{1}{2}; 2\right]$

Ta có: $\large g'(x) = 1- \dfrac{1}{x^2} \Rightarrow g'(x) = 0\Leftrightarrow x =1 $

Bảng biến thiên: 

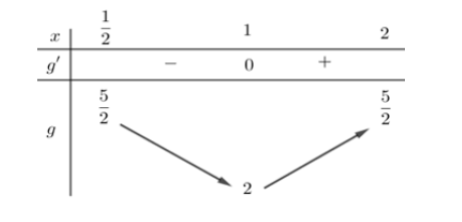
Dựa vào bảng biến thiên suy ra phương trình đã cho có đúng hai nghiệm phân biệt thuộc $\large \left[\dfrac{1}{2}; 2\right]$ khi và chỉ khi $\large 2 < m \leq \dfrac{5}{2}$