Cho hình trụ có bán kính bằng R và chiều cao bằng $\large \dfrac{3R}{2

Cho hình trụ có bán kính bằng R và chiều cao bằng $\large \dfrac{3R}{2}$. Mặt phẳng $\large (\alpha)$ song song với trục của hình trụ và cách trục một khoảng bằng $\large \dfrac{R}{2}$. Diện tích thiết diện của hình trụ cắt bởi mặt phẳng $\large \alpha$ là: 

• A. $\large \dfrac{3\sqrt{2}.R^2}{2}$
• B. $\large \dfrac{3\sqrt{3}.R^2}{2}$
• C. $\large \dfrac{2\sqrt{3}.R^2}{3}$
• D. $\large \dfrac{2\sqrt{3}.R^2}{3}$

Chọn B

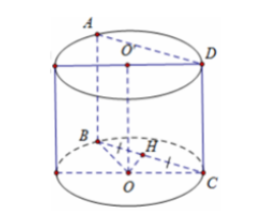
Giả sử thiết diện hình chữ nhật ABCD như hình vẽ

Gọi H là trung điểm của BC suy ra $\large OH\perp BC\Rightarrow d(O; BC) = \dfrac{R}{2}$

khi đó: $\large BC = 2HB= 2\sqrt{OB^2- OH^2} = 2\sqrt{ R^2 - \left(\dfrac{R}{2}\right)^2} = R\sqrt{3}$

Suy ra: $\large S_{ABCD} = BC.AB = R\sqrt{3}.\dfrac{3R}{2}= \dfrac{3\sqrt{3}.R^2}{2}$