Cho hình lập phương $\Large ABCD.{A}'{B}'{C}'{D}'$ có diện tích mặt ch

Cho hình lập phương $\Large ABCD.{A}'{B}'{C}'{D}'$ có diện tích mặt chéo $\Large AC{C}'{A}'$ bằng $\Large 2\sqrt{2}a^2$. Thể tích khối lập phương là

• A. $\Large 2\sqrt{2}a^3$.
• B. $\Large 8a^3$.
• C. $\Large \sqrt[4]{8^3}a^3$.
• D. $\Large a^3$.

Chọn A

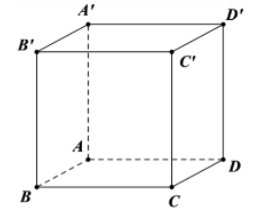
Gọi $\Large x$ là cạnh của hình lập phương $\Large \Rightarrow ABCD$ là hình vuông $\Large \Rightarrow AC=x\sqrt{2}$.

Do $\Large AC{C}'{A}'$ là hình chữ nhật nên $\Large S_{ABCD}=AC.A{A}'=x^2\sqrt{2}$ $\Large \Rightarrow x^2\sqrt{2}=2\sqrt{2}a^2\Leftrightarrow x=a\sqrt{2}$.

Vậy thể tích khối lập phương là $\Large x^3=2a^3\sqrt{2}$.