Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc $\larg

Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc $\large BAD = 60^\circ$ . Đường thẳng SO vuông góc với mặt đáy (ABCD) và $\large SO = \dfrac{3a}{4}$ . Khoảng cách từ O đến mặt phẳng (SBC) bằng 

• A. $\large \dfrac{3a}{4}$ 
• B. $\large \dfrac{a}{3} $ 
• C. $\large \dfrac{a\sqrt{3}}{4}$ 
• D. $\large \dfrac{3a}{8}$ 

Chọn D

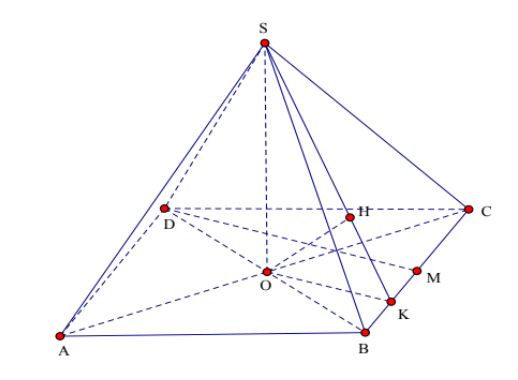
Ta có: Tứ giác ABCD là hình thoi cạnh a có $\large BAD= 60^\circ$  suy ra tam giác BCD là tam giác đều cạnh a

Gọi M là trung điểm cạnh BC. Suy ra: $\large DM\perp BC$  và $\large DM = \dfrac{a\sqrt{3}}{2}$ 

Kẻ $\large OK// DM,\, (K\in BC)\Rightarrow OK\perp BC$, $\large OK= \dfrac{1}{2}DM= \dfrac{a\sqrt{3}}{4}$ 

VÌ $\large SO\perp (ABCD)\Rightarrow BC\perp SO\Rightarrow BC\perp (SOK) $ 

Kẻ $\large OH\perp SK,\, (H\in SK)\Rightarrow OH\perp (SBC)$ 

Từ đó ta có: $\large d(O,\, (SBC)) = OH = \dfrac{OK.SO}{\sqrt{OK^2+ SO^2}} = \dfrac{\dfrac{a\sqrt{3}}{4}.\dfrac{3a}{4}}{\sqrt{\left(\dfrac{a\sqrt{3}}{4} \right )^2 + \left(\dfrac{3a}{4} \right )^2}}= \dfrac{3a}{8}$