Cho hàm số $\large y = f(x)$ có đạo hàm trên $\large \mathbb{R}$ và bả

Cho hàm số $\large y = f(x)$ có đạo hàm trên $\large \mathbb{R}$ và bảng xét dấu đạo hàm như hình vẽ sau: 

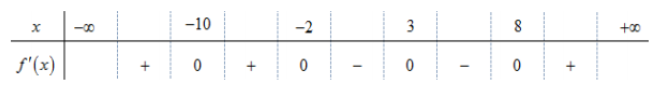
Có bao nhiêu số nguyên m để hàm số $\large y = f(x^3+ 4x+m)$ nghịch biến trên khoảng $\large (-1; 1)$?

• A. 3
• B. 0
• C. 1
• D. 2

Chọn C

Đặt $\large t = x^3+ 4x+m\Rightarrow t ' = 3x^2+ 4$ nên t đồng biến trên $\large (-1; 1)$ và $\large t\in (m-5; m+5)$

Yêu cầu bài toán trở thành tìm m để hàm số f(t) nghịch biến trên khoảng $\large (m-5; m+5)$

Dựa vào bảng biến thiên ta được: $\large \left\{\begin{align}& m- 5\geq -2\\& m+ 5\leq 8\\\end{align}\right. $ $\large \Leftrightarrow \left\{\begin{align}& m\geq 3\\& m\leq 3\\\end{align}\right. $ $\large \Leftrightarrow m= 3$